数学竞赛 梅涅劳斯定理

1
梅涅劳斯定理
梅涅劳斯(Menelaus )定理(简称梅氏定理)最早出现在由古希腊数学家梅涅劳斯的著作《球面学》(Sphaerica )。
任何一条直线截三角形的各边,都使得三条不相邻线段之积等于另外三条线段之积,这一定理同样可以轻而易举地用初等几何或通过应用简单的三角关系来证明. 梅涅劳斯把这一定理扩展到了球面三角形。
中文名 梅涅劳斯定理 外文名 Menelaus 别 称 梅氏定理
表达式
(AF/FB)×
(BD/DC)×(CE/EA)=1
提出者 梅涅劳斯
提出时间 1678年 应用学科 数学,物理 适用领域范围 平面几何学 适用领域范围 射影几何学
定理内容
定理证明
证明一
过点A 作AG ∥DF 交BC 的延长线于点G.则
证明二
过点C 作CP ∥DF 交AB 于P ,则
两式相乘得
2
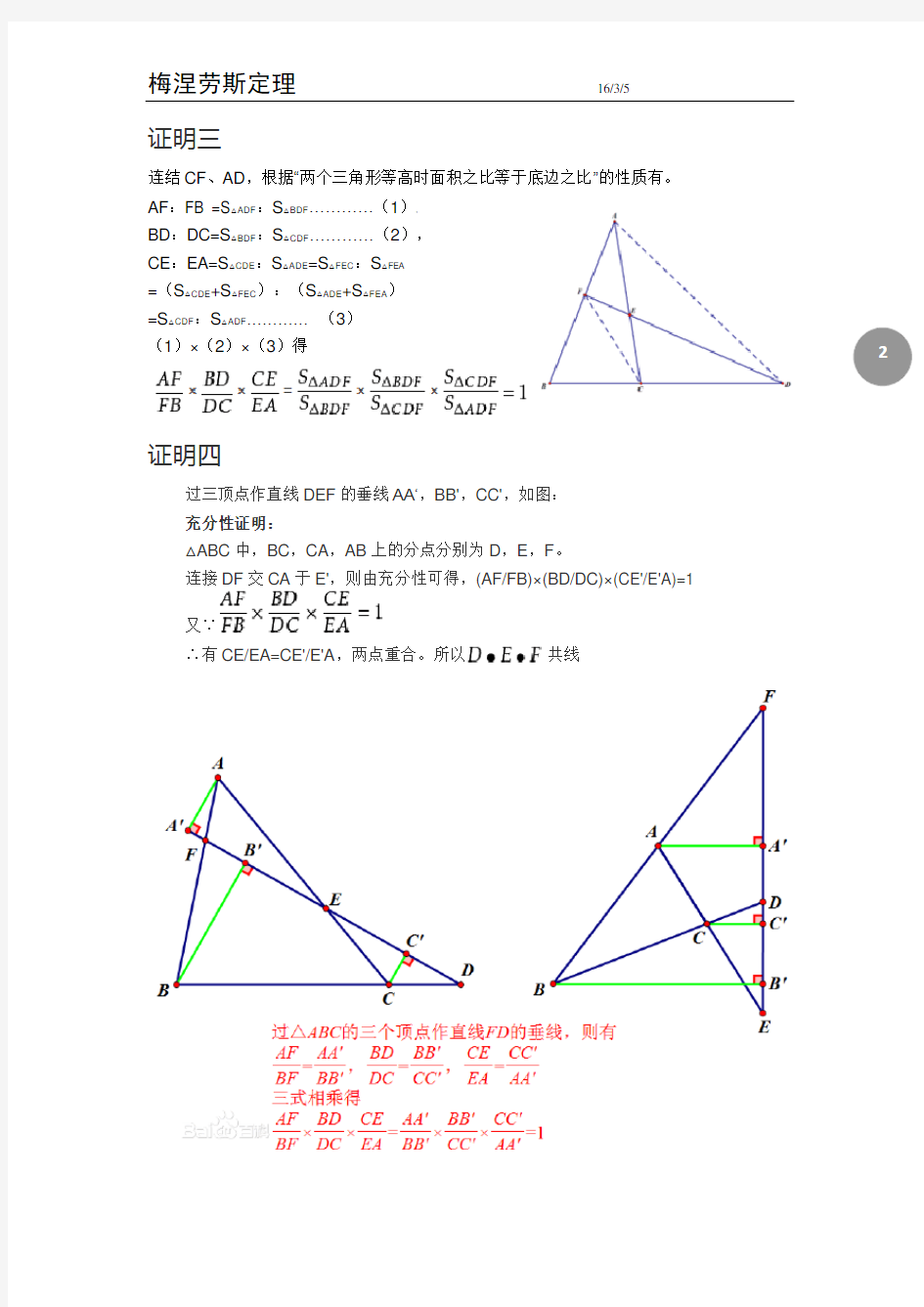
证明三
连结CF 、AD ,根据“两个三角形等高时面积之比等于底边之比”的性质有。 AF :FB =S △ADF :S △BDF …………(1), BD :DC=S △BDF :S △CDF …………(2), CE :EA=S △CDE :S △ADE =S △FEC :S △FEA =(S △CDE +S △FEC ):(
S △ADE +S △FEA
)
=S △CDF :S △ADF ………… (3) (1)×(2)×(3)得
证明四
过三顶点作直线DEF 的垂线AA…,BB',CC',如图: 充分性证明:
△ABC 中,BC ,CA ,AB 上的分点分别为D ,E ,F 。
连接DF 交CA 于E',则由充分性可得,(AF/FB)×(BD/DC)×(CE'/E'A)=1 又∵
∴有CE/EA=CE'/E'A ,两点重合。所以
共线
3
推论 在△ABC 的三边BC 、CA 、AB 或其延长线上分别取L 、M 、N 三点,又分比是λ=BL/LC 、μ=CM/MA 、ν=AN/NB 。于是AL 、BM 、CN 三线交于一点的充要条件是λμν=-1。(注意与塞瓦定理相区分,那里是λμν=1)
此外,用该定理可使其容易理解和记忆:
第一角元形式的梅涅劳斯定理如图:若E ,F ,D 三点共线,则 (sin ∠
ACF/sin ∠FCB)(sin ∠BAD/sin ∠DAC)(sin ∠CBE/sin ∠ABE)=1 即图中的蓝角正弦值之积等于红角正弦值之积。 该形式的梅涅劳斯定理也很实用。
证明:可用面积法推出:第一角元形式的梅氏定理与顶分顶形式的梅氏定理等价。 第二角元形式的梅涅劳斯定理
在平面上任取一点O ,且EDF 共线,则(sin ∠AOF/sin ∠FOB)(sin ∠BOD/sin ∠DOC)(sin ∠COE
/sin ∠AOE)=1。(O 不与点A 、B 、C 重合) 梅涅劳斯球面三角形定理
在球面三角形ABC 中,三边弧AB ,弧BC ,弧CA(都是大圆弧)被另一大圆弧截于P,Q,R 三点,那么
数学意义
使用梅涅劳斯定理可以进行直线形中线段长度比例的计算,其逆定理还可以用来解决三点共线、三线共点等问题的判定方法,是平面几何学以及射影几何学中的一项基本定理,具有重要的作用。梅涅劳斯定理的对偶定理是塞瓦定理。
它的逆定理也成立:若有三点F、D、E分别在的边AB、BC、CA或其延长线上,且
满足AF/FB×BD/DC×CE/EA=1,则F、D、E三点共线。利用这个逆定理,可以判断三点共
线。
4
梅涅劳斯逆定理
定理
若有三点F、D、E分别在边三角形的三边AB、BC、CA或其延长线上,且满足
AF/FB×BD/DC×CE/EA=1,则F、D、E三点共线。利用这个逆定理,可以判断三点共线。
注意定理中提到的三个点的位置,在梅涅劳斯逆定理中,三个点要么只有两个在三角
5
形边上,要么一个都不在三角形边上。
即:该逆定理成立的前提是三个点有偶数个点在三角形边上。
否则为塞瓦定理逆定理。
证明方式
已知:E、F是△ABC的边AB、AC上的点,D是BC的延长线的点,且有:
(AF/FB)(BD/DC)(CE/EA)=1。求证:E、F、D三点共线。思路:采用反证法。先假设E、F、
D三点不共线,直线DE与AB交于P。再证P与F重合。
证明:先假设E、F、D三点不共线,直线DE与AB交于P。
由梅涅劳斯定理的定理证明(如利用平行线分线段成比例的证明方法)得:
(AP/PB)(BD/DC)(CE/EA)=1。
∵(AF/FB)(BD/DC)(CE/EA)=1。
∴AP/PB=AF/FB ;
∴(AP+PB)/PB=(AF+FB)/FB ;
∴AB/PB=AB/FB ;
∴PB=FB;即P与F重合。
∴D、E、F三点共线。
注意
首先我们已知图中的直线关系:三角形一边的延长线上一点与相邻边上一点的连线与
另一边相交于一点,然后再来求各个边的关系。
梅涅劳斯的功劳在于,他根据上图的现象,发现了关系式:AF/FB×BD/DC×CE/EA=1
然后反过来再证明,如果满足这个关系,那么那条线是直线
总之:从现象发现等式,再从等式反推现象,这两个工作使得这一发现成为定理。
问题:
梅涅劳斯是怎么根据图中的现象发现或者计算出等式AF/FB×BD/DC×CE/EA=1 ?
这个问题请大家思考。
6
7
梅涅劳斯定理及例题拓展
梅涅劳斯介绍:在证明点共线时,有一个非常重要的定理,它就是梅涅劳斯定理,梅涅劳斯(Menelaus )是公元一世纪时的希腊数学家兼天文学家,著有几何学和三角学方面的许多书籍。下面的定理就是他首先发现的。这个定理在几何学上有很重要的应用价值。
定理:设D 、E 、F 依次是三角形ABC 的三边AB 、BC 、CA 或其延长线上的点,
且这三点共线,则满足
1=??FA
CF
EC BE DB AD 证明:(此定理需要分四种情况讨论,但有两种可以排除) 先来说明两种不可能的情况
情况一:当三点均在三角形边上时,由基本事实可知三点不可能共线(只能组成内接三角形的三角形。
情况二:当一点在三角形一边上,另两点分别在三角形另两边的延长线上时,如图是三角形ABC 直线DE 交AB 于点D ,交AC 于点F ,交BC 于点E ,平移直线DE 即可发现不能可两点同时在延长线上
情况三:当两点分别在三角形两边上,另一点在三角形另一边的延长线上时,如图是三角形ABC 直线DE 交AB 于点D ,交AC 于点F ,交BC 于点E ,
∵D 、E 、F 三点共线
∴可过C 作CM ∥DE 交AB 于M ,于是
FC
AF DM BD DM AD EC BE FC
AF
DM AD DM BD EC BE ?
=?∴==,,
所以
1=??FA
CF
EC BE DB AD 情况四:三点分别在三角形三边的延长线上时,如图是三角形ABC 直线DE 交AB 于点D ,交AC 于点F ,交BC 于点E ,
同情况三∵D 、E 、F 三点共线
∴可过C 作CM ∥DE 交AB 于M ,于是
FC
AF DM BD DM AD EC BE FC
AF
DM AD DM BD EC BE ?
=?∴==,,
所以
1=??FA
CF
EC BE DB AD
8
∴设D 、E 、F 依次是三角形ABC 的三边AB 、BC 、CA 或其延长线上的点,且
这三点共线,则满足
1=??FA
CF
EC BE DB AD
拓展 (1题)在任意三角形PQR 中,A2,A4分别是PR,PQ 延长线上的点,做射线A4A2,A6是射线A4A2上的一点,做射线A6Q ,A1是射线A6Q 上的一点,连结A1A2交射线PR 于X ,作射线A4A3交射线PQ 于点A3,交射线A1A6于点Y ,连结A1A3交射线PR 于点A5,连结A6A5交射线PQ 于点Z ,求证X,Y,Z 三点共线 (该命题又为一六边形相间各顶点分别在两直线上求证:它的三对对边(所在直线)的交点共线)这个定理为帕波斯定理
9
(2题)给定△ABC内两点O,O',连结AO,AO'交BC于点X,X',BO,BO'交AC于Y,Y',CO,CO'交AB于Z,Z'.设YZ'与Y'Z交于点P,ZX'与Z'X交于点Q,XY'与X'Y 交于点R.求证O,O',P,Q,R五点共线
(3题)在任意三角形ABC中,E是直线AC上的一点,D是直线BC上的一点,F 是直线DE上一点,G是直线AC上一点,作直线BG交直线DF于点Q,作直线CF 交直线AB于点P,作直线GF交直线AB于点H作直线DH交直线AC于点R,求证P,Q,R三点共线
10
(4题)一直线截△ABC三边BC,CA,AB或延长线X,Y,Z。证明:这三点的等截点X',Y',Z'共线。
(在三角形任意一边所在直线上,设有两点与此边的中点等距,则称这两个点互为等截点)
(5题)将一点与正三角形的顶点连线,
(1)若依次连结三联结线中点求证是个正三角形
(2)三联结线的中垂线分别与对边(所在直线)的交点共线
11
梅涅劳斯定理和塞瓦定理
一、 梅涅劳斯定理
定理1 若直线l 不经过?ABC 的顶点,并且与?ABC 的三边BC 、CA 、AB 或它们的延长线分别交于P 、Q 、R ,则
BP PC
?CQ QA
?AR RB
=1
证明:设?A 、?B 、?C 分别是A 、B 、C 到直线l 的垂线的长度,则:BP
PC ?CQ
QA ?AR
RB =
?B ?C
??C ?A
??
A ?B
=1。
注:此定理常运用求证三角形相似的过程中的线段成比例的条件。
例1 若直角?ABC 中,CK 是斜边上的高,CE 是∠ACK 的平分线,E 点在AK 上,D 是AC 的中点,F 是DE 与CK 的交点,证明:BF ∥CE 。
【解析】因为在?EBC 中,作∠B 的平分线BH ,则:∠EBC =∠ACK ,∠HBC =∠ACE ,∠HBC +∠HCB =∠ACK +∠HCB =90°,即BH ⊥CE ,所以?EBC 为等腰三角形,作BC 上的高EP ,则:CK =EP ,对于?ACK 和三点D 、E 、F 根据梅涅劳斯定理有:CD
DA ?AE
EK ?KF
FC =1,于是KF
FC =EK
AE =CK
AC =EP
AC =BP
BC =BK
BE ,即
KF FC
=
BK BE
,根据分比定理有:KF KC
=
BK KE
,所以?FKB ??CKE ,所以BF ∥CE 。
例2 从点K 引四条直线,另两条直线分别交直线与A 、B 、C 、D 和A 1,B 1,C 1,D 1,试证:
AC BC
:
AD BD
=
A 1C 1
B 1
C 1:A 1
D 1B 1D 1
。
【解析】若AD ∥A 1D 1,结论显然成立;若AD 与A 1D 1相交于点L ,则把梅涅劳斯定理分别用于?A 1AL 和?B 1BL 可得:
AD LD
?
LD 1A 1D 1
?
A 1K AK
=1,
LC AC ?AK A 1K ?A 1C 1LC 1=1,
BC LC
?
LC 1B 1C 1
?
B 1K BK
=1,LD BD
?
BK B 1K
?
B 1D 1LD 1
=1,将上面四个式子相乘,可得:AD AC
?
BC BD
?
A 1C 1
A 1D 1
?
B 1D 1B 1
C 1
=1,即:AC BC :
AD BD
=
A 1C 1
B 1
C 1:
B 1D 1B 1
C 1
定理2 设P 、Q 、R 分别是?ABC 的三边BC 、CA 、AB 上或它们延长线上的三点,并且P 、Q 、R 三点中,位于?ABC 边上的点的个数为0或2,这时若BP
PC ?CQ
QA ?AR
RB =1,求证P 、Q 、R 三点共线。
证明:设直线PQ 与直线AB 交于R ’,于是由定理1得:BP
PC ?CQ
QA ?AR ‘
R ’B =1,又因为BP
PC ?CQ
QA ?AR
RB =1,则
AR ‘R ’B
=AR
RB ,由于在同一直线上P 、Q 、R 三点中,位
于?ABC 边上的点的个数也为0或2,因此R 与R ‘或者同在AB 线段上,或者同在AB 的延长线上;若R 与R ‘同在AB 线段上,则R 与R ‘必定重合,不然的话,设AR >A R ‘,这时AB ?AR 即 BR ,于是可得 AR BR > AR ‘BR ‘,这与 AR BR = AR ‘BR ‘ 矛盾,类似地可证得当R 与R ‘同在AB 的延长线 上时,R 与R ‘也重合,综上可得:P 、Q 、R 三点共线。 注:此定理常用于证明三点共线的问题,且常需要多次使用 再相乘; 例3 点P 位于?ABC 的外接圆上;A 1、B 1、C 1是从点P 向BC 、CA 、AB 引的垂线的垂足,证明点A 1、B 1、C 1共线。 【解析】易得: BA 1CA 1 =? BP ?cos∠PBC CP ?cos∠PCB , CB 1AB 1 =? CP ?cos∠PCA AP ?cos∠PAC , AC 1BC 1 =?AP ?cos∠PAB BP ?cos∠PBA ,将上面三个式子相乘,且因为∠PCA =∠PBC , ∠PAB =∠PCB ,∠PCA +∠PBA =180°,可得BA 1CA 1 ?CB 1AB 1 ?AC 1BC 1 =1,根据梅涅劳斯定理可知A 1、B 1、C 1三点共线。 例4 设不等腰?ABC 的内切圆在三边BC 、CA 、AB 上的切点分别为D 、E 、F ,则EF 与BC ,FD 与CA ,DE 与AB 的交点X 、Y 、Z 在同一条直线上。 【解析】?ABC 被直线XFE 所截,由定理1可得:BX XC ?CE EA ?AF FB =1,又因为AE =AF ,代入上式可得BX XC =FB CE ,同理可得 CY YA = DC AF ,AZ ZB = EA BD , 将上面的式子相乘可得: BX XC ? CY YA ? AZ ZB =1,又因为X 、Y 、Z 丢不 在?ABC 的边上,由定理2可得X 、Y 、Z 三点共线。 例5 已知直线AA 1,BB 1,CC 1相交于O ,直线AB 和A 1B 1的交点为C 2,直线BC 和B 1C 1的交点为A 2,直线AC 和A 1C 1的交点为B 2,试证A 2、B 2、C 2三点共线。 【解析】设A 2、B 2、C 2分别是直线BC 和B 1C 1,AC 和A 1C 1,AB 和A 1B 1的交点,对所得的三角形和它们边上的点:OAB 和(A 1,B 1,C 2),OBC 和(B 1,C 1,A 2),OAC 和(A 1,C 1,B 2)应用梅涅劳斯定理有: AA 1OA 1 ? OB 1BB 1 ? BC 2AC 2 =1, OC 1CC 1 ? BB 1OB 1 ? CA 2BA 2 =1, OA 1AA 1 ? CC 1OC 1 ? AB 2CB 2 =1,将上面的三 个式子相乘,可得:BC 2AC 2 ?AB 2CB 2 ?CA 2BA 2 =1,由梅涅劳斯定理可知A 2、B 2、C 2 共线。 例6 在一条直线上取点E 、C 、A ,在另一条上取点B 、F 、D ,记直线AB 和ED ,CD 和AF ,EF 和BC 的交点依次为L 、M 、N ,证明:L 、M 、N 共线。 【解析】记直线EF 和CD ,EF 和AB ,AB 和CD 的交点分别为U 、V 、W ,对?UVW ,应用梅涅劳斯定理于五组三元点(L,D,E),(A,M,F),(B,C,N),(A,C,E),(B,D,F),则有UE VE ?VL WL ? WD UD =1, VA WA ?UF VF ? WM YM =1,UN VN ? WC UC ?VB WB =1,WA VA ?UC WC ?VE UE =1,WB VB ?UD WD ?VF UF =1,将上面五个式子相乘 可得:VL WL ? WM UM ?UN VN =1,点L 、M 、N 共线。 13 二、塞瓦定理 定理:设P 、Q 、R 分别是?ABC 的BC 、CA 、AB 边上的点,则AP 、BQ 、CR 三线共点的充要条件是: BP PC ? CQ QA ? AR RB =1。 证明:先证必要性:设AP 、BQ 、CR 相交于点M ,则 BP PC =S ?ABP S ?ACP =S ?BMP S ?CMP =S ?ABM S ?ACM ,同理CQ QA =S ?BCM S ?ABM ,AR RB =S ?ACM S ?BCM ,以 上三式相乘,得:BP PC ? CQ QA ? AR RB =1,再证充分性:若 BP PC ? CQ QA ? AR RB =1 设AP 与BQ 相交于M ,且直线CM 交AB 于R ’,由塞瓦定理有: BP PC ?CQ QA ?AR ’R ’B =1,约翰斯:AR ’ R ’B =AR RB ,因为R 和R ’ 都在线段 AB 上,所以R ’必与R 重合,故AP 、BQ 、CR 相交于一点M 。 例7 证明:三角形的中线交于一点。 【解析】记?ABC 的中线AA 1,BB 1,CC 1,我们只须证明 AC 1C 1 B ?BA 1 A 1 C ?CB 1 B 1A =1,而显然有:AC 1=C 1B ,BA 1=A 1C , CB 1= B 1A ,即AC 1 C 1 B ?BA 1 A 1 C ?CB 1 B 1A =1成立,所以,?ABC 交于一点, 例8 在锐角?ABC 中,∠C 的角平分线交AB 于L ,从L 做边AC 和BC 的垂线,垂足分别是M 和N ,设AN 和BM 的交点是P ,证明:CP ⊥AB 。 【解析】作CK ⊥AB ,下证CK 、BM 、AN 三线共点,且为P 点,要证CK 、BM 、AN 三线共点,根据塞瓦定理即要证:AM MC ?CN NB ?BK AK =1,又因为MC =CN ,即要证明:AM AK ?BK NB =1,因为?AML ??AKC ? AM AK =AL AC , ?BNL ??BKC ?BK NB =BC BL ,即要证AL AC ?BC BL =1,根据三 角形的角平分线定理可知:AL AC ?BC BL =1,所以CK 、BM 、AN 三线共点,且为P 点,所以CP ⊥AB 。 例9 设AD 是?ABC 的高,且D 在BC 边上,若P 是AD 上任一点,BP 、CP 分别与AC 、AB 交于E 和F ,则∠EDA =∠FDA 。 【解析】过A 作AD 的垂线,与DE 、DF 的延长线分别交于M 、N 。欲证∠EDA =∠FDA ,可以转化为证明AM =AN ,因为AD ⊥BC ,故MN ∥BC ,可得?AME ??CDE ,?ANF ??BDF ,所以AM CD =AE CE ,AN BD = AF BF ,于是AM =AE ?CD CE ,AN = AF ?BD BF ,因为AD 、BE 、CF 共点与P ,根 据塞瓦定理可得:BD DC ?CE EA ?AF FB =1,所以AE ?CD CE = AF ?BD BF ,所以 AM =AN ,所以∠EDA =∠FDA 例10在?ABC的边BC、CA、AB上取点A1、B1、C1,证明 AC1 C1B ?BA1 A1C ?CB1 B1A =sin∠AC C1 sin∠C1CB ?sin∠BA A1 sin∠A1AC ?sin∠CB B1 sin∠B1BA 【解析】如图对?ACC1和?BCC1应用正弦定理,可得 AC1 C1C =sin∠AC C1 sin∠A ,CC1 C1B =sin∠B sin∠C1CB ,即AC1 C1B =sin∠AC C1 sin∠C1CB ?sin∠B sin∠A ,同理: BA1 A1C =sin∠BA A1 sin∠A1AC ?sin∠C sin∠B ,CB1 B1A =sin∠CB B1 sin∠B1BA ?sin∠A sin∠C ,从而AC1 C1B ?BA1 A1C ? CB1 B1A =sin∠AC C1 sin∠C1CB ?sin∠BA A1 sin∠A1AC ?sin∠CB B1 sin∠B1BA 。 14 梅涅劳斯定理范文 梅涅劳斯定理 定理叙述 设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z 共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1 注意: 最简单的证明(张景中院士说过“做足够多的三角形可以解任何几何题”。等价说法是“做足够多的垂线可以解任何几何题”)证明:过ABC三点向三边引垂线AA'BB'CC', AD:DB=AA':BB' BE:EC=BB':CC' CF:FA=CC':AA' 所以(AF/FB)×(BD/DC)×(CE/EA)=1 一应用梅涅劳斯定理 1.定理的条件已经具备,正向或反向应用定理。 例:过三角形外接圆上异于三角形顶点的任意一点作三边的垂线,则三垂足共线。(此线常称为西姆松线)。分析:目标明确,写出比例式就行了。 例:不等边三角形的三条外角平分线与对边延长线的交点共线。 例: 分析:直线若平行于BC,则命题显然成立。若不平行,则作出直线与直线BC的交点是非常自然的。 例: 如图在三角形三边取相同比例的分点。中间黑色三角形面积等于白色面积,求边上的分点比例。 分析:没啥好分析的。 总结:用定理要选取三角形和截线。目标中共线的三个点所在的直线上,一般不会包含所选取的三角形的边。 2.几个不适合用梅氏定理的例子。 例: 如图锐角x的两条边上取A,B两点。甲乙二人分别从A,B出发沿箭头方向前进。保持速度不变。证明两人以及锐角顶点组成的三角形垂心在某直线上运动。分析:本题具备定理的基本图形,并且目标是证明共线。但此处不可使用梅氏定理。因为垂心所在的定直线一般是不过锐角顶点的。那么我们取几个时刻的垂心呢?两个就够了。只要证明这两个垂心连线的斜率只与两人的速度比有关…… 总结:用数学定理要看定理中的条件部分,估计计算复杂程度。比如逆定理条件是共线,不共线则不可使用逆定理。 例: 两个线段上的点列如图连线得到交点。证明三个交点共线。用梅氏定理的证明见初三仁华课本。这里绕个路证明此题。首先,下面这个事实有用。 x,y,z,w等8个数看作所在点横坐标。(用了定比分点) 第一章涅劳斯定理及应用 【基础知识】 梅涅劳斯定理 设A ',B ',C '分别是ABC △的三边BC ,CA ,AB 或其延长线上的点,若A ',B ', C '三点共线,则1BA CB AC A B B A C B ''' ??='''. ① C ′ B′ A' A′ B′ C ′ A C B D C B 图1-1 A 证明 如图11-,过A 作直线AD C A ''∥交BC 的延长线于D ,则 CB CA B A A D ''='',AC DA C B A B '' = '',故 1BA CB AC BA CA DA A C B A C B A C A D A B '''''' ??=??=''''''. 注 此定理的证明还有如下正弦定理证法及面积证法. 正弦定理证法 设BC A α''=∠,CB A β''=∠,B A B γ''=∠,在BA C ''△中,有 sin sin BA C B α γ '= ',同理,sin sin CB CA γβ'=',sin sin AC AB β α '= ',此三式相乘即证. 面积证法 由A C B A C C S BA A C S '''''='△△,CB C CA B CB C CA B C CA B AC A AB B AC A AB AC A S S S S S CB B A S S S S S ''''''''''''''''''''+===='+△△△△△△△△△△,AC A C BA S AC C B S '' '' '= '△△,此三式相乘即证. 梅涅劳斯定理的逆定理 设A ',B ',C '分别是ABC △的三边BC ,CA ,AB 或其延长线上的点,若 1BA CB AC A C B A C B ''' ??=''', ② 则A ',B ',C '三点共线. 证明 设直线A B ''交AB 于1C ,则由梅涅劳斯定理,得到1 11AC BA CB A C B A C A ''??=''. 由题设,有1BA CB AC A C B A C B ''' ??=''',即有 11AC AC C B C B '='. 又由合比定理,知 1AC AC AB AB ' = ,故有1AC AC '=,从而1C 与C '重合,即A ',B ',C '三点共线. 有时,也把上述两个定理合写为:设A ',B ',C '分别是ABC △的三边BC ,CA ,AB 所在直线(包括三边的延长线)上的点,则A ',B ',C '三点共线的充要条件是 1BA CB AC A C B A C B ''' ??='''. 上述①与②式是针对ABC △而言的,如图11-(整个图中有4个三角形),对于C BA ''△、B CA ''△、AC B ''△也有下述形式的充要条件: 梅涅劳斯定理 定理叙述 设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1 注意: 1 定理的应用有正反两个方向。由共线推出比例式叫作逆定理。 2 三个分点可能有两个在线段上,或者三个都不在线段上。 最简单的证明(张景中院士说过“做足够多的三角形可以解任何几何题”。等价说法是“做足够多的垂线可以解任何几何题”) 证明:过ABC三点向三边引垂线AA'BB'CC', AD:DB=AA':BB' BE:EC=BB':CC' CF:FA=CC':AA' 所以(AF/FB)×(BD/DC)×(CE/EA)=1 一应用梅涅劳斯定理 1.定理的条件已经具备,正向或反向应用定理。 例:过三角形外接圆上异于三角形顶点的任意一点作三边的垂线,则三垂足共线。(此线常称为西姆松线)。 分析:目标明确,写出比例式就行了。 例:不等边三角形的三条外角平分线与对边延长线的交点共线。 分析:此题同上。注意外角平分线分对边成的比例与夹边比例的关系,是和内角平分线类似的。 例: 分析:直线若平行于BC,则命题显然成立。若不平行,则作出直线与直线BC的交点是非常自然的。 例: 如图在三角形三边取相同比例的分点。中间黑色三角形面积等于白色面积,求边上的分点比例。 分析:没啥好分析的。 总结:用定理要选取三角形和截线。目标中共线的三个点所在的直线上,一般不会包含所选取的三角形的边。 2.几个不适合用梅氏定理的例子。 例: 如图锐角x的两条边上取A,B两点。甲乙二人分别从A,B出发沿箭头方向前进。保持速度不变。证明两人以及锐角顶点组成的三角形垂心在某直线上运动。 分析:本题具备定理的基本图形,并且目标是证明共线。但此处不可使用梅氏定理。因为垂心所在的定直线一般是不过锐角顶点的。那么我们取几个时刻的垂心呢?两个就够了。只要证明这两个垂心连线的斜率只与两人的速度比有关…… 梅涅劳斯定理(入门篇) 雷雨田 (广西师范大学附属外国语学校高50班 541004) 梅涅劳斯定理 这个定理怎么记最好呢? 个人感觉“顶到分、分到顶、顶到分、分到顶、顶到分、分到顶”这样记忆来得非常容易 不过找了很多资料,感觉仅仅是把这个定理(或者后面附一个逆定理)陈述然后证明完了之后,就直接给例题(或者直接讲赛瓦定理),看上去不怎么舒服,所以我把其他的一些东西附在这里,以供参考。 第一角元形式的梅涅劳斯定理 (就是把线段比改为正弦值比)其表达式为: 1=∠∠?∠∠?∠∠BA 'B sin 'CBB sin CB 'C sin 'ACC sin AC 'A sin 'BAA sin 证明如下: 如图所示,由三角形面积公式(正弦定理)可得: AC 'A sin AC 'BAA sin AB AC 'A sin AC 'AA 'BAA sin 'AA AB S S C 'A 'BA C 'AA 'ABA ∠?∠?=∠??∠??==??2 121 同理可得CB 'C sin BC 'ACC sin AC B 'C 'AC ,BA 'B sin AB 'CBB sin BC A 'B 'CB ∠?∠?=∠?∠?= 把这三个式子相乘,运用梅氏定理,就可得到 这个式子怎么记最好呢? 个人感觉根据梅涅劳斯定理中线段所对应的角来记忆最好。 第二角元形式的梅涅劳斯定理 设O 是不在三角形ABC 三边所在直线上的任意一点,其他条件不变,则表达式为: 1=∠∠?∠∠?∠∠OA 'B sin 'COB sin OB 'C sin 'AOC sin OC 'A sin 'BOA sin 现证明如下: B C A’ 1 梅涅劳斯定理 梅涅劳斯(Menelaus )定理(简称梅氏定理)最早出现在由古希腊数学家梅涅劳斯的著作《球面学》(Sphaerica )。 任何一条直线截三角形的各边,都使得三条不相邻线段之积等于另外三条线段之积,这一定理同样可以轻而易举地用初等几何或通过应用简单的三角关系来证明. 梅涅劳斯把这一定理扩展到了球面三角形。 中文名 梅涅劳斯定理 外文名 Menelaus 别 称 梅氏定理 表达式 (AF/FB)× (BD/DC)×(CE/EA)=1 提出者 梅涅劳斯 提出时间 1678年 应用学科 数学,物理 适用领域范围 平面几何学 适用领域范围 射影几何学 定理内容 定理证明 证明一 过点A 作AG ∥DF 交BC 的延长线于点G.则 证明二 过点C 作CP ∥DF 交AB 于P ,则 两式相乘得 2 证明三 连结CF 、AD ,根据“两个三角形等高时面积之比等于底边之比”的性质有。 AF :FB =S △ADF :S △BDF …………(1), BD :DC=S △BDF :S △CDF …………(2), CE :EA=S △CDE :S △ADE =S △FEC :S △FEA =(S △CDE +S △FEC ):( S △ADE +S △FEA ) =S △CDF :S △ADF ………… (3) (1)×(2)×(3)得 证明四 过三顶点作直线DEF 的垂线AA…,BB',CC',如图: 充分性证明: △ABC 中,BC ,CA ,AB 上的分点分别为D ,E ,F 。 连接DF 交CA 于E',则由充分性可得,(AF/FB)×(BD/DC)×(CE'/E'A)=1 又∵ ∴有CE/EA=CE'/E'A ,两点重合。所以 共线 板块一 梅涅劳斯定理及其逆定理 知识导航 梅涅劳斯定理:如果一条直线与ABC △的三边AB 、BC 、CA 或其延长线交于F 、D 、E 点, 那么1AF BD CE FB DC EA ??=.这条直线叫ABC △的梅氏线,ABC △叫梅氏三角形. G F E D C B A G F E D C B A H 3H 2 H 1 F E D C B A 证法一:如左图,过C 作CG ∥DF ∵DB FB DC FG =,EC FG AE AF = ∴1AF BD CE AF FB FG FB DC EA FB FG AF ??=??=. 证法二:如中图,过A 作AG BD ∥交DF 的延长线于G ∴AF AG FB BD =,BD BD DC DC =,CE DC EA AG = 三式相乘即得:1AF BD CE AG BD DC FB DC EA BD DC AG ??=??=. 证法三:如右图,分别过A B C 、、作DE 的垂线,分别交于123H H H 、 、. 则有123AH BH CH ∥∥, 所以3 12231 1CH AH BH AF BD CE FB DC EA BH CH AH ??=??=. 梅涅劳斯定理的逆定理:若F 、D 、E 分别是ABC △的三边AB 、BC 、CA 或其延长线的三点, 如果1AF BD CE FB DC EA ??=,则F 、D 、E 三点共线. 梅涅劳斯定理与塞瓦定理 夯实基础 【例1】 如图,在ABC △中,AD 为中线,过点C 任作一直线交AB 于点F ,交AD 于点E ,求 证::2:AE ED AF FB =. E C D B F A 【解析】 ∵直线FEC 是ABD △的梅氏线, ∴1AE DC BF ED BC FA ??=. 而12DC BC =,∴112AE BF ED FA ??=,即2AE AF ED BF =. 习题1. 在△ABC 中,D 是BC 的中点,经过点D 的直线交AB 于点E ,交CA 的延长线于点 F .求证: FA EA FC EB =. E F B D C A 【解析】 直线截ABC △三边于D 、E 、F 三点,应用梅氏定理,知 1CD BE AF DB EA FC ??=,又因为BD BC =,所以 1BE AF EA FC ?=,即FA EA FC EB = . 习题2. 如图,在△ABC 中, 90ACB ∠=?,AC BC =.AM 为BC 边上的中线, CD AM ⊥于点D ,CD 的延长线交AB 于点E .求AE EB . D E B M C A 【解析】 由题设,在Rt AMC △中,CD AM ⊥,2AC CM =, 平面几何问题:1.梅涅劳斯定理 一直线分别截△ABC的边BC、CA、AB(或其延长线)于D、E、F,则1 FB AF EA CE DC BD = ? ?。 背景简介:梅涅劳斯(Menelaus)定理是由古希腊数学家梅涅劳斯首先证明的。 证明: 说明: (1)结论的图形应考虑直线与三角形三边交点的位置情况,因而本题图形应该有两个。 (2)结论的结构是三角形三边上的6条线段的比,首尾相连,组成一个比值为1的等式。 (3)梅氏定理及其逆定理不仅可以用来证明点共线问题,而且是解决许多比例线段问题的有力 工具。用梅氏定理求某个比值的关键,在于恰当地选取梅氏三角形和梅氏线。 梅涅劳斯定理的逆定理:如果有三点F、D、E分别在△ABC的三边AB、BC、CA或其延长线上, 且满足1 EA CE DC BD FB AF = ? ?,那么F、D、E三点共线。 利用梅涅劳斯定理的逆定理可判定三点共线。 梅涅劳斯定理练习 1.设AD是△ABC的边BC上的中线,直线CF交AD于F。求证: FB AF 2 ED AE =。 2.过△ABC 的重心G 的直线分别交AB 、 AC 于E 、F ,交CB 延长线于D 。求证: 1FA CF EA BE =+。 3. 在△ABC 中,点D 在BC 上,31DC BD =,分别在AB ,AD 上,32EB AE =,2 1 GD AG =,EG 交 AC 于点F ,求 FC AF 。 4.在□ABCD 中,E ,F 分别是AB ,BC 的中点,AF 与CE 相交于G ,AF 与DE 交于H ,求AH:HG:GF 5.设D 为等腰Rt △ABC (∠C=90°)的直角边BC 的中点,E 在AB 上,且AE :EB=2:1, 求证:CE ⊥AD 6.在△ABC 中,点M 和N 顺次三等分AC ,点X 和Y 顺次三等分BC ,AY 与BM ,BN 分别交于点S ,R ,求四边形SRNM 与△ABC 的面积之比。 梅涅劳斯定理 【定理内容】 如果一条直线与ABC ?的三边AB 、BC 、CA 或其延长线交于F 、D 、E 点, 那么 1=??EA CE DC BD FB AF . [评]等价叙述:ABC ?的三边AB 、BC 、CA 或其延长线上有三点F 、D 、E , 则F 、D 、E 三点共线的充要条件是 1=??EA CE DC BD FB AF 。三点所在直线称为三角形的梅氏线。 【背景简介】 梅涅劳斯(Menelaus )定理是由古希腊数学家梅涅劳斯首先证明的。 【证法欣赏】 证法1:(平行线分线段成比例) 证:如图,过A 作BC AG //交CF 延长线于G , ∵BC AG //,∴BD AG FB AF =,AG CD EA CE =, 又 CD BD CD BD = B G 则 1=??=??CD BD AG CD BD AG CD BD EA CE FB AF ∴1=??EA CE DC BD FB AF 证法2:(正弦定理) 证:如图,令α=∠AEF ,β=∠AFE ,γ=∠BDE , 在AEF ?中,由正弦定理知: β αsin sin AE AF =, 同理 ββγsin )180sin(sin BD BD BF =-?=,γ αsin sin CE CD = ∴βαsin sin =AE AF ,γβsin sin =BF BD ,α γsin sin =CD CE , ∴ 1=??CD CE BF BD AE AF ,即1=??EA CE DC BD FB AF . 【逆定理】 梅涅劳斯定理的逆定理也成立,即 如果有三点F 、D 、E 分别在ABC ?的三边AB 、BC 、CA 或其延长线上,且满足 1=??EA CE DC BD FB AF ,那么F 、D 、E 三点共线。 [注]利用梅涅劳斯定理的逆定理可判定三点共线 B 梅涅劳斯定理及应用 定理:设Z Y X ,,分别是ABC ?的边AB CA BC ,,或其延长线的点,则Z Y X ,,三点共线的充要条件是: 1=??ZB AZ YA CY XC BX 例1:在O B C ?中,A 为BC 的中点,D 为OB 上的点,且21=OD BD ,E CD OA 相交于点与,则OA OE _____= 例2:如图,过ABC ?的三个顶点C B A ,,作它的外接圆的切线,分别和BA CA BC ,,的延长线交于R Q P ,,;求证:R Q P ,,三点共线 例3:(1985年第三届美国数学邀请赛)如图,G 是ABC ?内一点,直线CG BG AG ,,将ABC ?分为6个小三角形,已知BDG BFG AFG ???,,的面积分别为40,30,35,求A B C ?的 面积 例4: (1983年全国高中数学联赛)在四边形ABCD 中,ABC BCD ABD ???,,的面积之比是1:4:3,点M,N 分别在AC,CD 上,满足AM:AC=CN:CD ,并且B,M,N 三点共线,求证M 与N 分别是AC 和CD 的中点 练习:1(2009年中国科技大学)已知ABC ?的面积为1,;F E D ,,分别在边AB CA BC ,,上,FB AF EA CE DC BD 2,2,2===;CF BE AD ,,两两交于R Q P ,,,求PQR ?的面积 2 四边形ABCD (不是正方形)的内切圆分别切DA CD BC AB ,,,于H G F E ,,,,求证:GF DB HE ,,三线共点 3 (1982年第23届IMO 试题)已知CE AC ,是正六边形ABCDEF 的两条对角线,点N M ,分别在线段CE AC ,上,且使 k CE CN AC AM ==,如果N M B ,,三点共线,试求k 的值 4(2016年湖南省高中数学夏令营):ABC ?的内切圆分别与BC 、CA 、 AB 相切于点D 、E 、F,直线AD 与EF 相交于点H ,若直线BC EF 与相交于点G ,求证:GE FG HE FH = 梅涅劳斯定理 简介 梅涅劳斯(Menelaus)定理(简称梅氏定理)是由古希腊数学家梅涅劳斯首先证明的。它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。 或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1 证明一: 过点A作AG∥BC交DF的延长线于G, 则AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG。 三式相乘得:(AF/FB)×(BD/DC)×(CE/EA)=(AG/BD)×(BD/DC)×(DC/AG)=1 证明二: 过点C作CP∥DF交AB于P,则BD/DC=FB/PF,CE/EA=PF/AF 所以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=1 它的逆定理也成立:若有三点F、D、E分别在△ABC的边AB、BC、CA或其延长线上,且满足(AF/FB)×(BD/DC)×(CE/EA)=1,则F、D、E三点共线。利用这个逆定理,可以判断三点共线。 梅涅劳斯(Menelaus)定理 证明三: 过ABC三点向三边引垂线AA'BB'CC', 所以AD:DB=AA':BB',BE:EC=BB':CC',CF:FA=CC':AA' 所以(AF/FB)×(BD/DC)×(CE/EA)=1 此外,用定比分点定义该定理可使其容易理解和记忆: 在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点,又分比是λ=BL/ LC、μ=CM/MA、ν=AN/NB。于是L、M、N三点共线的充要条件是λμν=-1。(注意与塞瓦定理相区分,那里是λμν=1) 记忆 ABC为三个顶点,DEF为三个分点 (AF/FB)×(BD/DC)×(CE/EA)=1 (顶到分/分到顶)*(顶到分/分到顶)*(顶到分/分到顶)=1 空间感好的人可以这么记:(上1/下1)*(整/右)*(下2/上2)=1 实际应用 为了说明问题,并给大家一个深刻印象,我们假定图中的A、B、C、D、E、F 是六个旅游景点,各景点之间有公路相连。我们乘直升机飞到这些景点的上空,然后选择其中的任意一个景点降落。我们换乘汽车沿公路去每一个景点游玩,最后回到出发点,直升机就停在那里等待我们回去。 我们不必考虑怎样走路程最短,只要求必须“游历”了所有的景点。只“路过”而不停留观赏的景点,不能算是“游历”。 例如直升机降落在A点,我们从A点出发,“游历”了其它五个字母所代表的景点后,最终还要回到出发点A。 另外还有一个要求,就是同一直线上的三个景点,必须连续游过之后,才能变更到其它直线上的景点。 从A点出发的旅游方案共有四种,下面逐一说明: 方案①——从A经过B(不停留)到F(停留),再返回B(停留),再到D(停留),之后经过B(不停留)到C(停留),再到E(停留),最后从E经过C(不停留)回到出发点A。 按照这个方案,可以写出关系式: (AF:FB)*(BD:DC)*(CE:EA)=1。 现在,您知道应该怎样写“梅涅劳斯定理”的公式了吧。 从A点出发的旅游方案还有: 方案②——可以简记为:A→B→F→D→E→C→A,由此可写出以下公式:(AB:BF)*(FD:DE)*(EC:CA)=1。从A出发还可以向“C”方向走,于是有: 平面几何问题: 1.梅涅劳斯定理 一直线分别截△ABC 的边BC 、CA 、AB (或其延长线)于D 、E 、F ,则1FB AF EA CE DC BD =??。 背景简介:梅涅劳斯(Menelaus )定理是由古希腊数学家梅涅劳斯首先证明的。 证明: 说明: (1)结论的图形应考虑直线与三角形三边交点的位置情况,因而本题图形应该有两个。 (2)结论的结构是三角形三边上的6条线段的比,首尾相连,组成一个比值为1的等式。 (3)梅氏定理及其逆定理不仅可以用来证明点共线问题,而且是解决许多比例线段问题的有力工具。用梅氏定理求某个比值的关键,在于恰当地选取梅氏三角形和梅氏线。 梅涅劳斯定理的逆定理:如果有三点F 、D 、E 分别在△ABC 的三边AB 、BC 、CA 或其延长线上,且满足 1EA CE DC BD FB AF =??,那么F 、D 、E 三点共线。 利用梅涅劳斯定理的逆定理可判定三点共线。 梅涅劳斯定理练习 1.设AD 是△ABC 的边BC 上的中线,直线CF 交AD 于F 。求证: FB AF 2ED AE = 。 2.过△ABC 的重心G 的直线分别交AB 、AC 于E 、F ,交CB 延长线于D 。求证: 1FA CF EA BE =+。 3.在△ABC 中,点D 在BC 上,31DC BD =,分别在AB ,AD 上,32EB AE =,2 1 GD AG =,EG 交AC 于点F ,求 FC AF 。 4.在□ABCD 中,E ,F 分别是AB ,BC 的中点,AF 与CE 相交于G ,AF 与DE 交于H ,求 AH:HG:GF 5.设D 为等腰Rt △ABC (∠C=90°)的直角边BC 的中点,E 在AB 上,且AE :EB=2:1, 求证:CE ⊥ AD 6.在△ABC 中,点M 和N 顺次三等分AC ,点X 和Y 顺次三等分BC ,AY 与BM ,BN 分别交于点S ,R ,求四边形SRNM 与△ABC 的面积之比。 梅涅劳斯定理及例题拓展 梅涅劳斯介绍:在证明点共线时,有一个非常重要的定理,它就是梅涅劳斯定理,梅涅劳斯(Me nel aus)是公元一世纪时的希腊数学家兼天文学家,著有几何学和三角学方面的许多书籍。下面的定理就是他首先发现的。这个定理在几何学上有很重要的应用价值。 定理:设D 、E 、F依次是三角形ABC 的三边AB、BC 、CA 或其延长线上的 点,且这三点共线,则满足1=??FA CF EC BE DB AD 证明:(此定理需要分四种情况讨论,但有两种可以排除) 先来说明两种不可能的情况 情况一:当三点均在三角形边上时,由基本事实可知三点不可能共线(只能组成内接三角形的三角形。 情况二:当一点在三角形一边上,另两点分别在三角形另两边的延长线上时,如图是三角形ABC 直线DE 交AB 于点D ,交A C于点F,交BC 于点E,平移直线D E即可发现不能可两点同时在延长线上 情况三:当两点分别在三角形两边上,另一点在三角形另一边的延长线上时,如图是三角形AB C直线DE 交A B于点D,交AC 于点F ,交BC 于点E , ∵D 、E 、F三点共线 ∴可过C作CM ∥D E交AB 于M ,于是 FC AF DM BD DM AD EC BE FC AF DM AD DM BD EC BE ?=?∴==,, 所以1=??FA CF EC BE DB AD 情况四:三点分别在三角形三边的延长线上时,如图是三角形ABC 直线D E交AB 于点D,交AC 于点F ,交BC 于点E, 同情况三∵D 、E 、F 三点共线 ∴可过C 作CM ∥DE 交A B于M,于是 FC AF DM BD DM AD EC BE FC AF DM AD DM BD EC BE ?=?∴==,, 所以1=??FA CF EC BE DB AD 梅涅劳斯定理: 1l ABC ABC BC CA AB BP P Q R 1PC CQ AR QA RB ????=定理:若直线不经过的顶点,并且与的三边、、或它们的延长线分别交于、、,则 1 A B C C B A C A B h h h A B C l h h h BP CQ AR PC QA RB h h h ??=??=证:设、、分别是、、到直线的垂线的长度,则: 注:此定理常运用求证三角形相似的过程中的线段成比例的条件; 1//ABC CK CE ACK E AK D AC F DE CK BF CE ?∠例:若直角中,是斜边上的高,是的平分线,点在上,是的中点,是与的交点,证明:。 ,901EBC B BH EBC ACK HBC ACE HBC HCB ACE HCB BH CE EBC BC EP CK EP CD AE KF ACK D E F DA EK FC KF EK CK EP BP BK KF BK FC AE AC AC BC BE FC BE KF BK FKB KC KE ?∠∠=∠∠=∠∠+∠=∠+∠=? ⊥∴?=???=====∴??证:在中,作的平分线则:即:为等腰三角形作上的高,则:对于和三点、、依梅涅劳斯定理有:于是=即:= 依分比定理有://CKE BF CE ?∴ 2P Q R ABC BC CA AB P Q R ABC BP 021PC P Q R CQ AR QA RB ????=定理:设、、分别是的三边、、上或它们的延长线上的三点,并且、、三点中,位于边上的点的个数为或,这时若, 求证:、、三点共线; '' ''''''''1BP BP 11PC PC 02, PQ AB R CQ AR CQ AR AR AR QA R B QA RB R B RB P Q R ABC R R AB AB R R AB R R AR AR ??=??=?>证:设直线与直线交于,于是由定理得:又,则:=由于在同一直线上的、、三点中,位于边上的点的个数也为或,因此与或者同在线段上,或者同在的延长线上; 若与同在线段上,则与必定重合,不然的话,设'''' '' ,,AR AR AR AR AB AR AB AR BR BR BR BR BR BR -<-<>这时即于是可得这与=矛盾 ''R R AB R R P Q R 类似地可证得当与同在的延长线上时,与也重合 综上可得:、、三点共线; 注:此定理常用于证明三点共线的问题,且常需要多次使用 再相乘; 1111112.P ABC A B C P BC CA AB A B C ?例点位于的外接圆上;、、是从点向、、引的垂线的垂足,证明点、、共线; 111111111 111111 cos , cos cos cos ,cos cos ,,1BA BP PBC CA CP PCB CB AC CP PCA AP PAB AB AP PAC BC PB PBA PAC PBC PAB PCB PCA PBA BA CB AC A B C CA AB BC ?∠=-?∠?∠?∠=-=-?∠?∠∠=∠∠=∠∠+∠=??证:易得:将上面三条式子相乘,且 可得,依梅涅劳斯定理可知、、三点共线; 1111 11111111 1::K A B C D AC A D AC AD A B C D BC BD B C B D =【练习】从点引四条直线,另两条直线分别交这四条直线于、、、和、、、,试证:2ABC BC CA AB D E F EF BC FD CA DE AB X Y Z ?【练习】设不等腰的内切圆在三边、、上的切点分别为、、,则与,与,与的交点、、在同一条直线上; 1111121121122223AA BB CC O AB A B C BC B C A AC A C B A B C 【练习】已知直线,,相交于,直线和的交点为,直线与的交点是,直线与的交点是,试证:、、三点共线; 4E C A B F D AB ED CD AF CD AF EF BC L M N L M N 【练习】在一条直线上取点、、,在另一条上取点、、,记直线和,和,和, 和的交点依次为、、,证明:、、共线 平面几何的几个重要的定理(一) 梅涅劳斯定理 一、基础知识 梅涅劳斯定理 若直线l 不经过△ABC 的顶点,并且与△ABC 的三边BC 、CA 、AB 或它们 的延长线分别交于P 、Q 、R ,则1BP CQ AR PC QA RB ??= 梅涅劳斯定理的逆定理 设P 、Q 、R 分别是△ABC 的三边BC 、CA 、AB 或它们的延长线 上的三点(并且P 、Q 、R 三点中,位于△ABC 边上的点的个数为 0或2),若1BP CQ AR PC QA RB ??=,则P 、Q 、R 三点共线. 由和分比定理可得 R R '∴与重合 ∴P 、Q 、R 三点共线 二、典型例题与基本方法 1. 恰当地选择三角形及其截线(或作出截线),是应用梅涅劳斯定理的关键 例1 如图,在四边形ABCD 中,△ABD 、△BCD 、△ABC 的面积之比是3∶4∶1,点M 、N 分别在AC 、CD 上,满足AM ∶AC =CN ∶CD ,且B 、M 、N 三点共线.求证:M 与N 分别是AC 和CD 的中点. A C D M N 1A B C C B A C A B h h h A B C l h h h BP CQ AR PC QA RB h h h ??=??=证:设、、分别是、、到直线的垂线的长度,则:BP 1PC CQ AR PQ AB R QA R B ''??='证:设直线与直线交于,于是由梅氏定理得:BP 1PC CQ AR AR AR QA RB R B RB '? ?='又,则:=AR AR AB AB '= 2. 梅涅劳斯定理的逆用(逆定理的应用)与迭用,是灵活应用梅氏定理的一种方法 例2 点P 位于△ABC 的外接圆上,111A B C 、、是从点P 向BC 、 CA 、AB 引的垂线的垂足,证明点111A B C 、、共线. 三、解题思维策略分析 1. 寻求线段倍分的一座桥梁 例3 △ABC 是等腰三角形,AB=AC ,M 是BC 的中点;O 是AM 延长线上的一点,使得 OB ⊥AB ; Q 为线段BC 上不同于B 和C 的任意一点,E 、F 分别在直线AB 、AC 上使得E 、Q 、F 是不同的和共线的.求证: (1)若OQ EF ⊥,则QE QF =;(2)若QE QF =,则OQ EF ⊥ . 111111*********|cos |,|cos | |cos ||cos ||cos ||cos |,,1801BA BP PBC CA CP PCB CB CP PCA AB AP PAC AC AP PAB BC PB PBA PAC PBC PAB PCB PCA PBA BA CB AC CA AB BC A B C ?∠=?∠?∠=?∠?∠=?∠∠=∠∠=∠∠+∠=???证:易得:将上面三个式子相乘,且可得=依梅涅劳斯定理可知、、三点共线 . 梅涅劳斯定理 梅涅劳斯(Menelaus)定理(简称梅氏定理)是由古希腊数学家梅涅劳斯首先证明的。它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1 。 展开 定理的证明 证明:当直线交△ABC的AB、BC、CA的反向延长线于点D、E、F时, (AD/DB)*(BE/EC )*(CF/FA)=1 逆定理证明: 证明:X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1 证明一 过点A作AG∥BC交DF的延长线于G, 则AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG 三式相乘得:(AF/FB)×(BD/DC)×(CE/EA)=(AG/BD)×(BD/DC)×(DC/AG)=1 证明二 过点C作CP∥DF交AB于P,则BD/DC=FB/PF,CE/EA=PF/AF 所以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=1 证明三 连结BF。 (AD:DB)·(BE:EC)·(CF:FA) =(S△ADF:S△BDF)·(S△BEF:S△CEF)·(S△BCF:S△BAF) =(S△ADF:S△BDF)·(S△BDF:S△CDF)·(S△CDF:S△ADF) =1 证明四 过三顶点作直线DEF的垂线,AA‘,BB',CC' 有AD:DB=AA’:BB' 另外两个类似,三式相乘得1 得证。如百科名片中图。 充分性证明: △ABC中,BC,CA,AB上的分点分别为D,E,F。 连接DF交CA于E',则由充分性可得,(AF/FB)×(BD/DC)×(CE'/E'A)=1 设0是厶ABC内任意一点, AB、BO、CO 分别交对边于 D、E、F,贝U BD/DC*CE/EA*AF/FB=1 (I)本题可利用梅内劳斯定理证明: ???△ ADC被直线BOE所截, CB/BD*DO/OA*AE/EC=1 ① 而由△ ABD 被直线 COF 所截,??? BC/CD*DO/OA*AF/DF=1 ② ①十②:即得:BD/DC*CE/EA*AF/FB=1 (n)也可以利用面积关系证明 ?/ BD/DC=S △ ABD/S △ ACD=S △ BOD/S △ COD=(S △ ABD-S △ BOD)/(S △ ACD-S △ COD)=S △ AOB/S △ AOC③同理 CE/EA=S △ BOC/ S △ AOB ④ AF/FB=S △ AOC/S △ BOC ⑤ ③X④X⑤得 BD/DC*CE/EA*AF/FB=1 塞瓦定理: 设P、Q、R分别是MBC的BC、CA、AB边上的点,则AP、BQ、CR三线共点 的充要条件是:氐杀詈」 Q C P C A B i 证:先证必要性:设 AP 、BQ 、CR 相交于点M,贝V : 以上三式相乘,得:_BE .空=1 PC QA RB 再证充分性:若 =1,设AP 与BQ 相交于M ,且直线CM 交AB 于 R , PC QA RB 由塞瓦定理有: 拻. BP CQ AR AR AR ‘ 1,于是:因为R 和R 都在线 PC QA R B R B RB 段AB 上,所以R ‘必与R 重合,故 AP 、BQ 、CR 相交于一点点 M ; 例1:证明:三角形的中线交于一点; 证明:记 ABC 的中线秋,BB r CC,,我们只须证明也BA 1 CB 1 =1 1 C 1B AC B 1A 而显然有:AG 二 GB, BA 二 AC ,CB j 二 B 1A 【练习1】证明:三角形的角平 分线交于一点; 【练习2】证明:锐角三角形的 高交于一点; 例2:在锐角 ABC 中,角.C 的平分线交 于AB 于L,从L 作边AC 和BC 的垂线,垂 足分别是M 和N,设AN 和BM 的交点是 P,证明:CP _ AB B 例3设AD 是 ABC 的高,且D 在BC 边上,若P 是AD 上任一点,BP 、CP 分别与AC 、 AB 交于 E 和 F ,贝U EDA = FDA 证:过A 作AD 的垂线,与DE 、DF 的延长线分别 交于M 、N 。欲证? EDA — FDA 可以转化为证明AM AN :AD _BC 故MN //BC ,可得 AME 三 CDE , ANF 三 BDF AM AE AN AF AE CD “ AF BD BD BF CE BF CF 共点于P,根据塞瓦定理可得:-BD C^ =1 BP PC S ACP S'CMP S ACM CQ _ S 'BCM QA AR _ S ACM RB Sp cM 证:作CK _AB 下证CK 、BM 、AN 三线共点,且为 依塞瓦定理 即要证明: 即要证:如空聖=1又丫 MC 二CN MC NB AK BK AM AL 1 + AML = : AKC 二 NB BK BC —:: = NB BL AM AK BNL 三 BKC AK 匹=1 BL 依三角形的角平分线定理可知: .CK 、BM 、AN 三线共点,且为 即要证 AC AL BC AC BL P 点 CP _ AB P 点,要证 CK 、BM 、AN 三线共点, C AC M A K \ # K A CD _CE T AD 、BE 、 BA 1 CB-i C 1B 即 JAC2 AC B 1A 1成立,厶ABC 交于一点; C 梅涅劳斯定理的应用练 习 集团公司文件内部编码:(TTT-UUTT-MMYB-URTTY-ITTLTY- 平面几何问题: 1.梅涅劳斯定理 一直线分别截△ABC 的边BC 、CA 、AB (或其延长线)于D 、E 、 F ,则 1FB AF EA CE DC BD =??。 背景简介:梅涅劳斯(Menelaus )定理是由古希腊数学家梅涅劳斯首先证明的。 证明: 说明: (1)结论的图形应考虑直线与三角形三边交点的位置情况,因而本题图形应该有两个。 (2)结论的结构是三角形三边上的6条线段的比,首尾相连,组成一个比值为1的等式。 (3)梅氏定理及其逆定理不仅可以用来证明点共线问题,而且是解决许多比例线段问题的有力工具。用梅氏定理求某个比值的关键,在于恰当地选取梅氏三角形和梅氏线。 梅涅劳斯定理的逆定理:如果有三点F 、 D 、 E 分别在△ABC 的三边AB 、BC 、CA 或其 延长线上,且满足 1EA CE DC BD FB AF =??,那么F 、D 、E 三点共线。 利用梅涅劳斯定理的逆定理可判定三点共线。 梅涅劳斯定理练习 1.设AD 是△ABC 的边BC 上的中线,直线CF 交AD 于F 。求证: FB AF 2ED AE = 。 2.过△ABC 的重心G 的直线分别交 AB 、AC 于E 、F ,交CB 延长线于 D 。求证: 1FA CF EA BE =+。 3.在△ABC 中,点D 在BC 上, 31 DC BD =,分别在AB ,AD 上,32EB AE =,21 GD AG =,EG 交AC 于点F ,求FC AF 。 4.在□ABCD 中,E ,F 分别是AB ,BC 的中点,AF 与CE 相交于G ,AF 与DE 交于H ,求AH:HG:GF 5.设D 为等腰Rt △ABC (∠C=90°)的直角边BC 的中点,E 在AB 上,且AE :EB=2:1, 梅涅劳斯定理 梅涅劳斯(Menelaus )定理(简称梅氏定理)最早出现在由古希腊数学家梅涅劳斯的著作《球面学》(Sphaerica)。 任何一条直线截三角形的各边,都使得三条不相邻线段之积等于另外三条线段之积,这一定理同样可以轻而易举地用初等几何或通过应用简单的三角关系来证明. 梅涅劳斯把这一定理扩展到了球面三角形。 中文名梅涅劳斯定理 外文名Menelaus 别称梅氏定理 表达式(AF/FB)×(BD/DC)×(CE/EA)=1提出者梅涅劳斯提出时间1678年 应用学科数学,物理适用领域范围平面几何学适用领域范围射影几何学 定理内容 定理证明 证明一 过点A作AG∥DF交BC的延长线于点G.则 证明二 过点C作CP∥DF交AB于P,则 两式相乘得 证明三 连结CF、AD,根据“两个三角形等高时面积之比等于底边之比”的性质有。AF:FB =S △ADF:S△BDF…………(1), BD:DC=S△BDF:S△CDF…………(2), CE:EA=S△CDE:S△ADE=S△FEC:S△FEA =(S△CDE+S△FEC):(S△ADE+S△FEA) =S△CDF:S△ADF (3) (1)×(2)×(3)得 证明四 过三顶点作直线DEF的垂线AA‘,BB',CC',如图: 充分性证明: △ABC中,BC,CA,AB上的分点分别为D,E,F。 连接DF交CA于E',则由充分性可得,(AF/FB)×(BD/DC)×(CE'/E'A)=1 又∵ ∴有CE/EA=CE'/E'A,两点重合。所以共线 推论在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点,又分比是λ=BL/LC、μ=CM/MA、ν=AN/NB。于是AL、BM、CN三线交于一点的充要条件是λμν=-1。(注意与塞瓦定理相区分,那里是λμν=1) 此外,用该定理可使其容易理解和记忆: 第一角元形式的梅涅劳斯定理如图:若E,F,D三点共线,则 (sin∠ACF/sin∠FCB)(sin∠BAD/sin∠DAC)(sin∠CBE/sin∠ABE)=1 即图中的蓝角正弦值之积等于红角正弦值之积。 该形式的梅涅劳斯定理也很实用。 证明:可用面积法推出:第一角元形式的梅氏定理与顶分顶形式的梅氏定理等价。 第二角元形式的梅涅劳斯定理 在平面上任取一点O,且EDF共线,则(sin∠AOF/sin∠FOB)(sin∠BOD/sin∠DOC)(sin ∠COE /sin∠AOE)=1。(O不与点A、B、C重合) 梅涅劳斯球面三角形定理 在球面三角形ABC中,三边弧AB,弧BC,弧CA(都是大圆弧)被另一大圆弧截于P,Q,R 三点,那么 数学意义 使用梅涅劳斯定理可以进行直线形中线段长度比例的计算,其逆定理还可以用来解决三点共线、三线共点等问题的判定方法,是平面几何学以及射影几何学中的一项基本定理,具有重要的作用。梅涅劳斯定理的对偶定理是塞瓦定理。梅涅劳斯定理范文
(完整word版)第1章梅涅劳斯定理及应用
梅涅劳斯定理
梅涅劳斯定理入门篇
数学竞赛 梅涅劳斯定理
梅涅劳斯定理与塞瓦定理
梅涅劳斯定理的应用练习1
梅涅劳斯定理(精选.)
1梅涅劳斯定理及应用
梅涅劳斯定理
梅涅劳斯定理的应用练习1
梅涅劳斯定理及例题拓展
最新高考-梅涅劳斯定理 精品
平面几何的几个重要的定理--梅涅劳斯定理
梅涅劳斯定理及应用
梅涅劳斯定理与塞瓦定理
梅涅劳斯定理的应用练习
数学竞赛 梅涅劳斯定理
