基于matlab的数学实验-线代中的若干问题2

基于MATLAB 的数学实验
——线性代数中的若干问题(二)
2.1 引言
用迭代法(Iteration )寻求问题的答案,是逐步逼近思想的具体体现,其基本思想是:不追求“一下子”得到(非)线性方程(组)的解,而是在逐步逼近方程组的精确解的迭代过程中获得满足精度要求的近似解,这一点与直接法不同;通过对问题的转化,避免(困难的)矩阵求逆运算。在不能或者很难一下子求得结果的情况下,使用迭代法就是一种自然的选择,因此了解并学会使用迭代法是十分有益的。在本节你将了解到 1.什么是迭代;
2.什么样的迭代是可用的;
3.线性迭代、非线性迭代以及二者的差异;
2.2 (非)线性方程的场合
数列是我们熟知的数学概念和对象,下面就是一例
222,
,
, (1)
这个数列产生于这样的过程:从2=x 开始,计算函数()x x f =在x =2点处的值得到数列的第一项,然后将计算结果再代入函数的表达式中得到数列的第二项,数列(1)重复这种操作(迭代)的结果,其中2=x 称为迭代的初值。迭代公式(定义了一种迭代算法)为:n n x x =+1。由此可见,任何函数(包括一元函数和多元函数)在其定义域内都对应一种迭代,线性函数、非线性函数确定的迭代分别称为线性迭代和非线性迭代。面对这无穷多的迭代算法,在实际使用时如何选择呢?下面我们通过一个具体的代数方程求根的例子来说明选择的依据和准则,
例 用迭代法求代数方程根的例子:
让我们来求如下方程的根
()f x x x x x =-++=3223030
.sin . (2)
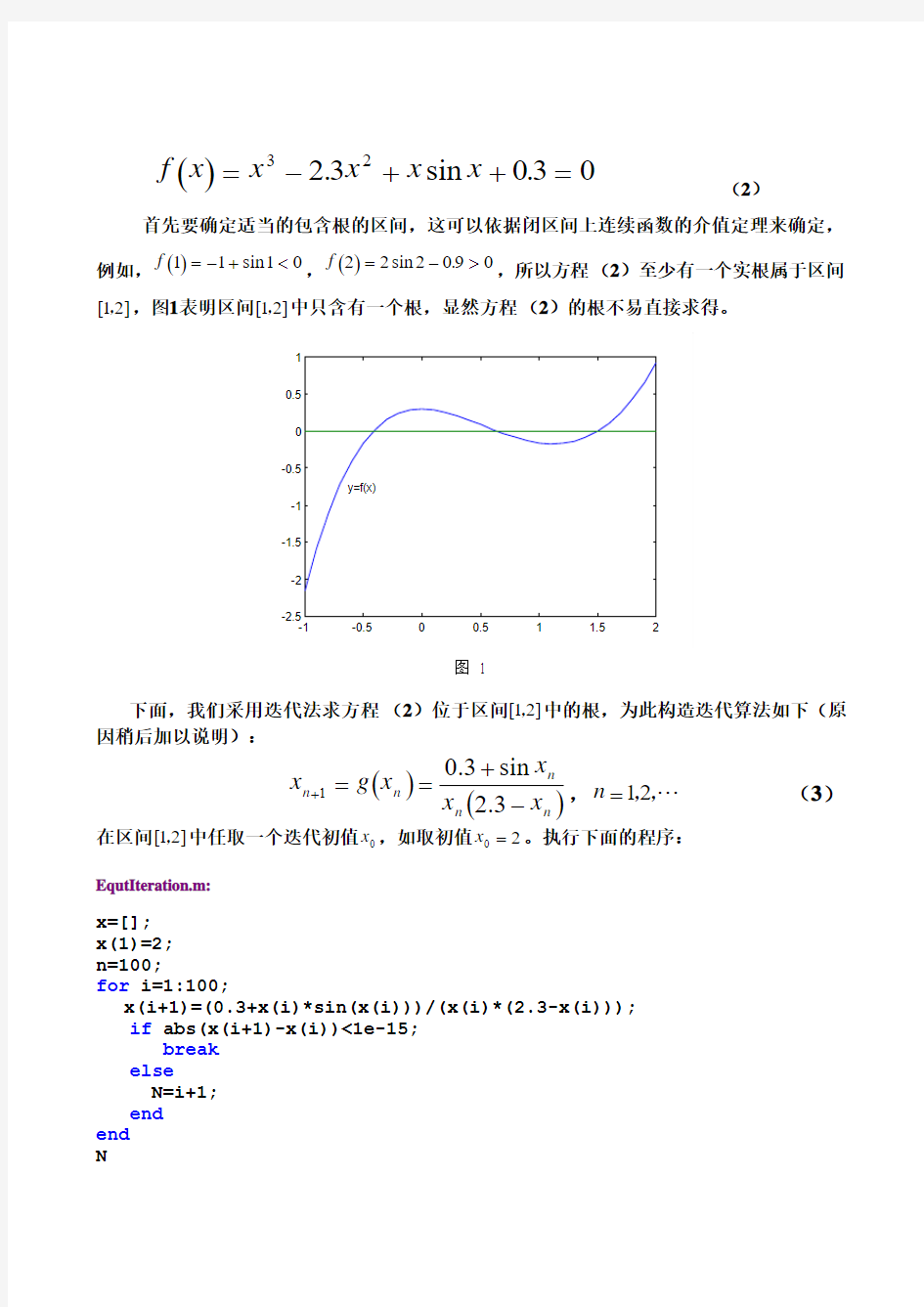
首先要确定适当的包含根的区间,这可以依据闭区间上连续函数的介值定理来确定,
例如,
()f 1110
=-+ ()f 222090 =->sin .,所以方程 (2)至少有一个实根属于区间 ]21[,,图1表明区间]21[,中只含有一个根,显然方程 (2)的根不易直接求得。 图 1 下面,我们采用迭代法求方程 (2)位于区间]21[,中的根,为此构造迭代算法如下(原因稍后加以说明): ()()n n n n n x x x x g x -+==+3.2sin 3.01 , ,, 21=n (3) 在区间]21[,中任取一个迭代初值0x ,如取初值20=x 。执行下面的程序: EqutIteration.m: x=[]; x(1)=2; n=100; for i=1:100; x(i+1)=(0.3+x(i)*sin(x(i)))/(x(i)*(2.3-x(i))); if abs(x(i+1)-x(i))<1e-15; break else N=i+1; end end N x plot([1:length(x)],x) title('ITERATION FOR SOLVING EQUATION') gtext('Curve of Iteration') 共迭代42次,得到结果如下: x n = 2.0000 3.5310 0.2394 0.7233 0.6828 0.6618 0.6519 0.6473 0.6453 0.6444 0.6441 0.6439 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 0.6438 可以看出n=13以后,在取4位有效数字时x n 不再变化,下图也表明了这一事实,事实上(能够证明)用迭代所求方程的根,误差不超过9.91514e-020 ,这是相当精确的。 051015202530354045 ITERATION FOR SOLVING EQUATION 图 2 以上我们已经看到,按迭代算法(3 定理 设方程()0=x f 在][b a ,上存在唯一解,()x g x =1、()x g 在][b a ,上连续可微; 2、对任何][b a x ,∈,()][b a x g ,∈; 3、()1<≤'L x g , 则对任何][0b a x ,∈,由迭代算法 () x g x n n +=1, (4) 生成的序列{}n x 收敛于方程()0=x f 在][b a ,上的唯一解。 问题与实验1:用迭代算法(3)能否求出方程(2)的所有解?不妨用程序EqutIteration.m 先做实验,再说明原因。 问题与实验2:就方程(2)或选择别的例子构造不同的收敛迭代法,通过实验和比较,你可能会有所感悟。 2.3 (非)线性方程组的场合 用迭代法求解线性方程组,首先要把线性方程组写成等价的形式 f Mx x b Ax +=?= (5) 式(5)的右端称为迭代格式,由迭代格式(5)确定如下的迭代算法: ,2,10 1=???∈?+=+m R x f Mx x n m m (6) 对于给定的线性方程组,可以写成不同的(无穷多)迭代格式,有意义的(可用的)迭代格式应具有收敛性―生成的解向量序列{} x n 收敛于方程组的解;而好的迭代法应具有较高的收敛速度。 关于迭代法收敛性的两个判别条件: a 、充分必要条件是:矩阵M 的谱半径 (){}1,,2,1max <==n i M i i λρ b 、充分条件是:矩阵M 的某个算子范数M <1。 设x 是方程组(5)的解,{}m x 是迭代法(6)生成的任一序列,因为 f Mx x +=,f Mx x m m +=+1 所以 ()()()0221x x M x x M x x M x x m m m m -==-=-=--- (7) 设1 1--=?=TJT M J MT T ,其中矩阵J 是矩阵M 的Jordan 标准型,那么容易验证 1-=T TJ M m m ,并且 ()[] () ()()1 0lim ,2,10 lim lim 0 lim lim 010 →+∞ →-+∞ →+∞ →+∞ →M M n i x x T J T x x M x x m m m i n m m m m m m ρρλ (8) 此外,因为 ()0 22 11x x M x x M x x M x x M x x m m m m m -≤≤-≤-≤-=---- (9) 所以 x x x x M M m m m m m m =?=-?=?<+∞ →+∞ →+∞ →lim 0lim 0lim 1 (10) 注:迭代格式(6)所确定的迭代法收敛与否,完全由系数矩阵M 决定,而与常数项f 无关. 例 用迭代法求线性方程组根的例子: 让我们来求5阶线性方程组: 其中 A= [4.3999 0.6686 -1.6041 0.5287 -1.0106; 0.6900 5.1908 0.2573 0.2193 0.6145; 0.8156 -1.2025 4.0565 -0.9219 0.5077; 0.7119 -0.0198 1.4151 3.1707 1.6924; 1.2902 -0.1567 -0.8051 -0.0592 5.5913] b=[ -0.4326; -1.6656;0.1253;0.2877;-1.1465] 构造迭代法(Jacobi 迭代法)如下: x Mx f n n +=+1 (5) 其中{}D diad a a a =112255,,, , []M D D A =--1= [0 -0.1520 0.3646 -0.1202 0.2297 -0.1329 0 -0.0496 -0.0422 -0.1184 -0.2011 0.2964 0 0.2273 -0.1252 -0.2245 0.0062 -0.4463 0 -0.5338 -0.2308 0.0280 0.1440 0.0106 0] f D b =-1 =[ -0.0983 -0.3209 0.0309 0.0907 -0.2051] 使用程序 ITERA_J : A= [4.3999 0.6686 -1.6041 0.5287 -1.0106; 0.6900 5.1908 0.2573 0.2193 0.6145; 0.8156 -1.2025 4.0565 -0.9219 0.5077; 0.7120 -0.0198 1.4151 3.1707 1.6924; 1.2902 -0.1567 -0.8051 -0.0592 5.5913]; b=[ -0.4326; -1.6656;0.1253;0.2877;-1.1465] D=diag(diag(A)); LU=D-A; M=D\LU; f=D\b; x=[]; z=[]; x(:,1)=eye(5,1); N=2000; for i=1:N; if norm(A*x(:,i)-b)<1e-010; m=i; break else x(:,i+1)=M*x(:,i)+f; z=x(:,i+1); end end m e=norm(A*z-b) plot([1:length(x)],x) title('JACOBI ITERATION OF LINEAR EQUATIONS') gtext('x1') gtext('x2') gtext('x3') gtext('x4') gtext('x5') 迭代42次,误差向量e Ax b =-42<7.0162e-011,并且看出n =23以后,在取4位有效数字时x n 不再变化,迭代过程如图3所示。 图3 问题与实验3: 一元线性迭代的收敛性条件怎样表述? 问题与实验4: 在本例中,12 12 和12 ≥M 构造不同的迭代法,通过实验和比较,并给出你对实验结果的解释(如 关于收敛性、收敛速度等),当然这需要你首先知道矩阵范数的概念,并且对它有比较好的理解。 1.4 不动点、k 循环与混沌 我们已经知道任何函数(包括一元函数和多元函数)在其定义域内都对应一种迭代,对于非线性函数迭代来说,不动点是下面所定义的k —循环的特例(1—循环): 定义: 设由迭代算法()n n x g x =+1, ,,10=n ,生成的序列{}n x 具有如下性质:N k ∈?(自然数集合),∈?0x ][b a ,,()000>?x N ,当()00x N n ≥时, k n n x x +=,i n n x x +≠,k i < (6) 那么称k n n n x x x ++,, , 1是由迭代算法()n n x g x =+1生成的k —循环。 引例 关于迭代 () x a x a n n +=--12 (7) 实验与讨论。 容易求得迭代(7)有两个不动点:0*=x 和12*-=a x ,图4给出了a =2及迭代初值 分别取0100. =x 和900.=x 时,迭代收敛于12*-=a x 的情形: 使用程序(ITERA1:) a=2; x=[];y=[]; x(1)=input('please input the firse value of iteration x(1)=:');%x(1)=0.01 y(1)=input('please input the firse value of iteration y(1)=:');%y(1)=0.9 n=input('please input the total number of iteration n=:');%n=150 for i=1:n-1; x(i+1)=a-(x(i)-sqrt(a))^2; y(i+1)=a-(y(i)-sqrt(a))^2; end subplot(2,1,1) plot(1:n,x,'bo') title('ITERATION FOR SOLVING EQUATION') subplot(2,1,2) plot(1:n,y,'r*') title('ITERATION FOR SOLVING EQUATION') ITERATION FOR SOLVING EQUATION 050100150 ITERATION FOR SOLVING EQUATION 图 4 图5给出了a =3时,出现4—循环的情形: 使用程序(ITERA2:) a=3; x=[]; x(1)=input('please input the firse value of iteration x(1)=:');%2.5 n=input('please input the total number of iteration n=:');%n=200 for i=1:n-1; x(i+1)=a-(x(i)-sqrt(a))^2; end plot(1:n,x,'r*') title('ITERATION FOR SOLVING EQUATION') ITERATION FOR SOLVING EQUATION 图 5 图6给出了16.3=a 时,出现8—循环的情形: 使用程序(ITERA3:) a=3.16; x=[]; x(1)=input('please input the firse value of iteration x(1)=:');%1.5 n=input('please input the total number of iteration n=:');%n=500 for i=1:n-1; x(i+1)=a-(x(i)-sqrt(a))^2; end plot(1:n,x,'r*') title('ITERATION FOR SOLVING EQUATION') 50 100 150 200 250 300 350 400 450 500 ITERATION FOR SOLVING EQUATION 图 6 图7给出了a =4时,出现混沌现象的情形,迭代初值分别取0100. =x 、4999900.=x 、5000100.=x 和900. =x 。 使用程序(ITERA4:) a=4; x=[];y=[]; x(1)=input('please input the firse value of iteration x(1)=:');%x(1)=0.50001 y(1)=input('please input the firse value of iteration y(1)=:');%y(1)=0.9 n=input('please input the total number of iteration n=:');%n=150 for i=1:n-1; x(i+1)=a-(x(i)-sqrt(a))^2; y(i+1)=a-(y(i)-sqrt(a))^2; end subplot(2,1,1) plot(1:n,x,'bo') title('ITERATION FOR SOLVING EQUATION') subplot(2,1,2) plot(1:n,y,'r*') title('ITERATION FOR SOLVING EQUATION') 图 7 图 8 下面的两组图形则是在同一组迭代初值的情况下,a分别等于3.70和3.75时的迭代情形: 使用程序(ITERA5:) a=3.70; x=[];y=[]; x(1)=input('please input the firse value of iteration x(1)=:');%x(1)=0.001 y(1)=input('please input the firse value of iteration y(1)=:');%y(1)=0.9 n=input('please input the total number of iteration n=:');%n=300 for i=1:n-1; x(i+1)=a-(x(i)-sqrt(a))^2; y(i+1)=a-(y(i)-sqrt(a))^2; end subplot(2,1,1) plot(1:n,x,'bo') title('ITERATION FOR SOLVING EQUATION') subplot(2,1,2) plot(1:n,y,'r*') title('ITERATION FOR SOLVING EQUATION') ITERATION FOR SOLVING EQUATION ITERATION FOR SOLVING EQUATION . 图 9 a 37 ITERATION FOR SOLVING EQUATION ITERATION FOR SOLVING EQUATION 图 10 a =375. 问题与实验5:对迭代()2 1a x a x n n --=+,通过进一步的实验和观察寻找更多的k —循环的情况,并借助于必要的理论分析,讨论次迭代出现k —循环的原因。 问题与实验6:对迭代( ) 2 1a x a x n n --=+,通过进一步的实验和观察确定可以出现混沌的参数a 的取值范围,混沌现象的出现是否与迭代初值有关? 问题与实验7:通过对迭代a x x n n -=+2 1和(或)n n x a x sin 1=+的实验和观察,进一步认识迭代的k —循环和混沌现象。 数学软件与数学实验作业 一.《数学软件》练习题(任选12题,其中19-24题至少选2题): 3.对下列各式进行因式分解. (1). syms x y >> factor(x^5-x^3) (2). syms x y >> factor(x^4-y^4) (3). syms x >> factor(16-x^4) (4). syms x >> factor(x^3-6*x^2+11*x-6) (5). syms x y >> factor((x+y)^2-10*(x+y)+25) (6). syms x y >> factor(x^2/4+x*y+y^2) (7). syms x y a b >> factor(3*a*x+4*b*y+4*a*y+3*b*x) (8). syms x >> factor(x^4+4*x^3-19*x^2-46*x+120) 5.解下列方程或方程组. (1).solve('(y-3)^2-(y+3)^3=9*y*(1-2*y)') (2). solve('3*x^2+5*(2*x+1)') (3). solve('a*b*x^2+(a^4+b^4)*x+a^3*b^3','x') (4). solve('x^2-(2*m+1)*x+m^2+m','x') (5). [x,y]=solve('4*x^2-9*y^2=15','2*x-3*y=15') 6.计算极限. (1). syms x f=(exp(x)-exp(-x))/sin(x); limit(f,x,0) (2) syms x >> f=(x/(x-1)-1/log(x)); >> limit(f,x,1) (3). syms x >> f=(1-cos(x))/x^2; >> limit(f,x,0) 数学软件课程设计 题目非线性方程求解 班级数学081 姓名曹曼伦 实验目的:用二分法与Newton迭代法求解非线性方程的根; 用Matlab函数solve、fzero、fsolve求解非线性方程(组)的解。 编程实现二分法及Newton迭代法; 学会使用Matlab函数solve、fzero、fsolve求解非线性方程(组)的解。 通过实例分别用二分法及迭代法解非线性方程组并观察收敛速度。 实验内容: 比较求exp(x)+10*x-2的根的计算量。(要求误差不超过十的五次方) (1)在区间(0,1)内用二分法; (2)用迭代法x=(2-exp(x))/10,取初值x=0 。 试验程序 (1)二分法: format long syms x s=exp(x)+10*x-2 a=0; b=1; A=subs(s,a) B=subs(s,b) f=A*B %若f<0,则为由根区间 n=0; stop=1.0e-5; while f<0&abs(a-b)>=stop&n<=100; Xk=(a+b)/2; %二分 M= subs(s, Xk); if M* A<0 symbol=1 %若M= subs(s, Xk)为正,则与a二分 b= Xk else symbol=0 % 若M= subs(s, Xk)为负,则与b二分 a= Xk end n=n+1 end Xk n (2)牛顿迭代法; format long syms x s= (2-exp(x))/10; %迭代公式 f=diff(s); x=0; %迭代初值 a=subs(f,x); %判断收敛性(a是否小于1) s=(2-exp(x))/10; stop=1.0e-5; %迭代的精度 n=0; while a<1&abs(s-x)>=stop&n<=100; x=s %迭代 s=(2-exp(x))/10; n=n+1 end 实验结果: (1)二分法: symbol =1 b =0.50000000000000 n =1 symbol =1 b =0.25000000000000 n =2 symbol =1 b =0.12500000000000 n =3 symbol =0 a =0.06250000000000 n =4 symbol =1 b =0.09375000000000 n =5 symbol =0 a =0.07812500000000 n =6 symbol =1 b =0.09054565429688 n =15 symbol =1 b =0.09053039550781 n =16 symbol =0 a =0.09052276611328 n =17 Xk =0.09052276611328 n =17 (2)迭代法 由x =0.10000000000000 n =1 x =0.08948290819244 n =2 x =0.09063913585958 n =3 x =0.09051261667437 n =4 x =0.09052646805264 n =5 试验结果可见用二分法需要算17次,而用迭代法求得同样精度的解仅用5次,但由于迭代法一般只具有局部收敛性,因此通常不用二分法来求得非线性方程的精确解,而只用它求得根的一个近似解,再用收敛速度较快的迭代法求得其精确解。 “”练习题 要求:抄题、写出操作命令、运行结果,并根据要求,贴上运行图。 1、求230x e x -=的所有根。(先画图后求解)(要求贴图) >> ('(x)-3*x^2',0) = -2*(-1/6*3^(1/2)) -2*(-11/6*3^(1/2)) -2*(1/6*3^(1/2)) 3、求解下列各题: 1)30 sin lim x x x x ->- >> x; >> (((x))^3) = 1/6 2) (10)cos ,x y e x y =求 >> x; >> ((x)*(x),10) = (-32)*(x)*(x) 3)2 1/2 0(17x e dx ?精确到位有效数字) >> x; >> ((((x^2),0,1/2)),17) = 0.54498710418362222 4)4 2 254x dx x +? >> x; >> (x^4/(25^2)) = 125*(5) - 25*x + x^3/3 5)求由参数方程arctan x y t ??=? =??dy dx 与二阶导 数22 d y dx 。 >> t; >> ((1^2))(t); >> ()() = 1 6)设函数(x)由方程e所确定,求y′(x)。>> x y; *(y)(1); >> ()() = (x + (y)) 7) sin2 x e xdx +∞- ? >> x; >> ()*(2*x); >> (y,0) = 2/5 8) 08x =展开(最高次幂为) >> x (1); taylor(f,0,9) = - (429*x^8)/32768 + (33*x^7)/2048 - (21*x^6)/1024 + (7*x^5)/256 - (5*x^4)/128 + x^3/16 - x^2/8 + 2 + 1 9) 1sin (3)(2)x y e y =求 >> x y; >> ((1)); >> ((y,3),2) = 数学实验答案 Chapter 1 Page20,ex1 (5) 等于[exp(1),exp(2);exp(3),exp(4)] (7) 3=1*3, 8=2*4 (8) a为各列最小值,b为最小值所在的行号 (10) 1>=4,false, 2>=3,false, 3>=2, ture, 4>=1,ture (11) 答案表明:编址第2元素满足不等式(30>=20)和编址第4元素满足不等式(40>=10) (12) 答案表明:编址第2行第1列元素满足不等式(30>=20)和编址第2行第2列元素满足不等式(40>=10) Page20, ex2 (1)a, b, c的值尽管都是1,但数据类型分别为数值,字符,逻辑,注意a与c相等,但他们不等于b (2)double(fun)输出的分别是字符a,b,s,(,x,)的ASCII码 Page20,ex3 >> r=2;p=0.5;n=12; >> T=log(r)/n/log(1+0.01*p) Page20,ex4 >> x=-2:0.05:2;f=x.^4-2.^x; >> [fmin,min_index]=min(f) 最小值最小值点编址 >> x(min_index) ans = 0.6500 最小值点 >> [f1,x1_index]=min(abs(f)) 求近似根--绝对值最小的点 f1 = 0.0328 x1_index = 24 >> x(x1_index) ans = -0.8500 >> x(x1_index)=[];f=x.^4-2.^x; 删去绝对值最小的点以求函数绝对值次小的点 >> [f2,x2_index]=min(abs(f)) 求另一近似根--函数绝对值次小的点 f2 = 0.0630 x2_index = 65 >> x(x2_index) ans = 1.2500 Matlab 数学实验 实验一 插值与拟合 实验内容: 预备知识:编制计算拉格朗日插值的M 文件。 1. 选择一些函数,在n 个节点上(n 不要太大,如5 ~ 11)用拉格朗日、分段线性、三次样条三种插值方法,计算m 个插值点的函数值(m 要适中,如50~100)。通过数值和图形输出,将三种插值结果与精确值进行比较。适当增加n ,再做比较,由此作初步分析。下列函数任选一种。 (1)、 ;20,sin π≤≤=x x y (2)、;11,)1(2/12≤≤--=x x y (3)、;22,c o s 10 ≤≤-=x x y (4)、22),exp(2≤≤--=x x y 2.用电压V=10伏的电池给电容器充电,电容器上t 时刻的电压为 ) (0)()(t e V V V t v ---=,其中0V 是电容器的初始电压,τ是充电常数。试由下面 一组t ,V 数据确定0V 和τ。 实验二 常微分方程数值解试验 实验目的: 1. 用MATLAB 软件求解微分方程,掌握Euler 方法和龙格-库塔方法; 2. 掌握用微分方程模型解决简化的实际问题。 实验内容: 实验三地图问题 1.下图是一个国家的地图,为了计算出它的国土面积,首先对地图作如下测量: 以由西向东方向为x轴,由南到北方向为y轴,选择方便的原点,并将从最西边界点到最东边界点在x轴上的区间适当地划分为若干段,在每个分点的y方向测出南边界点和北边界点的y坐标y1和y2,这样就得到了表中的数据(单位mm)。 根据地图的比例我们知道18mm相当于40km,试由测量数据计算该国土 的近似面积,并与它的精确值41288km2比较。 数学实验 期 末 作 业 学号: 班级: 姓名: 1. 求函数x x y 2sin 3=的5阶导数。 2. 使用sparse 命令描述? ? ???? ? ? ??30001 020******* 01020 10003。 3. 求解边值问题 1)0(,0)0(,34,43==+-=+=g f g f dx dg g f dx df 。 4. 建立函数1 2sin )(3-=x x f x 的M-文件,并计算)2(f 和)10(f 。 5. 计算二重积分dy dx x y ??211 0][。 6. 已知数列满足2,11 01=+= +a ka a k k ,求5a ,并要求最后结果分别以小数点后两位和有理数这两种数据显示格式输出。 7. 大约在1500年前,《孙子算经》中就记载了这个有趣的问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”请根据你的思路编程求解。 8. 绘制以下方程所表示的图形。 (1)x x y -=23 2 (2)y z cos =绕z 轴的旋转曲面 (3))40(,) 2sin(sin )]2cos(4[cos )]2cos(4[π< 10.根据中华人民共和国个人所得税法规定:公民的个人工资、薪金应依法缴纳个人所得税。所得税计算办法为:在每个人的月收入中超过2000元以上的部分应该纳税,这部分收入称为应纳税所得额。应纳税所得额实行分段累计税率,按下列税率表计算: 个人所得税税率表: 等级全月应纳税所得额税率(%) 1 不超过500元的部分 5 2 超过500元,不到2000元的部分10 3 超过2000元,不到5000元的部分15 4 超过5000元,不到20000元的部分20 5 超过20000元,不到40000元的部分25 6 超过40000元,不到60000元的部分30 7 超过60000元,不到80000元的部分35 8 超过80000元,不到100000元的部分40 9 超过100000元的部分45 若某人的工资是x元,试建立税款y与收入x之间的M-文件,并要求程序运行时可以告知操作者“please input the number of your wage”。 实验一 MATLAB 环境的熟悉与基本运算 一、实验目的及要求 1.熟悉MATLAB 的开发环境; 2.掌握MATLAB 的一些常用命令; 3.掌握矩阵、变量、表达式的输入方法及各种基本运算。 二、实验内容 1.熟悉MATLAB 的开发环境: ① MATLAB 的各种窗口: 命令窗口、命令历史窗口、工作空间窗口、当前路径窗口。 ②路径的设置: 建立自己的文件夹,加入到MATLAB 路径中,并保存。 设置当前路径,以方便文件管理。 2.学习使用clc 、clear ,了解其功能和作用。 3.矩阵运算: 已知:A=[1 2;3 4]; B=[5 5;7 8]; 求:A*B 、A.*B ,并比较结果。 4.使用冒号选出指定元素: 已知:A=[1 2 3;4 5 6;7 8 9]; 求:A 中第3列前2个元素;A 中所有列第2,3行的元素; 5.在MATLAB 的命令窗口计算: 1) )2sin(π 2) 5.4)4.05589(÷?+ 6.关系及逻辑运算 1)已知:a=[5:1:15]; b=[1 2 8 8 7 10 12 11 13 14 15],求: y=a==b ,并分析结果 2)已知:X=[0 1;1 0]; Y=[0 0;1 0],求: x&y+x>y ,并分析结果 7.文件操作 1)将0到1000的所有整数,写入到D 盘下的文件 2)读入D 盘下的文件,并赋给变量num 8.符号运算 1)对表达式f=x 3 -1 进行因式分解 2)对表达式f=(2x 2*(x+3)-10)*t ,分别将自变量x 和t 的同类项合并 3)求 3(1)x dz z +? 三、实验报告要求 完成实验内容的3、4、5、6、7、8,写出相应的程序、结果 数学实验报告 制作成员班级学号 2011年6月12日 培养容器温度变化率模型 一、实验目的 利用matlab软件估测培养容器温度变化率 二、实验问题 现在大棚技术越来越好,能够将温度控制在一定温度范围内。为利用这种优势,实验室现在需要培植某种适于在8.16℃到10.74℃下能够快速长大的甜菜品种。为达到实验所需温度,又尽可能地节约成本,研究所决定使用如下方式控制培养容器的温度:1,每天加热一次或两次,每次约两小时; 2,当温度降至8.16℃时,加热装置开始工作;当温度达到10.74℃时,加热装置停止工作。 已知实验的时间是冬天,实验室为了其它实验的需要已经将实验室的温度大致稳定在0℃。下表记录的是该培养容器某一天的温度 时间(h)温度(℃)时间(h)温度(℃)09.68 1.849.31 0.929.45 2.959.13 3.878.981 4.989.65 4.988.811 5.909.41 5.908.691 6.839.18 7.008.5217.938.92 7.938.3919.048.66 8.978.2219.968.43 9.89加热装置工作20.848.22 10.93加热装置工作22.02加热装置工作10.9510.8222.96加热装置工作12.0310.5023.8810.59 12.9510.2124.9910.35 13.889.9425.9110.18 三、建立数学模型 1,分析:由物理学中的傅利叶传热定律知温度变化率只取决于温度 差,与温度本身无关。因为培养容器最低温度和最高温度分别是:8.16℃和10.74℃;即最低温度差和最高温度差分别是:8.16℃和10.74℃。而且,16.8/74.10≈1.1467,约为1,故可以忽略温度对温度变化率的影响2, 将温度变化率看成是时间的连续函数,为计算简单,不妨将温度变化率定义成单位时间温度变化的多少,即温度对时间连续变化的绝对值(温度是下降的),得到结果后再乘以一系数即可。 四、问题求解和程序设计流程1)温度变化率的估计方法 根据上表的数据,利用matlab 做出温度-时间散点图如下: 下面计算温度变化率与时间的关系。由图选择将数据分三段,然后对每一段数据做如下处理:设某段数据为{(0x ,0y ),(1x ,1y ),(2x , 2y ),…,(n x ,n y )},相邻数据中点的平均温度变化率采取公式: 温度变化率=(左端点的温度-右端点的温度)/区间长度算得即:v( 2 1i i x x ++)=(1+-i i y y )/(i i x x - +1). 每段首尾点的温度变化率采用下面的公式计算:v(0x )=(30y -41y +2y )/(2x -0x )v(n x )=(3n y -41+n y +2+n y )/(n x -2-n x ) 一元函数微分学 实验1 一元函数的图形(基础实验) 实验目的 通过图形加深对函数及其性质的认识与理解, 掌握运用函数的图形来观察和分析 函数的有关特性与变化趋势的方法,建立数形结合的思想; 掌握用Matlab 作平面曲线图性的方法与技巧. 初等函数的图形 2 作出函数x y tan =和x y cot =的图形观察其周期性和变化趋势. 解:程序代码: >> x=linspace(0,2*pi,600); t=sin(x)./(cos(x)+eps); plot(x,t);title('tan(x)');axis ([0,2*pi,-50,50]); 图象: 程序代码: >> x=linspace(0,2*pi,100); ct=cos(x)./(sin(x)+eps); plot(x,ct);title('cot(x)');axis ([0,2*pi,-50,50]); 图象: cot(x) 4在区间]1,1[-画出函数x y 1 sin =的图形. 解:程序代码: >> x=linspace(-1,1,10000); y=sin(1./x); plot(x,y); axis([-1,1,-2,2]) 图象: 二维参数方程作图 6画出参数方程???==t t t y t t t x 3cos sin )(5cos cos )(的图形: 解:程序代码: >> t=linspace(0,2*pi,100); plot(cos(t).*cos(5*t),sin(t).*cos(3*t)); 图象: 极坐标方程作图 8 作出极坐标方程为10/t e r =的对数螺线的图形. 解:程序代码: >> t=0:0.01:2*pi; r=exp(t/10); polar(log(t+eps),log(r+eps)); 图象: 90270 分段函数作图 10 作出符号函数x y sgn =的图形. 解: 数学实验报告 姓名: 班级: 学号: 第一次实验任务 过程: a=1+3i; b=2-i; 结果: a+b =3.0000 + 2.0000i a-b =-1.0000 + 4.0000i a*b = 5.0000 + 5.0000i a/b = -0.2000 + 1.4000i 过程: x=-4.5*pi/180; y=7.6*pi/180; 结果: sin(abs(x)+y)/sqrt(cos(abs(x+y))) =0.2098 心得:对于matlab 中的角度计算应转为弧度。 (1)过程: x=0:0.01:2*pi; y1=sin(x); y2=cos(x); y3=exp(x); y4=log(x); plot(x,y1,x,y2,x,y3,x,y4) plot(x,y1,x,y2,x,y3,x,y4) 结果: (2)过程:>> subplot(2,2,1) >> plot(x,y1) >> subplot(2,2,2) >> plot(x,y2) ./,,,,2,311b a b a b a b a i b i a ?-+-=+=计算、设有两个复数 6,7,5.4) cos()sin(2=-=++y x y x y x ,其中、计算的图形。 下分别绘制)同一页面四个坐标系)同一坐标系下(、在( x y e y x y x y x ln ,,cos ,sin 213==== >> subplot(2,2,3) >> plot(x,y3) >> subplot(2.2.4) >> subplot(2,2,4) >> plot(x,y4) 结果: 心得:在matlab中,用subplot能够实现在同一页面输出多个坐标系的图像,应注意将它与hold on进行区别,后者为在同一坐标系中划出多条曲线。 5、随机生成一个3x3矩阵A及3x2矩阵B,计算(1)AB,(2)对B中每个元素平方后得到的矩阵C,(3)sinB,(4)A的行列式,(5)判断A是否可逆,若可逆,计算A的逆矩阵,(6)解矩阵方程AX=B,(7)矩阵A中第二行元素加1,其余元素不变,得到矩阵D,计算D。 过程:A=fix(rand(3,3).*10) ; B=fix(rand(3,3).*10); 《数学实验与MATLAB》 ——综合实验报告 实验名称:不同温度下PDLC薄膜的通透性 与驱动电压的具体关系式的研究学院:计算机与通信工程学院 专业班级: 姓名: 学号: 同组同学: 2014年 6月10日 一、问题引入 聚合物分散液晶(PDLC)是将低分子液晶与预聚物Kuer UV65胶相混合,在一定条件下经聚合反应,形成微米级的液晶微滴均匀地分散在高分子网络中,再利用液晶分子的介电各向异性获得具有电光响应特性的材料,它主要工作在散射态和透明态之间并具有一定的灰度。聚合物分散液晶膜是将液晶和聚合物结合得到的一种综合性能优异的膜材料。该膜材料能够通过驱动电压来控制其通透性,可以用来制作PDLC型液晶显示器等,具有较大的应用范围。已知PDLC薄膜在相同光强度及驱动电压下,不用的温度对应于不同的通透性,不同温度下的阀值电压也不相同。为了尽量得到不同通透性的PDLC薄膜,有必要进行温度对PDLC薄膜的特性的影响的研究。现有不同温度下PDLC 薄膜透过率与驱动电压的一系列数据,试得出不同温度下PDLC薄膜通透性与驱动电压的具体关系式,使得可以迅速得出在不同温度下一定通透性对应的驱动电压。 二、问题分析 想要得到不同温度下PDLC薄膜通透性与驱动电压的具体关系式可以运用MATLAB多项式农合找出最佳函数式,而运用MATLAB多项式插值可以得出在不同温度下一定通透性所对应的驱动电压。 三、实验数据 选择10、20、30摄氏度三个不同温度,其他条件一致。 (1)、10摄氏度 实验程序: x=2:2:40; y=[5.2,5.4,5.8,6.4,7.2,8.2,9.4,10.8,12.2,14.0,16.6,22.0, 30.4,39.8,51.3,55.0,57.5,58.8,59.6,60.2]; p3=polyfit(x,y,3); p5=polyfit(x,y,5); p7=polyfit(x,y,7); disp('三次拟合函数'),f3=poly2str(p3,'x') disp('五次拟合函数'),f5=poly2str(p5,'x') disp('七次拟合函数'),f7=poly2str(p7,'x') x1=0:1:40; y3=polyval(p3,x1); y5=polyval(p5,x1); y7=polyval(p7,x1); plot(x,y,'rp',x1,y3,'--',x1,y5,'k-.',x1,y7); legend('拟合点','三次拟合','五次拟合','七次拟合') 实验结果: 第一次练习 教学要求:熟练掌握Matlab 软件的基本命令和操作,会作二维、三维几何图形,能够用Matlab 软件解决微积分、线性代数与解析几何中的计算问题。 补充命令 vpa(x,n) 显示x 的n 位有效数字,教材102页 fplot(‘f(x)’,[a,b]) 函数作图命令,画出f(x)在区间[a,b]上的图形 在下面的题目中m 为你的学号的后3位(1-9班)或4位(10班以上) 1.1 计算30sin lim x mx mx x →-与3 sin lim x mx mx x →∞- syms x limit((902*x-sin(902*x))/x^3) ans = 366935404/3 limit((902*x-sin(902*x))/x^3,inf) ans = 0 1.2 cos 1000 x mx y e =,求''y syms x diff(exp(x)*cos(902*x/1000),2) ans = (46599*cos((451*x)/500)*exp(x))/250000 - (451*sin((451*x)/500)*exp(x))/250 1.3 计算 22 11 00 x y e dxdy +?? dblquad(@(x,y) exp(x.^2+y.^2),0,1,0,1) ans = 2.1394 1.4 计算4 2 2 4x dx m x +? syms x int(x^4/(902^2+4*x^2)) ans = (91733851*atan(x/451))/4 - (203401*x)/4 + x^3/12 1.5 (10)cos ,x y e mx y =求 syms x diff(exp(x)*cos(902*x),10) ans = -356485076957717053044344387763*cos(902*x)*exp(x)-3952323024277642494822005884*sin(902*x)*exp(x) 1.6 0x =的泰勒展式(最高次幂为4). Matlab实验报告 ——定积分的近似计算 学生姓名: 学号: 专业:数学与应用数学专业 数学实验报告 实验序号:1001114030 日期:2012年10月20日 班级应一姓名陈璐学号1001114030 实验名称:定积分的近似运算 问题背景描述: 利用牛顿—莱布尼茨公式虽然可以精确地计算定积分的值,但它仅适合于被积分函数的原函数能用初等函数表达出来的情形。如果这点办不到或不容易办到, 这就有必要考虑近似计算的方法。在定积分的很多应用问题中,被积函数甚至没 有解析表达式,可能只是一条实验记录曲线,或者是一组离散的采样值,这时只 能应用近似方法去计算相应的定积分。 实验目的: 本实验将主要研究定积分的三种近似计算算法:矩形法、梯形法、抛物线发。对于定积分的近似数值计算,Matlab有专门函数可用。 实验原理与数学模型: 1.sum(a):求数组a的和。 2.format long:长格式,即屏幕显示15位有效数字。 3.double():若输入的是字符则转化为相应的ASCII码;若输入的是整型数之则转化为 相应的实型数值。 4.quad():抛物线法求数值积分。格式:quad(fun,a,b)。此处的fun是函数,并且 为数值形式,所以使用*、/、^等运算时要在其前加上小数点。 5.trapz():梯形法求数值积分。格式:trapz(x,y)。其中x为带有步长的积分区间;y为数 值形式的运算。 6.fprintf(文件地址,格式,写入的变量):把数据写入指定文件。 7.syms 变量1变量2……:定义变量为符号。 8.sym('表达式'):将表达式定义为符号。 9.int(f,v,a,b):求f关于v积分,积分区间由a到b。 10.subs(f,'x',a):将a的值赋给符号表达式f中的x,并计算出值。若简单地使用subs (f),则将f的所有符号变量用可能的数值代入,并计算出值。 实验所用软件及版本:Matlab 7.0.1 Matlab 数学实验报告 一、实验目的 通过以下四组实验,熟悉MATLAB的编程技巧,学会运用MATLAB的一些主要功能、命令,通过建立数学模型解决理论或实际问题。了解诸如分岔、混沌等概念、学会建立Malthu模型和Logistic 模型、懂得最小二乘法、线性规划等基本思想。 二、实验内容 2.1实验题目一 2.1.1实验问题 Feigenbaum曾对超越函数y=λsin(πx)(λ为非负实数)进行了分岔与混沌的研究,试进行迭代格式x k+1=λsin(πx k),做出相应的Feigenbaum图 2.1.2程序设计 clear;clf; axis([0,4,0,4]); hold on for r=0:0.3:3.9 x=[0.1]; for i=2:150 x(i)=r*sin(3.14*x(i-1)); end pause(0.5) for i=101:150 plot(r,x(i),'k.'); end text(r-0.1,max(x(101:150))+0.05,['\it{r}=',num2str(r)]) end 加密迭代后 clear;clf; axis([0,4,0,4]); hold on for r=0:0.005:3.9 x=[0.1]; for i=2:150 x(i)=r*sin(3.14*x(i-1)); end pause(0.1) for i=101:150 plot(r,x(i),'k.'); end end 运行后得到Feigenbaum图 2.2实验题目二 2.2.1实验问题 某农夫有一个半径10米的圆形牛栏,长满了草。他要将一头牛拴在牛栏边界的桩栏上,但只让牛吃到一半草,问拴牛鼻子的绳子应为多长? 2.2.2问题分析 如图所示,E为圆ABD的圆心,AB为拴牛的绳子,圆ABD为草场,区域ABCD为牛能到达的区域。问题要求区域ABCD等于圆ABC 的一半,可以设BC等于x,只要求出∠a和∠b就能求出所求面积。先计算扇形ABCD的面积,2a÷π×πx2=2aπ2,再求AB的面积,用扇形ABE的面积减去三角形ABE的面积即可。 数学软件与数学实验2013-2014学年度秋季学期期末试卷 专业:统计学 班级:11级2班 学号:20110723 姓名:晏静 一、按要求计算出下列表达式的值 (1)318, 3 162 53 ?? + ? ?? , 21 eπ+, 2.5 tg, 2 log15; (2)给出π的9位和e的10位近似值; (3)求658和4102的最大公约数及35和25的最小公倍数; (4)产生10个0与10之间随机数的一个表; (5)求虚数1453 i i i i +- -的实部,虚部,模,共轭,辐角。 (6)自己运用Table建立两个表,并进行表运算,如连接、并集、交、排序等操作。 二、因式分解 22212321332112322 1 22(1)()()()4;(2)21;x x x x x x x x x x x x x x x +++++---- 解: 三、解方程(组) 1234234124234-2+344-+-3(1)+31-73+3 x x x x x x x x x x x x x -=??=? ? +=??+=-? 65432(2)5232002000.x x x x x x -+--++= 四、求极限 () 20 (1)1sin ;(2);(3)56! ctg x n x n n n Lim x Lim n n →→∞ →∞++ (1) (2) (3) 五、求导数 32 22(1)()=ln(x+1+);(2)()=cos 2,; (3)=log (),Z . x f x x f f x e y x y Z xy x y y ???求的导数已知求求关于的二阶导 (1) (2) (3) 六、求下列定积分与不定积分: ()()()12201+sin ln 1+(1);(2);(3)sin (1+cos ) +1(1+)(2+-) x x dx dx x x x x x x ? ? ?2 2-(4)=0,=1,==.y D D x y y x I x e d σ??设是由直线围成的区域,计算的值 (1) (2) Matlab数学实验一——matlab初体验 一、实验目的及意义 [1] 熟悉MATLAB软件的用户环境; [2] 了解MATLAB软件的一般目的命令; [3] 掌握MATLAB数组操作与运算函数; 通过该实验的学习,使学生能熟悉matlab的基础应用,初步应用MATLAB软件解决一些简单问题。 二、实验内容 1.认识matlab的界面和基本操作 2.了解matlab的数据输出方式(format) 3. MATLAB软件的数组(矩阵)操作及运算练习; 三、实验任务 根据实验内容和步骤,完成以下具体实验,要求写出实验报告(实验目的→问题→原理→算法与编程→计算结果或图形→心得体会) 完成如下题目,并按照实验报告格式和要求填写实验报告 1.在commandwindow中分别输入如下值,看它们的值等于多少,并用matlab的help中查询这些缺省预定义变量的含义,用中文写出它们的意义。 ijeps inf nan pi realmaxrealmin 2.分别输入一个分数、整数、小数等,(如:a=1/9),观察显示结果,并使用format函数控制数据的显示格式,如:分别输入format short、format long、format short e、format long g、format bank、format hex等,然后再在命令窗口中输入a,显示a的值的不同形式,并理解这些格式的含义。 3.测试函数clear、clc的含义及所带参数的含义(利用matlab的help功能)。 4. 写出在命令窗口中的计算步骤和运行结果。 (1)计算 1.22 10 (ln log) 81 e ππ +- ; >>(log(pi)+log(pi)/log(10)-exp(1.2))^2/81 >>ans = 0.0348 (2) >> x=2;y=4; >> z=x^2+exp(x+y)-y*log(x)-3 z = 401.6562 (3)输入变量 13 5.3, 25 a b ?? ==?? ?? ,在工作空间中使用who,whos,并用save命令将变量存入”D:\exe0 1.mat”文件。测试clear命令,然后用load命令将保存的”D:\exe01.mat”文件载入>> a=5.3 a= 《数学实验》报告 实验名称 matlab拟合与插值学院机械工程学院 专业班级 姓名 学号 2011年 10月 一、【实验目的】 掌握Matlab关于采用最小二乘法拟合曲线的方法。学会使用matlab求实际中得到数据的插值曲线。 二、【实验任务】 P130第8、10、12题 三、【实验程序】 P130第8题: x=[0.10,0.30,0.40,0.55,0.70,0.80,0.95]; y=[15,18,19,21,22.6,23.8,26]; p1=polyfit(x,y,1); p3=polyfit(x,y,3); p5=polyfit(x,y,5); disp('一阶拟合函数'),f1=poly2str(p1,'x') disp('三阶拟合函数'),f3=poly2str(p3,'x') disp('五阶拟合函数'),f5=poly2str(p5,'x') x1=0.1:0.0017:0.95; y1=polyval(p1,x1); y3=polyval(p3,x1); y5=polyval(p5,x1); plot(x,y,'rp',x1,y1,'--',x1,y3,'k-.',x1,y5); legend('拟合点','一次拟合','三次拟合','七次拟合') P130第10题 x=[10,15,20,25,30]; y=[25.2,29.8,31.2,31.7,29.4]; xi=10:.5:30; yi1=interp1(x,y,xi,'*nearest'); yi2=interp1(x,y,xi,'*linear'); yi3=interp1(x,y,xi,'*spline'); yi4=interp1(x,y,xi,'*cubic'); plot(x,y,'ro',xi,yi1,'--',xi,yi2,'-',xi,yi3,'k.-',xi,yi4,'m:') ,grid on 2015-2016数学实验练习题 一、选择题 1.清除Matlab工作空间(wordspace)变量的命令是(B ) A. clc B. clear C. clf D.delete 2. 清除当前屏幕上显示的所有内容,但不清除工作空间中的数据的命令是( A ) A. clc B. clear C. clf D.delete 3. 用来清除图形的命令( C ) A. clc B. clear C. clf D.delete 4. 在MATLAB程序中,使命令行不显示运算结果的符号是( A ) A. ; B. % C. # D. & 5. 在MATLAB程序中,可以将某行表示为注释行的符号是( B ) A. ; B. % C. # D. & 6.在循环结构中跳出循环,执行循环后面代码的命令为 ( B ) A. return B. break C. continue D. Keyboard 7.在循环结构中跳出循环,但继续下次循环的命令为( C ) A. return B. break C. continue D. Keyboard 8. MATLAB中用于声明全局变量的关键字是( C ) A. inf B. syms C. global D. function 9. 用户可以通过下面哪项获得指令的使用说明( A ) A. help B. load C. demo D. lookfor 10.在MATLAB命令窗口中键入命令S=zoros(3);可生成一个三行三列的零矩阵,如果省略了变量名S,MATLAB表现计算结果将用下面的哪一变量名做缺省变量名( A ) A. ans; B. pi; C. NaN; D. Eps. 11. 9/0的结果是( B ) A. NAN; B. Inf; C. eps; D. 0 12.在MATLAB中程序或语句的执行结果都可以用不同格式显示,将数据结果显示为分数形式,用下面哪一条命令语句( D ) A. format long; B. format long e; C. format bank; D. fromat rat 13. 下列MATLAB命令中是构造1行3列的(-1,1)均匀分布随机矩阵的命令的是(D) 一、填空 1、命令clear、clf、clc、who、whos的含义分别是clear用于 清除内存中的所有变量与函数;clf用于清除图形窗口; clc用于清除命令窗口中的所有显示内容;who将内存中 的当前变量以简单的形式列出;whos列出当前内存变量 的名称、大小和类型等信息。 2、若矩阵 2310 , 5112 A B ???? == ? ? ???? ,则A.*B= (对应元素相乘)(2 0; 5 2) ,A*B=(矩阵的乘法)(5 6; 6 2)。 3、生成4行3列的元素全为1的矩阵的命令是 ones(4,3) ;生成4阶全零矩阵的命令是 zeros(4) 。生成对角线元素为[2 4 6]矩阵的命令是v=[2 4 6] A=diag(v,0) 。 4、假定A是一个6阶方阵,选取矩阵A第3行的指令是A(3,:) ,选取第4行第2列元素的指令是A(4,2) 。 5、生成一个从1到50,步长为10的等差数列构成的数组,可以使用的命令是 (from:step:to) 1:10:50 。 6、求x的平方根使用的命令是sqrt(x),round(pi)的结果 是(取整)3 7、命令subplot(2,2,2)的功能是把图形窗口分为2*2=4 个子图,并把第 2 个子图作为当前图形窗口。 8、matlab中,求解线性方程组时,矩阵行变换化简的命令是 reff 。 9、在用命令 p=polyfit (x ,y ,n )对数据进行多项式拟合时,参数n 的含义为 n 次多项式 。 10、求函数4y x cos7x =的5阶导数的命令是 diff (y ,5) 。 11、用符号法求解微分方程2xy -3y =x ,y(1)=0,y(5)=0'''的解的 指令是 dsolve(‘x*D2y-3*Dy=x^2’,’y(1)=0,y(5)=0’,’x ’) 12、Matlab 可以输入字母、汉字,但是M 文件中标点符号必须(英文) 状态下输入。 14、求x e 的命令是(exp(x)),求x 的自然对数lnx 的命令(log(x ))。 15、画图时,在x 轴旁边加注文字说明的命令是 (xlabel(‘string ’) ),图名的标注命令是(title(‘string ’)), 图例标注命令是(legend(‘string ’,’string ’,……)),在鼠标指定 位置上标注的命令是(gtext(‘string ’)),将一个图形窗口分成多 个子图的命令是(subplot(m,n,i)),画空间曲线的命令是 (plot3(x,y,z))。 16、绘制三维空间曲面图形的命令是(mesh )和(surf ),生成格 点矩阵的命令是( meshgrid ) 17、用矩形法、复合梯形公式、复合辛普生公式求12 4dx 1x +?的定积分。(详解见P150 7-28) h=0.01;x=0:h:1; y=4./(1+x.^2); format long数学软件MATLAB实验作业
Matlab数学实验报告一
MATLAB实验练习题(计算机)-南邮-MATLAB-数学实验大作业答案
MATLAB数学实验第二版答案(胡良剑)
matlab数学实验练习题
山东建筑大学数学实验期末作业matlab
MATLAB实验报告
matlab数学实验报告5
MATLAB数学实验100例题解
浅析Matlab数学实验报告
matlab与数学实验大作业
南邮MATLAB数学实验答案(全)
matlab实验报告
MATLAB数学实验报告
数学实验与数学软件(Mathmaticandmatlab)
Matlab数学实验一2015(标准答案版)
《数学实验》报告matlab-第五次作业
数学实验matlab练习题
MATLAB与数学实验练习
- Matlab数学实验一2015(标准答案版)
- (完整word版)MATLAB程序设计及应用(第二版)课后实验答案
- Matlab数学实验第二版课后习题答案
- MATLAB数学实验第二版答案(胡良剑)
- MATLAB数学实验答案(全)
- (完整版)MATLAB数学实验第二版答案(胡良剑)
- MATLAB数学实验第二版答案
- Matlab数学实验报告
- MATLAB数学实验第二版标准答案(胡良剑)
- 南邮MATLAB数学实验答案(全)
- 东华大学MATLAB数学实验第二版答案
- MATLAB数学实验第二版答案(胡良剑)
- Matlab数学实验一2015年度(答案解析版)
- Matlab数学实验一2015答案版
- Matlab数学实验报告一
- matlab数学实验习题全部答案(胡良剑)
- matlab数学实验答案(胡良剑)
- matlab数学实验作业答案
- matlab数学实验复习题(有答案)
- MATLAB数学实验报告
