数学模型(第四版)课后详细答案

数学模型作业
六道题 作业一
1.P56.8一垂钓俱乐部鼓励垂钓者将钓上的鱼放生,打算按照放生的鱼的重量给予奖励,俱乐部只准备了一把软尺用于测量,请你设计按照测量的长度估计鱼的重量的方法。假定鱼池中只有一种鲈鱼,并且得到8条鱼的如下数据(胸围指鱼身的最大周长):
解:
要求鱼的体重,我们利用质量计算公式:M=ρV 。我们假定鱼池中是同一种鱼,于是可以近似地考虑其密度是相同的。至于鱼的体积问题,由于是同一种类,可以假定这种鱼在体型上是一致的。我们假设鱼的体积和鱼身长的立方成正比。即:V=k 1L 3,因此,模型为:
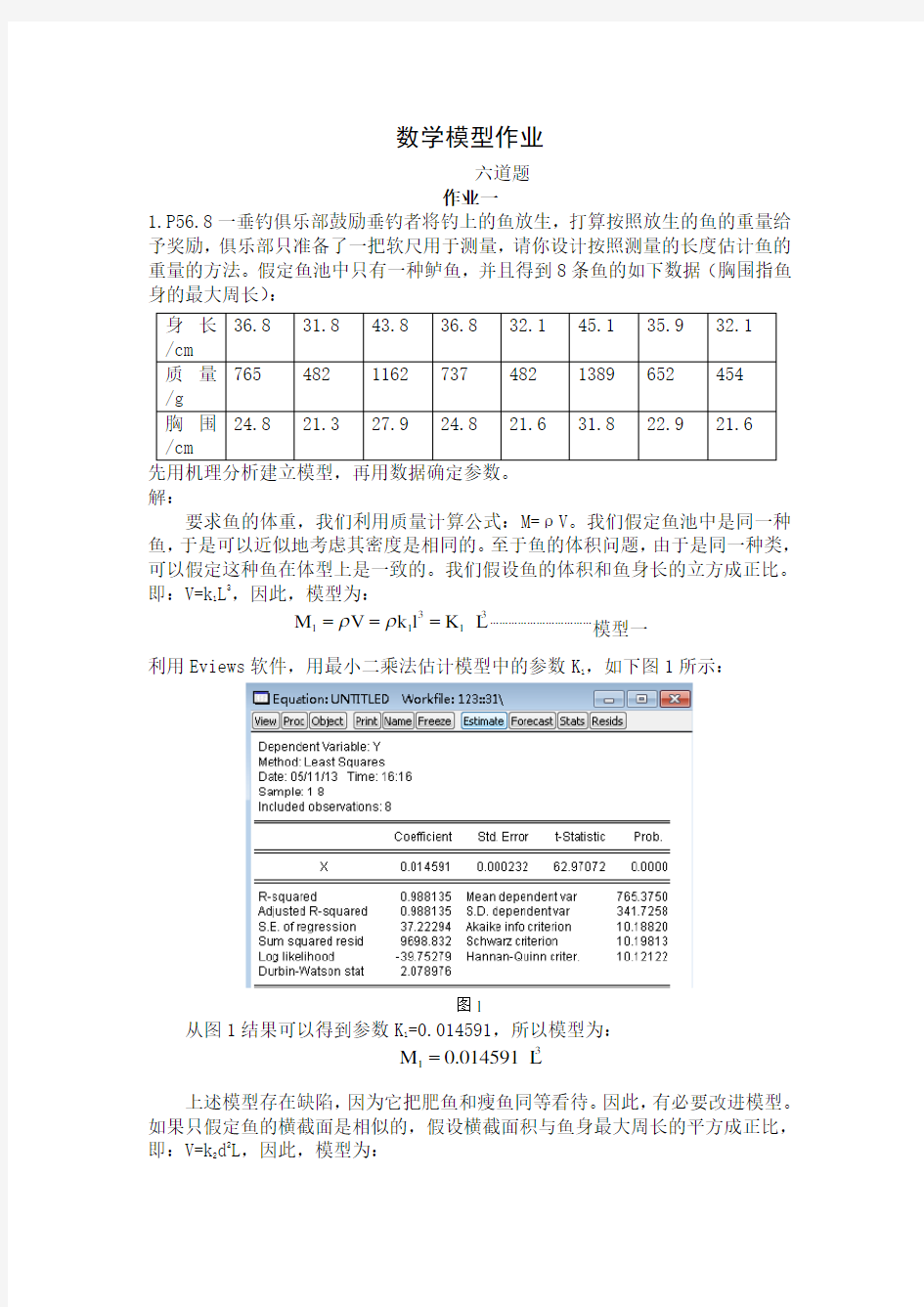
33111M V k l K L ρρ===……………………………模型一 利用Eviews 软件,用最小二乘法估计模型中的参数K 1,如下图1所示:
图1
从图1结果可以得到参数K 1=0.014591,所以模型为:
31M 0.014591 L =
上述模型存在缺陷,因为它把肥鱼和瘦鱼同等看待。因此,有必要改进模型。如果只假定鱼的横截面是相似的,假设横截面积与鱼身最大周长的平方成正比,即:V=k 2d 2L ,因此,模型为:
22222M V k d K d L L ρρ===………………………………模型二
利用Eviews 软件,用最小二乘法估计模型中的参数K 2,如下图2所示:
图2
从图2可以得到参数K 2=0. 032248,所以模型为:
22M 0.032248d L =
将实际数据与模型结果比较如表1所示:
2.P131.2 一家出版社准备在某市建立两个销售代理点,向7个区的大学生售书,每个区的大学生数量(单位:千人)已经表示在图上。每个销售代理点只能向本区和一个相邻区的大学生售书,这两个代理点应该建在何处,才能使所能供应的大学生的数量最大?建立该问题的整数线性规划模型并求解。
解:
将大学生数量为34、29、42、21、56、18、71的区分别标号为1、2、3、4、5、6、7区,画出如下区域区之间的相邻关系:
记r 为第i 区的大学生人数,用0-1变量x ij =1表示(i ,j )区的大学生由一个代售点供应图书(i i j ij i.j Max r r x s.t.2 1,{0,1} i j i j ij j j i j x x x i x =+≤+≤?∈∑∑∑∑相邻 () 即: 12132325344546566747121323242534454647566712131223242513233424455646Max 63*x 76*x 71*x 85*x 63*x 77*x 39x *x 74*x 89*x 92*x s.t.x x x x x x x x x x x 2 x x 1 x x x x 1 x x x 1 x x x 1 x =+++++++++++++++++++≤+≤+++≤++≤++≤5667ij ij x x 1 x 0x 1 ++≤==或将上述建立的模型输入LINGO ,如下: modle: max=63*x12+76*x13+71*x23+85*x25+63*x34+77*x45+39x*x46+74*x56+89*x67+92*x47 s.t. x12+x13+x23+x24+x25+x34+x45+x46+x47+x56+x67<=2; x12+x13<=1; x12+x23+x24+x25<=1; x13+x23+x34<=1; x24+x45+x56<=1; x46+x56+x67<=1 @gin(x12); @gin(x13); @gin(x23); @gin(x25); @gin(x34); @gin(x45); @gin(x46);@gin(x47); @gin(x67); End 运行,得到的输出如下: Local optirnal solution found at iteration Objective value: Vauable Value Reduced Cost x12 0.000000 0000000 x13 0.000000 0000000 x23 0.000000 0000000 x24 0.000000 0000000 x25 1.000000 0000000 x34 0.000000 0000000 x45 0.000000 0000000 x46 0.000000 0000000 x47 1.000000 0000000 x56 0.000000 0.000000 x67 0.000000 0000000 从上述结果可以得到:最优解 2547x x 1==(其他的均为0),最优值为177人. 即:第2、5区的大学生由一个销售代理点供应图书,代理点在2区或者5区,第4、7区区的大学生由另一个销售代理点供应图书,代理点在4区或者7区。 作业二 3.P181.14 在鱼塘中投放n 0尾鱼苗,随着时间的增长,尾数将减少而每尾的重量将增加。 (1)设尾数n(t) 的(相对)减少率为常数;由于喂养引起的每尾鱼重量的增加率与鱼表面积成正比,由于消耗引起的每尾鱼重量的减少率与重量本身成正比。分别建立尾数和每尾鱼重的微分方程,并求解。 (2)用控制网眼的办法不捕小鱼,到时刻T 才开始捕捞,捕捞能力用尾数的相对减少量|?/n| 表示,记作E ,即单位时间捕获量是En(t)。问如何选择T 和E ,使从T 开始的捕获量最大。 解: (1) 鱼塘的初始鱼苗为n 0尾,且随着时间的增长,尾数将减少。设尾数n(t) 的(相对)减少率为为k 1,因此由题意建立微分方程为: ,(0)(0)dn kn k dt n n =->= 求解得: 0()kt n t n e -= 在鱼塘里,由于喂养引起的每尾鱼重量的增加率与鱼表面积成正比,即: S αI(t)= 在鱼塘里,由于消耗引起的每尾鱼重量的减少率与重量本身成正比,即: m βD(t)= 所以每尾鱼重量的净增长率r(t)为: S m αβ-r(t)= 因此,建立微分方程为: dm S m dt αβ-= 因为该微分方程涉及多个变量间的数量关系,所以我们暂时无法求解该微分方程。但是要想解决此微分方程还需要更多的信息,例如,每尾鱼表面积与其重量间的关系,一旦此关系确定,便可轻松解出每尾鱼的质量随时间的变化,即m(t)。 (2) 用控制网眼的办法不捕小鱼,假设t=T 时开始捕捞,且单位时间的捕捞率为E ,依题意建立微分方程: ,()dn kn En t T dt =--≥ 因此得: ()()0()t E t T n t n e e λλ--+-= 所以单位时间的捕捞鱼的尾数为En(t),因此从T 时刻开始的总捕捞量为: ()()T y m t En t dt ∞ =? 问题就转化为求E 和λ的值,使得y 最大,由于条件不足导致m(t)求解不出,因此无法求出y 的具体解释式。 4.P213.2 雨滴的速度v 与空气密度ρ、粘滞系数μ和重力加速度g 有关,其中粘滞系数的定义是:运动物体在空气中受的摩擦力与速度梯度和接触面积的乘积成正比,比例系数为粘滞系数,用量纲分析方法给出速度v 的表达式。 解: 雨滴速度问题中涉及的物理量:雨滴的速度v ,空气密度ρ,粘滞系数μ,重力加速度g ,长度γ。要寻找的关系是: (,,,)v g ψγρμ= 更一般的将各个物理量之间的关系写作: 0),,,,(=g v f μργ 这里没有因变量与自变量之分,进而设: 3 5 1 2 4 .................(1)y y y y y v g πγρμ= 其量纲表达式为: 0130110002[]LM T []L MT ,[]L MT []LM T []LM T g νρμγ-----=====,,, 其中L ,M ,T 是基本量纲。 因此量纲表达式可以写成: 5120000130110002(LM T )(L MT )(L MT (LM T (LM T )y y y L M T -----=34 y y )) 根据量纲原则可写成: ??? ? ?=---=+=+--+0200 35414354321y y y y y y y y y y 量纲矩阵为: 1131 1()001 10()10012()()()() ()()L A M T v g γρμ--????=????---?? 解得方程的基本解为: 1211(1,,0,0,)22 ......................(2)31(0,,1,1,) 22Y Y ? =--??? ?=---?? 将(2)代入(1)可得两个相互独立的无量纲量 ???==-----2/11 2/322 /12/11g g v μργ πγπ 为了得到形如(,,,)v g ?γρμ=的关系,取12()πψπ=,其中ψ是某个函数,所以(2)式为: 1/21/23/211/2()v g g γψγρμ-----= 于是: 3/211/21/21/2()()v g g ψγρμγ---= 作业三 5.P248.13 一个岛屿上栖居着食肉爬行动物和哺乳动物,又长着茂盛的植物。爬行动物以哺乳动物为食物,哺乳动物又依赖植物生存。在适当假设下建立三者关系的模型,求其平衡点。 解: )(1t x 、)(2t x 、)(3t x 分别表示植物、哺乳动物、食肉爬行动物在时刻t 的数量。假设不考虑植物、哺乳动物和食肉爬行动物对自身的阻滞增长作用。 设1r 为植物的固有增长率,而哺乳动物的存在使植物的增长率减少,设减小的程度与捕食者数量成正比,于是建立植物数量的模型: )() (21111x r x dt t dx λ-= 比例系数1λ反映了哺乳动物消耗植物的能力。 哺乳动物离开植物无法生存,设其死亡率为2r ,则哺乳动物独自存在时有: 222) (x r dt t dx -= 而植物的存在可以为哺乳动物提供食物,但是食肉爬行动物的存在使哺乳动物数量减少,设减少的程度与食肉爬行动物数量成正比,于是建立哺乳动物数量模型: )() (312222x x r x dt t dx μλ-+-= 其中比例系数2λ反映了植物对哺乳动物的供养能力,μ反映了食肉爬行动物掠取哺乳动物的能力。 食肉爬行动物离开动物无法生存,设其死亡率为3r ,则食肉爬行动物独自存在时有: 333) (x r dt t dx -= 而哺乳动物的存在可以为食肉爬行动物提供食物,于是(4)式右端应加上哺乳动物对食肉爬行动物的增长作用,设为3λ,于是建立食肉爬行动物的数量模型: )() (23333x r x dt t dx λ+-= 比例系数3λ反映了哺乳动物对食肉爬行动物的供养能力。 综上所述,建立如下微分方程组模型 ???? ?? ???+-=-+-=-=)() ()() ()() (2333331222221111x r x dt t dx x x r x dt t dx x r x dt t dx λμλλ 求得微分方程组的平衡点为 )0,,( ),0,0,0(1 1 2221λλr r P P 其中平衡解)0,0,0(1P 对是没有意义的。 6.P43 7.9 一个服务网络由k 个工作站v1,v2,…,vk 依次串接而成,当某种服务请求到达工作站vi 时, vi 能够处理的概率为 pi ,转往下一站vi+1处理的概率为 qi (i=1,2,... ,k-1,设 qk=0),拒绝处理的概率为 ri ,满足pi + qi + ri =1。试构造马氏链模型,确定到达 vi 的请求平均经过多少工作站才能获得接受或拒绝处理的结果,被接受和拒绝的概率各多大。 解: 用随机变量i X 表示第i 站对请求服务的处理方式,i X =1表示接受请求i X =2表示拒绝请求,()i ,,k =12 , 用()a i 1表示第i 站接受请求的概率,()a i 2表示第i 站拒绝请求的概率。i q 表示第i 站转移至下一站的转移概率。分析可知,第i +1站处理请求的概率和第i 站处理请求的概率以及转移概率有关,由此可得 ()( )i i i i i i a i p q q q a i r q q q +-+-+=??? +=?? 1111 211111 其中,()a p =111 ,()a r =211,由(1)可以计算出k 个站各自接受和拒绝服务请 ()i k k k a X p p q p q q p q q q --==++++1213211211 服务请求被拒绝处理的概率为 ()i k k k a X p p q p q q r q q q --==++++121321121 2 将服务请求到达工作站i v 记做状态i ,i ,,k =12 ,设v 0表示请求被拒绝,v 00 表示请求被接受,于是转移概率矩阵为: ()()() ()()() ()()()()()()()()k k k k k p r q p r p p r q k p r k k k ---?? ?????????? =??? ??? -?? ??-???? 111221111 000010 00102010121000 转移矩阵i p =1的状态i 称为吸收状态,如果马氏链中至少含有一个吸收状态,并且从每一个非吸收状态出发,能以正的概率经有限次转移到达某一个吸收 状态,那么这个马氏链称为吸收链。吸收链可以写成简单的标准形式,若有r 个吸收状态,k r -个非吸收状态,则转移矩阵p 可表示为 r r I p R Q ??? =? ??? 0 其中k r -阶子方阵Q 的特征值λ满足λ<1,这要求子阵()k r r R -?中必含有非零元素,以满足任一非吸收状态经有限次转移能够到达某一个吸收状态的条件,这样Q 就不是随机矩阵,它至少存在一个小于1的行和,且如下定理成。由于 ()I Q -可逆因此: ()s s M I Q Q ∞ -==-=∑1 记元素全为1的列向量()T e ,,=111 ,则y Me =的第i 个分量是从第i 个非吸收状态出发,被某个吸收状态吸收的平均转移次数。 所以有 ()k k q q q q q q q q M I Q ---?? ? ??? ? ?=-=? ? ?? ???? 121112121 1101 到达i v 的请求获得接受或拒绝时,平均经过的工作站数由y Me =可得: k i q q q q q q -=++++1121211 《数学模型》作业解答 第七章( 2008 年 12 月 4 日) 1.对于节蛛网模型讨论下列问题: ( 1)因为一个时段上市的商品不能立即售完,其数量也会影响到下一时段的价格,所以第 k 1时段的价格y k 1由第k 1 和第 k 时段的数量x k 1和x k决定,如果仍设x k 1仍只取 决于 y k ,给出稳定平衡的条件,并与节的结果进行比较 . ( 2)若除了 y k 1 由 x k 1 和 x k 决定之外, x k 1 也由前两个时段的价格 析稳定平衡的条件是否还会放宽 . 解:( 1)由题设条件可得需求函数、供应函数分别为: y k 1 f x k 1 x k ) ( 2 x k 1 h( y k ) 在 P 0 (x 0 , y 0 ) 点附近用直线来近似曲线 f , h ,得到 y k 1 y 0 ( x k 1 x k x 0 ), 2 x k 1 x 0 ( y k y 0 ) , 由( 2)得 x k 2 x 0 ( y k 1 y 0 ) ( 1)代入( 3)得 x k 2 x 0 ( x k 1x k x 0 ) 2 2x k 2 x k 1 x k 2x 0 2 x 0 对应齐次方程的特征方程为 2 2 ( ) 2 8 特征根为 1, 2 4 y k 和 y k 1 确定 . 试分 (1) ( 2) (3) 当 8 时,则有特征根在单位圆外,设 8 ,则 1,2 ( ) 2 ( ) 2 8 42 2 4 1,2 1 2 即平衡稳定的条件为 2与 P 207 的结果一致 . ( 2)此时需求函数、供应函数在 P 0 (x 0 , y 0 ) 处附近的直线近似表达式分别为: y k 1 y 0 ( x k 1 x k x 0 ), ( 4) 2 x k 1 x 0 ( y k y k 1 y 0 ) , ( 5) 2 由( 5)得, (x x 0 ) β(y y y k 1 y 0 ) ( 6 ) 2 k 3 k 2 将( 4)代入( 6),得 2( x k 3 x 0 ) ( x k 2 x k 1 x 0 ) ( x k 1 x k x 0 ) 2 2 4 x k 3x k 2 2 x k 1 x k 4 x 0 4 x 0 对应齐次方程的特征方程为 4 3 2 2 0 (7) 代数方程( 7 )无正实根,且 αβ , , 2 4 不是( 7)的根 . 设( 7)的三个非零根分 别为 1, 2, 3,则 1 2 3 4 1 2 2 3 3 1 2 1 2 3 4 对( 7)作变换: , 则 12 3 q 0, p 其中 p 1 (2 2 2 ), q 1(833 2 2 ) 4 12 4 123 6 1.在3.1节存贮模型的总费用增加购买货物本身的费用,重新确定最优订货周期和订 货批量,证明在不允许缺货模型和允许缺货模型中结果都与原来的一样。 问题分析:增加购买货物本身的费用后,仍符合增加前生产规律,所以必存在一个最佳的周期,使总费用最小。 一般的考察这样的不允许缺货的存货模型:产品需求稳定不变,生产准备费和产品储存费为常数,生产能力无限,不允许缺货,确定生产周期和产量,使总费用最小。 模型假设:为了处理的方便,考虑连续模型,即设生产周期T和产量Q均为连续量。根据问题性质作如下假设: 1.产品每天的需求量为常数r 2.每件产品的购买费用为p. 3.每次生产准备费为c1,每天每件产品贮存费为c2 4.生产能力为无限大(相对于需求量),当贮存量降到零时,Q件产品立即生产 出来供给需求,即不允许缺货 模型建立:将贮存量表示为时间的函数q(t),t=0生产Q件,贮存量q(0)=Q,q(t)以需求速率递减,直到q(t)=0,如图所示 Q=rT 一个周期内的贮存费是c2∫0T q(t)dt,其中积分恰等于图中三角形A的面积QT/2,因为一个周期的准备费为c1,所以可以得到一个周期的总费用为 C=c1+c2QT/2+PQ=c1+c2rT2+prT 于是每天的平均费用为 C=C/T=c1/T+c2rT/2+pr 这就是这个优化模型的目标函数。 模型求解:求T使目标函数的C最小 C′=-c1/T2+c2r/2 令C′=0 T=√2c1/c2r 带入可得Q=√2c1r/c2 所以可以得到C=√2c1c2r 结果解释:当准备费c1增加时,生产周期和产量都变大;当贮存费c2增加时,生产周期和产量都变小;当需求量r增加时,生产周期变小而产量变大。当生产周期T=√2c1/c2r时,总费用最小。 上机练习题一 班级: 姓名: 学号: 1.建立起始值=3,增量值=5.5,终止值=44的一维数组x 答案: x=(3:5.5:44) 2.写出计算 Sin(30o )的程序语句. 答案: sin(pi*30/180) 或 sin(pi/6) 3.矩阵??????????=187624323A ,矩阵???? ??????=333222111B ;分别求出B A ?及A 与B 中对应元素之间的乘积. 答案:A = [3,2,3; 4,2,6; 7,8,1] B = [1,1,1; 2,2,2; 3,3,3] A*B ;A.*B 4计算行列式的值1 876243 23=A 。答案:det(A) 5对矩阵 ???? ??????=187624323A 进行下述操作。 (1)求秩。答案:rank(A) (2)求转置。答案:A' (3) 对矩阵求逆,求伪逆。答案:inv(A) ,pinv(A) (4) 左右反转,上下反转。答案:fliplr(A),flipud(A) (5) 求矩阵的特征值. 答案:[u,v]=eig(A) (6) 取出上三角和下三角. 答案:triu(A) tril(A) (7)以A 为分块作一个3行2列的分块矩阵。答案:repmat(a) 6 计算矩阵??????????897473535与???? ??????638976242之和。 >> a=[5 3 5;3 7 4;7 9 8]; >> b=[2 4 2;6 7 9;8 3 6]; >> a+b 7 计算??????=572396a 与?? ????=864142b 的数组乘积。 >> a=[6 9 3;2 7 5]; >> b=[2 4 1;4 6 8]; 第一部分课后习题 1.学校共1000名学生,235人住在A宿舍,333人住在B宿舍,432人住在C宿舍。学生 们要组织一个10人的委员会,试用下列办法分配各宿舍的委员数: (1)按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者。 (2)2.1节中的Q值方法。 (3)d’Hondt方法:将A,B,C各宿舍的人数用正整数n=1,2,3,…相除,其商数如 将所得商数从大到小取前10个(10为席位数),在数字下标以横线,表中A,B,C行有横线的数分别为2,3,5,这就是3个宿舍分配的席位。你能解释这种方法的道理吗。 如果委员会从10人增至15人,用以上3种方法再分配名额。将3种方法两次分配的结果列表比较。 (4)你能提出其他的方法吗。用你的方法分配上面的名额。 2.在超市购物时你注意到大包装商品比小包装商品便宜这种现象了吗。比如洁银牙膏50g 装的每支1.50元,120g装的3.00元,二者单位重量的价格比是1.2:1。试用比例方法构造模型解释这个现象。 (1)分析商品价格C与商品重量w的关系。价格由生产成本、包装成本和其他成本等决定,这些成本中有的与重量w成正比,有的与表面积成正比,还有与w无关的因素。 (2)给出单位重量价格c与w的关系,画出它的简图,说明w越大c越小,但是随着w 的增加c减少的程度变小。解释实际意义是什么。 3.一垂钓俱乐部鼓励垂钓者将调上的鱼放生,打算按照放生的鱼的重量给予奖励,俱乐部 只准备了一把软尺用于测量,请你设计按照测量的长度估计鱼的重量的方法。假定鱼池中只有一种鲈鱼,并且得到8条鱼的如下数据(胸围指鱼身的最大周长): 先用机理分析建立模型,再用数据确定参数 4.用宽w的布条缠绕直径d的圆形管道,要求布条不重叠,问布条与管道轴线的夹角 应 多大(如图)。若知道管道长度,需用多长布条(可考虑两端的影响)。如果管道是其他形状呢。 数学建模第四版答案 【篇一:数学建模课后答案】 t>第二章(1)(2012年12月21日) 1.学校共1000名学生,235人住在a宿舍,333人住在b宿舍,432人住在c宿舍.学生们 要组织一个10人的委员会,试用下列办法分配各宿舍的委员数:(1). 按比例分配取整数的名额后,剩下的名额按惯例分给小数部分 较大者; (2). 1中的q值方法; (3).d’hondt方法:将a、b、c各宿舍的人数用正整数n=1,2,3,??相除,其商数如下表: 将所得商数从大到小取前10个(10为席位数),在数字下标以横线,表中a、b、c行有横线的数分别为2,3,5,这就是3个宿舍 分配的席位.你能解释这种方法的道理吗? 如果委员会从10个人增至15人,用以上3种方法再分配名额,将 3种方法两次分配的结果列表比较. 解:先考虑n=10的分配方案, p1?235,p2?333,p3?432,方法一(按比例分配) ?p i?1 3 i ?1000. q1? p1n ?p i?1 3 ?2.35,q2? p2n i ?p i?1 3 ?3.33, q3? p3n i ?p i?1 3 ?4.32 i 分配结果为: n1?3, n2?3, n3?4 方法二(q值方法) 9个席位的分配结果(可用按比例分配)为: n1?2,n2?3, n3?4 第10个席位:计算q值为 235233324322 q1??9204.17, q2??9240.75, q3??9331.2 2?33?44?5 q3最大,第10个席位应给c.分配结果为 n1?2,n2?3,n3?5 方法三(d’hondt方法) 此方法的分配结果为:n1?2,n2?3,n3?5 此方法的道理是:记pi和ni为各宿舍的人数和席位(i=1,2,3代表a、b、c宿舍). pi 是ni 每席位代表的人数,取ni?1,2,?,从而得到的近. pip 中选较大者,可使对所有的i,i尽量接nini 再考虑n?15的分配方案,类似地可得名额分配结果.现将3种方法两次分配的结果列表如下: 2.试用微积分方法,建立录像带记数器读数n与转过时间的数学模型. 解:设录像带记数器读数为n时,录像带转过时间为t.其模型的假设见课本. 考虑t到t??t时间内录像带缠绕在右轮盘上的长度,可得 vdt?(r?wkn)2?kdn,两边积分,得 ? t vdt?2?k?(r?wkn)dn n 2?rk?wk22n2 2vv 第二章(2)(2008年10月9日) 《数学模型》作业答案 第二章(1)(2012年12月21日) 1. 学校共1000名学生,235人住在A 宿舍,333人住在B 宿舍,432人住在C 宿舍.学生们 要组织一个10人的委员会,试用下列办法分配各宿舍的委员数: (1). 按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者; (2). §1中的Q 值方法; (3).d ’Hondt 方法:将A 、B 、C 各宿舍的人数用正整数n=1,2,3,……相除,其商数如下表: 将所得商数从大到小取前10个(10为席位数),在数字下标以横线,表中A 、B 、C 行有横线的数分别为2,3,5,这就是3个宿舍分配的席位.你能解释这种方法的道理吗? 如果委员会从10个人增至15人,用以上3种方法再分配名额,将3种方法两次分配的结果列表比较. 解:先考虑N=10的分配方案, ,432 ,333 ,235321===p p p ∑==3 1 .1000i i p 方法一(按比例分配) ,35.23 1 11== ∑=i i p N p q ,33.33 1 22== ∑=i i p N p q 32.43 1 33== ∑=i i p N p q 分配结果为: 4 ,3 ,3321===n n n 方法二(Q 值方法) 9个席位的分配结果(可用按比例分配)为: 4 ,3 ,2321===n n n 第10个席位:计算Q 值为 ,17.92043223521=?=Q ,75.92404333322=?=Q 2.9331544322 3=?=Q 3Q 最大,第10个席位应给C.分配结果为 5 ,3 ,2321===n n n 方法三(d ’Hondt 方法) 此方法的分配结果为:5 ,3 ,2321===n n n 此方法的道理是:记i p 和i n 为各宿舍的人数和席位(i=1,2,3代表A 、B 、C 宿舍). i i n p 是每席位代表的人数,取,,2,1 =i n 从而得到的i i n p 中选较大者,可使对所有的,i i i n p 尽量接近. 再考虑15=N 的分配方案,类似地可得名额分配结果.现将3种方法两次分配的结果列表如下: 2. 试用微积分方法,建立录像带记数器读数n 与转过时间的数学模型. 解: 设录像带记数器读数为n 时,录像带转过时间为t.其模型的假设见课本. 考虑t 到t t ?+时间内录像带缠绕在右轮盘上的长度,可得,2)(kdn wkn r vdt π+=两边积分,得 ?? +=n t dn wkn r k vdt 0 )(2π )22 2 n wk k(r n πvt +=∴ .2 22n v k w n v rk t ππ+=∴ 《数学模型》作业解答 第三章1(2008年10月14日) 数学模型课后答案 《数学模型》作业答案 第二章(1)(2012年12月21日) 1.学校共1000名学生,235人住在A宿舍,333人住在B宿舍,432人住在C宿舍.学生们要组织一个10人的委员会,试用下列办法分配各宿舍的委员数: (1). 按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者; (2). §1中的Q值方法; (3).d’Hondt方法:将A、B、C各宿舍的人数用正整数n=1,2,3,……相除,其商数如下表: 将所得商数从大到小取前10个(10为席位数),在数字下标以横线,表中A 、B 、C 行有横线的数分别为2,3,5,这就是3个宿舍分配的席位.你能解释这种方法的道理吗? 如果委员会从10个人增至15人,用以上3种方法再分配名额,将3种方法两次分配的结果列表比较. 解:先考虑N=10的分配方案, , 432 ,333 ,235321 ===p p p ∑==3 1 . 1000i i p 方法一(按比例分配) , 35.23 1 11 == ∑=i i p N p q , 33.33 1 22 == ∑=i i p N p q 32 .43 1 33 == ∑=i i p N p q 分配结果为: 4 ,3 ,3321 ===n n n 方法二(Q 值方法) 9个席位的分配结果(可用按比例分 配)为: 4 ,3 ,2321===n n n 第10个席位:计算Q 值为 2. 试用微积分方法,建立录像带记数器读数n 与转过时间的数学模型. 解: 设录像带记数器读数为n 时,录像带转过时间为t.其模型的假设见课本. 考虑t 到t t ?+时间内录像带缠绕在右轮盘上的长度,可得,2)(kdn wkn r vdt π+=两边积分,得 ??+=n t dn wkn r k vdt 0 )(2π ) 2 2 2 n wk k(r n πvt +=∴ . 2 2 2n v k w n v rk t ππ+=∴ 《数学模型》作业解答 第三章1(2008年10月14日) 1. 在 3.1节存贮模型的总费用中增加购买货物本身的费用,重新确定最优订货周期和订货批量.证明在不允许缺货模型中结果与原来的一样,而在允许缺货模型中最优订货周期和订货批量都比原来结果减少. 第一章 4.在1、3节“椅子能在不平的地面上放稳不”的假设条件中,将四脚的连线呈正方形改为长方形,其余不变。试构造模型并求解。 答:相邻两椅脚与地面距离之与分别定义为)()(a g a f 和。f 与g 都就是连续函数。椅子在任何位置至少有三只脚着地,所以对于任意的a ,)()(a g a f 和中至少有一个不为零。不妨设0)0(,0)0(g >=f 。当椅子旋转90°后,对角线互换,0π/2)(,0)π/2(>=g f 。这样,改变椅子的位置使四只脚同时着地。就归结为证明如下的数学命题: 已 知 a a g a f 是和)()(的连续函数,对任意 0)π/2()0(,0)()(,===?f g a g a f a 且,0)π/2(,0)0(>>g f 。证明存在0a ,使0)()(00==a g a f 证:令0)π/2(0)0(),()()(<>-=h h a g a f a h 和则, 由g f 和的连续性知h 也就是连续函数。 根据连续函数的基本性质, 必存在0a (0<0a <π/2)使0)(0=a h ,即0)()(00==a g a f 因为0)()(00=?a g a f ,所以0)()(00==a g a f 8 第二章 10.用已知尺寸的矩形板材加工半径一定的圆盘,给出几种简便有效的排列方法,使加工出尽可能多的圆盘。 第三章 5.根据最优定价模型 考虑成本随着销售量的增加而减少,则设 kx q x q -=0)( (1)k 就是产量增加一个单位时成本的降低 , 销售量x 与价格p 呈线性关系0,,>-=b a bp a x (2) 收入等于销售量乘以价格p :px x f =)( (3) 利润)()()(x q x f x r -= (4) 将(1)(2)(3)代入(4)求出 ka q kbp pa bp x r --++-=02)( 当k q b a ,,,0给定后容易求出使利润达到最大的定价*p 为 b a kb ka q p 2220*+--= 第一章 课后习题6. 利用1.5节药物中毒施救模型确定对于孩子及成人服用氨茶碱能引起严重中毒和致命的最小剂量。 解:假设病人服用氨茶碱的总剂量为a ,由书中已建立的模型和假设得出肠胃中的药量为: )()0(mg M x = 由于肠胃中药物向血液系统的转移率与药量)(t x 成正比,比例系数0>λ,得到微分方程 M x x dt dx =-=)0(,λ(1) 原模型已假设0=t 时血液中药量无药物,则0)0(=y ,)(t y 的增长速度为x λ。由于治疗而减少的速度与)(t y 本身成正比,比例系数0>μ,所以得到方程: 0)0(,=-=y y x dt dy μλ(2) 方程(1)可转换为:t Me t x λ-=)( 带入方程(2)可得:)()(t t e e M t y λμμ λλ ----= 将01386=λ和1155.0=μ带入以上两方程,得: t Me t x 1386.0)(-= )(6)(13866.01155.0---=e e M t y t 针对孩子求解,得: 严重中毒时间及服用最小剂量:h t 876.7=,mg M 87.494=; 致命中毒时间及服用最小剂量:h t 876.7=,mg M 8.4694= 针对成人求解: 严重中毒时间及服用最小剂量:h t 876.7=,mg M 83.945= 致命时间及服用最小剂量:h t 876.7=,mg M 74.1987= 课后习题7. 对于1.5节的模型,如果采用的是体外血液透析的办法,求解药物中毒施救模型的血液用药量的变化并作图。 解:已知血液透析法是自身排除率的6倍,所以639.06==μu t e t x λ-=1100)(,x 为胃肠道中的药量,1386.0=λ )(6600)(t t e e t y λμ---= 1386.0,639.0,5.236)2(,1100,2,====≥-=-λλλu z e x t uz x dt dz t 解得:()2,274.112275693.01386.0≥+=--t e e t z t t 用matlab 画图: 图中绿色线条代表采用体外血液透析血液中药物浓度的变化情况。 从图中可以看出,采取血液透析时血液中药物浓度就开始下降。T=2时,血液中药物浓度最高,为236.5;当z=200时,t=2.8731,血液透析0.8731小时后就开始解毒。 第二章 1.用 2.4节实物交换模型中介绍的无差别曲线的概念,讨论以下的雇员和雇主之间的关系: 1)以雇员一天的工作时间和工资分别为横坐标和纵坐标,画出雇员无差别曲线族的示意图,解释曲线为什么是那种形状; 2)如果雇主付计时费,对不同的工资率画出计时工资线族,根据雇员的无差别曲线族和雇主的计时工资线族,讨论双方将在怎样的一条曲线上达成协议; 3)雇员和雇主已经达成了协议,如果雇主想使用雇员的工作时间增加到t 2,他有两种 数学模型作业 六道题 作业一 1.P56.8一垂钓俱乐部鼓励垂钓者将钓上的鱼放生,打算按照放生的鱼的重量给予奖励,俱乐部只准备了一把软尺用于测量,请你设计按照测量的长度估计鱼的重量的方法。假定鱼池中只有一种鲈鱼,并且得到8条鱼的如下数据(胸围指鱼身的最大周长): 解: 要求鱼的体重,我们利用质量计算公式:M=ρV。我们假定鱼池中是同一种鱼,于是可以近似地考虑其密度是相同的。至于鱼的体积问题,由于是同一种类,可以假定这种鱼在体型上是一致的。我们假设鱼的体积和鱼身长的立方成正比。即:V=k 1 L3,因此,模型为: 33 111 M V k l K L ρρ ===……………………………模型一 利用Eviews软件,用最小二乘法估计模型中的参数K 1 ,如下图1所示: 图1 从图1结果可以得到参数K 1 =0.014591,所以模型为: 3 1 M0.014591 L = 上述模型存在缺陷,因为它把肥鱼和瘦鱼同等看待。因此,有必要改进模型。如果只假定鱼的横截面是相似的,假设横截面积与鱼身最大周长的平方成 正比,即:V=k 2 d2L,因此,模型为: 身长 /cm 36.8 31.8 43.8 36.8 32.1 45.1 35.9 32.1 质量 /g 765 482 1162 737 482 1389 652 454 胸围 /cm 24.8 21.3 27.9 24.8 21.6 31.8 22.9 21.6 22222M V k d K d L L ρρ===……………………………… 模型二 利用Eviews 软件,用最小二乘法估计模型中的参数K 2,如下图2所示: 图2 从图2可以得到参数K 2=0. 032248,所以模型为: 22M 0.032248d L = 将实际数据与模型结果比较如表1所示: 实际数 据M 765 482 1162 737 482 1389 652 454 模型一M 1 727.165 469.214 1226.061 727.165 482.629 1338.502 675.108 482.619 模型二M 2 729.877 465.248 1099.465 729.877 482.960 1470.719 607.106 483.960 2.P131.2 一家出版社准备在某市建立两个销售代理点,向7个区的大学生售书,每个区的大学生数量(单位:千人)已经表示在图上。每个销售代理点只能向本区和一个相邻区的大学生售书,这两个代理点应该建在何处,才能使所能供应的大学生的数量最大?建立该问题的整数线性规划模型并求解。 解: 将大学生数量为34、29、42、21、56、18、71的区分别标号为1、2、3、4、5、6、7区,画出如下区域区之间的相邻关系: 2 5 15.速度为v 的风吹在迎风面积为s 的风车上,空气密度是ρ ,用量纲分析方法确定风车获得的功率P 与v 、S 、ρ的关系. 解: 设P 、v 、S 、ρ的关系为0),,,(=ρs v P f , 其量纲表达式为: [P]=32-T ML , [v ]=1-LT ,[s ]=2L ,[ρ]=3-ML ,这里T M L ,,是基本量纲. 量纲矩阵为: A=) ??????? ???---ρ()() ()()()()(001310013212s v P T M L 齐次线性方程组为: ?? ? ??=--=+=-++0 30 32221414321y y y y y y y y 它的基本解为)1,1,3,1(-=y 由量纲i P 定理得 1131ρπs v P -=, 1 13ρλs v P =∴ , 其中λ是无量纲常数. 16.雨滴的速度v 与空气密度ρ、粘滞系数μ和重力加速度g 有关,其中粘滞系数的定义是:运动物体在流体中受的摩擦力与速度梯度和接触面积的乘积成正比,比例系数为粘滞系 数,用量纲分析方法给出速度v 的表达式. 解:设v ,ρ,μ,g 的关系为(f v ,ρ,μ,g )=0.其量纲表达式为[v ]=LM 0T -1,[ρ]=L -3MT 0 , [μ]=MLT -2 (LT -1L -1 )-1L -2 =MLL -2T -2 T=L -1 MT -1 ,[g ]=LM 0T -2 ,其中L ,M ,T 是基本量纲. 量纲矩阵为 A=) ()()()()()() (210101101131g v T M L μρ??????????----- 齐次线性方程组Ay=0 ,即 ??? ??==+=+0 2y -y - y -0 y y 0y y -3y -y 431 324321 的基本解为y=(-3 ,-1 ,1 ,1) 由量纲i P 定理 得 g v μρπ1 3 --=. 3 ρ μλg v =∴,其中λ是无量纲常数. 对于节蛛网模型讨论下列问题: (1)因为一个时段上市的商品不能立即售完,其数量也会影响到下一时段的价格,所以第k+1时段的价格1+k y 由第k+1和第k 时段的数 量1+k x 和k x 决定。如果设1+k x 仍只取决于k y ,给出稳定平衡的条件,并 与的结果进行比较。 (2)若除了1+k y 由1+k x 和k x 决定之外,1+k x 也由前两个时段的价格k y 和 1-k y 决定,试分析稳定平衡的条件是否还会放宽。 解:(1) 设1+k y 由1+k x 和k x 的平均值决定,即价格函数表示为: )2 (11k k k x x f y +=++ 则 0),2 (0101>-+-=-++ααx x x y y k k k 0),(001>-=-+ββy y x x k k 消去y, 得到 012)1(22x x x x k k k +=++++αβαβαβ ,k=1,2,…. 该方程的特征方程为 022=++αβαβλλ 与节中 )2 (11-++=k k k y y g x 时的特征方程一样, 所以0<αβ<2, 即为0p 点的稳定条件。 (2)设 )2 (11k k k x x f y +=++ )2 (11-++=k k k y y g x , 则有 0),2 (0101>-+-=-++ααx x x y y k k k 0),2 (0101>-+=--+ββy y y x x k k k 消去y,得到 0123)1(424x x x x x k k k k +=++++++αβαβαβαβ 该方程的特征方程为 0242 3=+++αβαβλαβλλ 令λ=x,αβ=a , 即求解三次方程 0a 2ax ax 4x 2 3=+++ 的根 在matlab 中输入以下代码求解方程的根x : syms x a solve(4*x^3+a*x^2+2*a*x+a==0,x) 解得 1x = (36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(1/3)/12 - a/12 + (a*(a - 24))/(12*(36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(1/3)); 2x = -(2*a*(36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(1/3) - 3^(1/2)*a*24*i - 3^(1/2)*(36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(2/3)*i - 24*a + 3^(1/2)*a^2*i + (36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(2/3) + a^2)/(24*(36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a - 数学建模陈东彦版课后答案 篇一:数学建模承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则. 我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。如有违反竞赛规则的行为,我们将受到严肃处理。我们参赛选择的题号是(从A/B/C/D中选择一项填写):我们的参赛报名号为(如果赛区设置报名号的话):所属(请填写完整的全名):参赛队员 (打印并签名) :1.指导教师或指导教师组负责人 (打印并签名) 日期: 2010 年 11 月 22 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):对等高线图转化为三维地形图以及水的流向的探讨摘要:在等高线地形图上,根据等高线不同的弯曲形态,可以判读出地表形态的一般状况。等高线呈封闭状时,高度是外低内高,则表示为凸地形(如山峰、山地、丘顶等);等高线高度是外高内低,则表示的是凹地形(如盆地、洼地等)。等高线是曲线状时,等高线向高处弯曲的部分表示为山谷;等高线向低处凸出处为山脊。数条高程不同的等高线相交一处时,该处的地形部位为陡崖,并在图上绘有陡崖图例。由一对表示山谷与一对表示山脊的等高线组成的地形部位为鞍部。等高线密集的地方表示该处坡度较陡;等高线稀疏的地方表示该处坡度较缓。问题一:由等高线图转换为三维地形图有好多种方法,本文用坡度、坡向、等高线膨胀法以及建立空间直角坐标系的方法建立数学模型,把等高线图转化成三维地形图。问题二:把地面无限细分为无限个单元格。根据DEM栅格单元和八个相邻单元格之间的最大坡度来确定水流方向。关键字:坡度、坡向、等高线膨胀法、直角坐标系、DEM 问题一:一、问题重述:等高线能反映地表起伏的势态和地表形态的特征。随着计算机技术和图像仿真技术的发展,人们越来越需要真实的地貌环境。以前的等高线地形图上存在一些重要信息,需要还原为三维立体图形。建立数学模型,根据等高线生成三维 数学建模(I)习题 习题2 1.兔子出生后两个月就能生小兔,如果最初你养了刚出生的一雌一雄两只小兔,长成后兔子每月生一次且恰好生一雌一雄的一对,出生的小兔年内均不死,问一年后你家里共有多少对兔子?(注:本问题关系到一个十分重要的数列:菲波那奇数列) 2.有甲乙二人,乙对甲进行盯梢,甲开始时沿甲乙二人连线的垂线方向运动并一直沿此方向运动,乙的运动方向一直指向甲并与甲一直保持着d距离,求乙的运动轨迹方程。3.据观察,个子高的人一般来说腿也较长,现从16名成年女子测得数据如下表所示,请给出身高x与腿长y之间的函数关系。(单位:cm) 4.我们测量了十五个不同高度的人的体重,数据见下表。各高度的人都经适当挑选,既不太胖也不太瘦。请用这些数据建立一个体重w与身高h之间的函数关系。单位:米(身高)、公斤(体重)。 5.举重是一种一般人都能看懂的运动,它共分九个重量级,有两种主要的比赛方法:抓举和挺举。下表给出了到1977年底为止九个重量级的世界纪录。单位:公斤。 显然,运动员体重越大,他能举起的重量也越大,但举重成绩和运动员体重到底是怎样关联的呢,不同量级运动员的成绩又如何比较优劣呢?试根据这些数据建立一些经验模型并通过对它们相互之间的比较来验证一下这些模型的可信度。 6.为了检查X射线的杀菌作用,用200千伏的X射线照射细菌,每次照射6分钟,共照射15次,数据如下表所示。其中t为照射次数,y为各次照射后所剩的细菌数。请用这些数据建立y与t之间的函数关系。 表2.8 7材料不断地侵蚀,使钢包的容积不断增长。经测试,钢包的容积y 与相应的使用次数x 的数据如下表所示,请建立x 与y 之间的函数关系。单位:公斤。由于容积不便测量,容积以钢包盛满时钢水的重量来表示。 的功率p 与v 、s 、ρ的关系。 9.用量钢分析法研究人体浸在匀速流动的水里时损失的热量。记水的流速为v ,密度为ρ,比热为c ,粘性系数为μ,热传导系数为k ,人体尺寸为d 。证明人体与水的热交换系数h 与上述各物理量的关系可表示为( ,)k v d c h d k ρμ?μ=,?是未定函数,h 的定义为单位时间内在人体与水的温差为1o C 时,通过人体单位面积的流失的热量。 10.将一张四条腿的桌子放在不平的地面上,桌子的四条腿的连线呈长方形状,不允许将桌 子移到别处,但允许围绕着其中心旋转,问是否总能设法使桌子的四条腿同时落地?若桌子的四条腿共圆,结果又如何? 11.一辆汽车停于A 处并垂直于A B 方向,此汽车可转弯的最小圆半径为R ,求下列两种情况下不倒车而由A 到B 的最短路。(1)4AB R >,要求汽车到达B 点时停车方向与在 A 点时的方向相同。(2)2A B R ≥,汽车到达B 点时停车方向与A 点时的方向相反。 12.设P 是π的近似值,精度为小数点后n 位,试证明:sin()P P +是精度为3n 位的π的近似值。 13.请回答2.9节中的问题:你认为到底哪种还款方式最合算? 14.我国已经逐步实行了大学收费制度。为保障子女将来的教育费用,某家庭从他们的儿子出生时开始,每年在银行中存入若干元作为将来子女的教育基金。若年利率为10%,儿子18岁入大学后共需受教育费用约为10万元,该家庭每年应存入银行多少钱? 数学模型作业 六道题 作业一 1.P56.8一垂钓俱乐部鼓励垂钓者将钓上的鱼放生,打算按照放生的鱼的重量给予奖励,俱乐部只准备了一把软尺用于测量,请你设计按照测量的长度估计鱼的重量的方法。假定鱼池中只有一种鲈鱼,并且得到8条鱼的如下数据(胸围指鱼身的最大周长): 解: 要求鱼的体重,我们利用质量计算公式:M=ρV 。我们假定鱼池中是同一种鱼,于是可以近似地考虑其密度是相同的。至于鱼的体积问题,由于是同一种类,可以假定这种鱼在体型上是一致的。我们假设鱼的体积和鱼身长的立方成正比。即:V=k 1L 3,因此,模型为: 33111M V k l K L ρρ===……………………………模型一 利用Eviews 软件,用最小二乘法估计模型中的参数K 1,如下图1所示: 图1 从图1结果可以得到参数K 1=0.014591,所以模型为: 31M 0.014591 L = 上述模型存在缺陷,因为它把肥鱼和瘦鱼同等看待。因此,有必要改进模型。如果只假定鱼的横截面是相似的,假设横截面积与鱼身最大周长的平方成正比,即:V=k 2d 2L ,因此,模型为: 22222M V k d K d L L ρρ===………………………………模型二 利用Eviews 软件,用最小二乘法估计模型中的参数K 2,如下图2所示: 图2 从图2可以得到参数K 2=0. 032248,所以模型为: 22M 0.032248d L = 将实际数据与模型结果比较如表1所示: 2.P131.2 一家出版社准备在某市建立两个销售代理点,向7个区的大学生售书,每个区的大学生数量(单位:千人)已经表示在图上。每个销售代理点只能向本区和一个相邻区的大学生售书,这两个代理点应该建在何处,才能使所能供应的大学生的数量最大?建立该问题的整数线性规划模型并求解。 解: 将大学生数量为34、29、42、21、56、18、71的区分别标号为1、2、3、4、5、6、7区,画出如下区域区之间的相邻关系: 数学建模部分课后习题解答 中国地质大学 能源学院 华文静 1。在稳定的椅子问题中,如设椅子的四脚连线呈长方形,结论如何? 解: 模型假设 (1) 椅子四条腿一样长,椅脚与地面接触处视为一点,四脚的连线呈长方形 (2) 地面高度是连续变化的,沿任何方向都不会出现间断(没有像台阶那样的情况), 即从数学角度来看,地面是连续曲面。这个假设相当于给出了椅子能放稳的必要条件 (3) 椅子在任何位置至少有三只脚同时着地.为了保证这一点,要求对于椅脚的间距 和椅腿的长度而言,地面是相对平坦的。因为在地面上椅脚间距和椅腿长度的尺寸大小相当的范围内,如果出现深沟或凸峰(即使是连续变化的),此时三只脚是无法同时着地的. 模型建立 在上述假设下,解决问题的关键在于选择合适的变量,把椅子四只脚同时着地表示出来。首先,引入合适的变量来表示椅子位置的挪动。生活经验告诉我们,要把椅子通过挪动放稳,通常有拖动或转动椅子两种办法,也就是数学上所说的平移与旋转变换。然而,平移椅子后问题的条件没有发生本质变化,所以用平移的办法是不能解决问题的.于是可尝试将椅子就地旋转,并试图在旋转过程中找到一种椅子能放稳的情形。 注意到椅脚连线呈长方形,长方形是中心对称图形,绕它的对称中心旋转180度后,椅子仍在原地。把长方形绕它的对称中心旋转,这可以表示椅子位置的改变。于是,旋转角度θ这一变量就表示了椅子的位置。为此,在平面上建立直角坐标系来解决问题. 设椅脚连线为长方形ABCD,以对角线AC 所在的直线为x 轴,对称中心O 为原点,建立平面直角坐标系。椅子绕O点沿逆时针方向旋转角度θ后,长方形ABCD 转至A1B1C1D1的位置,这样就可以用旋转角)0(πθθ≤≤表示出椅子绕点O旋转θ后的位置。 其次,把椅脚是否着地用数学形式表示出来.当椅脚与地面的竖直距离为零时,椅脚就着地了,而当这个距离大于零时,椅脚不着地。由于椅子在不同的位置是θ的函数,因此,椅脚与地面的竖直距离也是θ的函数。 由于椅子有四只脚,因而椅脚与地面的竖直距离有四个,它们都是θ的函数,而由假设(3)可知,椅子在任何位置至少有三只脚同时着地,即这四个函数对于任意的θ,其函数值至少有三个同时为0。因此,只需引入两个距离函数即可。考虑到长方形A BCD是对称中心图形,绕其对称中心O沿逆时针方向旋转180度后,长方形位置不变,但A ,C 和B,D 对换了。因此,记A,B 两脚与地面竖直距离之和为)(θf ,C ,D两脚之和为 )(θg ,其中[]πθ,0∈,使得)()(00θθg f =成立。 模型求解 如果0)0()0(== g f ,那么结论成立。 第1 页共22 页 第一部分课后习题 1.学校共1000名学生,235人住在A宿舍,333人住在B宿舍,432人住在C宿舍。学生们要组织一个10人的委员会,试用下列办法分配各宿舍的委员数: (1)按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者。 (2)2.1节中的Q值方法。 (3)d'Hondt方法:将A,B,C各宿舍的人数用正整数n=1,2,3,…相除,其商数如下表: 234578.358.75117.5 83.25111166.5 108 216144 86.4 将所得商数从大到小取前10个(10为席位数),在数字下标以横线,表中A,B,C行有横线的数分别为2,3,5,这就是3个宿舍分配的席位。你能解释这种方法的道理吗。 如果委员会从10人增至15人,用以上3种方法再分配名额。将3种方法两次分配的结果列表比较。 (4)你能提出其他的方法吗。用你的方法分配上面的名额。 2.在超市购物时你注意到大包装商品比小包装商品便宜这种现象了吗。比如洁银牙膏50g装的每支1.50元,120g装的 3.00元,二者单位重量的价格比是1.2:1。试用比例方法构造模型解释这个现象。 (1)分析商品价格C与商品重量w的关系。价格由生产成本、包装成本和其他成本等决定,这些成本中有的与重量w成正比,有的与表面积成正比,还有与w无关的因素。 (2)给出单位重量价格c与w的关系,画出它的简图,说明w越大c越小,但是随着w的增加c减少的程度变小。解释实际意义是什么。 3.一垂钓俱乐部鼓励垂钓者将调上的鱼放生,打算按照放生的鱼的重量给予奖励,俱乐部只准备了一把软尺用于测量,请你设计按照测量的长度估计鱼的重量的方法。假定鱼池中只有一种鲈鱼,并且得到8 条鱼的如下数据(胸围指鱼身的最大周长): 方程及方程组的求解 1、路灯照明问题。在一条20m 宽的道路两侧,分别安装了一只2kw 和一只3kw 的路灯, 它们离地面的高度分别为5m 和6m 。在漆黑的夜晚,当两只路灯开启时 (1)两只路灯连线的路面上最暗的点和最亮的点在哪里? (2)如果3kw 的路灯的高度可以在3m 到9m 之间变化,如何路面上最暗点的亮度最大? (3)如果两只路灯的高度均可以在3m 到9m 之间变化,结果又如何? 解: 根据题意,建立如图模型 P1=2kw P2=3kw S=20m 照度计算公式: 2 sin r p k I α= (k 为照度系数,可取为1; P 为路灯的功率) (1)设Q(x,0)点为两盏路灯连线上的任意一点,则两盏路灯在Q 点的照度分别为 21111sin R p k I α= 22 2 22 sin R p k I α= 2 21 21 x h R += 1 1 1sin R h = α 2 22 2 2)(x s h R -+= 2 22sin R h = α Q 点的照度: 323 23 222 2 23 221 11) )20(36(18) 25(10) )((() (()(x x x s h h P x h h P x I -++ += -++ += X S P1 P2 R1 α1 α2 Q y x O R2 h1 h2 要求最暗点和最亮点,即为求函数I(x)的最大值和最小值,所以应先求出函数的极值点 5 25 25 222225 22111'))20(36()20(54)25(30))(()(3)(3)(x x x x x s h x s h P x h x h P x I -+-+ +-= -+-+ +-= 利用MATLAB 求得0)(' =x I 时x 的值 代码: s=solve('(-30*x)/((25+x^2)^(5/2))+(54*(20-x))/((36+(20-x)^2)^(5/2))'); s1=vpa(s,8); s1 运行结果: s1 = 19.97669581 9.338299136 8.538304309-11.61579012*i .2848997038e-1 8.538304309+11.61579012*i 因为x>=0,选取出有效的x 值后,利用MATLAB 求出对应的I(x)的值,如下表: x 0 0.028489970 9.3382991 19.976695 20 I(x) 0.08197716 0.08198104 0.01824393 0.08447655 0.08447468 综上,x=9.33m 时,为最暗点;x=19.97m 时,为最亮点。 (2)路灯2的高度可以变化时,Q 点的照度为关于x 和h 2的二元函数: 3 222 2 3 23 222 223 221 112) )20((3) 25(10) )(() (),(x h h x x s h h P x h h P h x I -++ += -++ += 与(1)同理,求出函数I(x,h 2)的极值即为最暗点和最亮点 0) )((3))((52222 2 2322222=-+--+=??x s h h P x s h P h I 利用matlab 求得x : solve('3/((h^2+(20-x)^2)^(3/2))-3*(3*h^2)/((h^2+(20-x)^2)^(5/2))=0') ans = 20+2^(1/2)*h 20-2^(1/2)*h 即x1=20+2^(1/2)*h (舍去) x2=20-2^(1/2)*h 0) )20(()20(9)25()220(30-))(()(3)(35222252522222522111=-+-++-=-+-++-=??x h x h x h x s h x s h P x h x h P x I 利用matlab 求解h 2数学模型第三版课后习题答案.doc
数学模型第四版习题3-1答案
数学模型习题解答解读
数学建模习题与答案课后习题
数学建模第四版答案
数学模型课后答案
数学模型课后答案
数学建模课后答案
数学建模课后习题答案
数学模型(第四版)课后详细答案
(完整版)数学模型第二章习题答案
数学模型第四版作业对于6.4节蛛网模型讨论下列问题
数学建模陈东彦版课后答案
数学建模习题2
数学模型(第四版)课后详细答案
数学建模习题答案
数学建模习题及答案
数学建模课后习题答案
