当前位置：文档库 › 微分方程作业

微分方程作业

P10习题

1.用Euler法和改进的Euler法求u’=-5u (0≤t≤1),u(0)=1的数值解，步长h=0.1,0.05;并比较两个算法的精度。

解：function du=Euler_fun1(t,u)

du=-5*u;clear;

h=0.1;tend=1;N=1/h;t(1)=0;u(1)=1;

t=h.*(0:N);

for n=1:N

u(n+1)=u(n)+h*Euler_fun1(t(n),u(n));

end

plot(t,u,'*');hold on

for n=1:N

v(1)=u(n)+h*Euler_fun1(t(n),u(n));

for k=1:6

v(k+1)=u(n)+h/2*(Euler_fun1(t(n),u(n))+Euler_fun1(t(n+1),v(k)));

end

u(n+1)=v(k+1);

end

plot(t,u,'o');

sol=dsolve('Du=-5*u','u(0)=1');

u_real=eval(sol);

plot(t,u_real,'r');

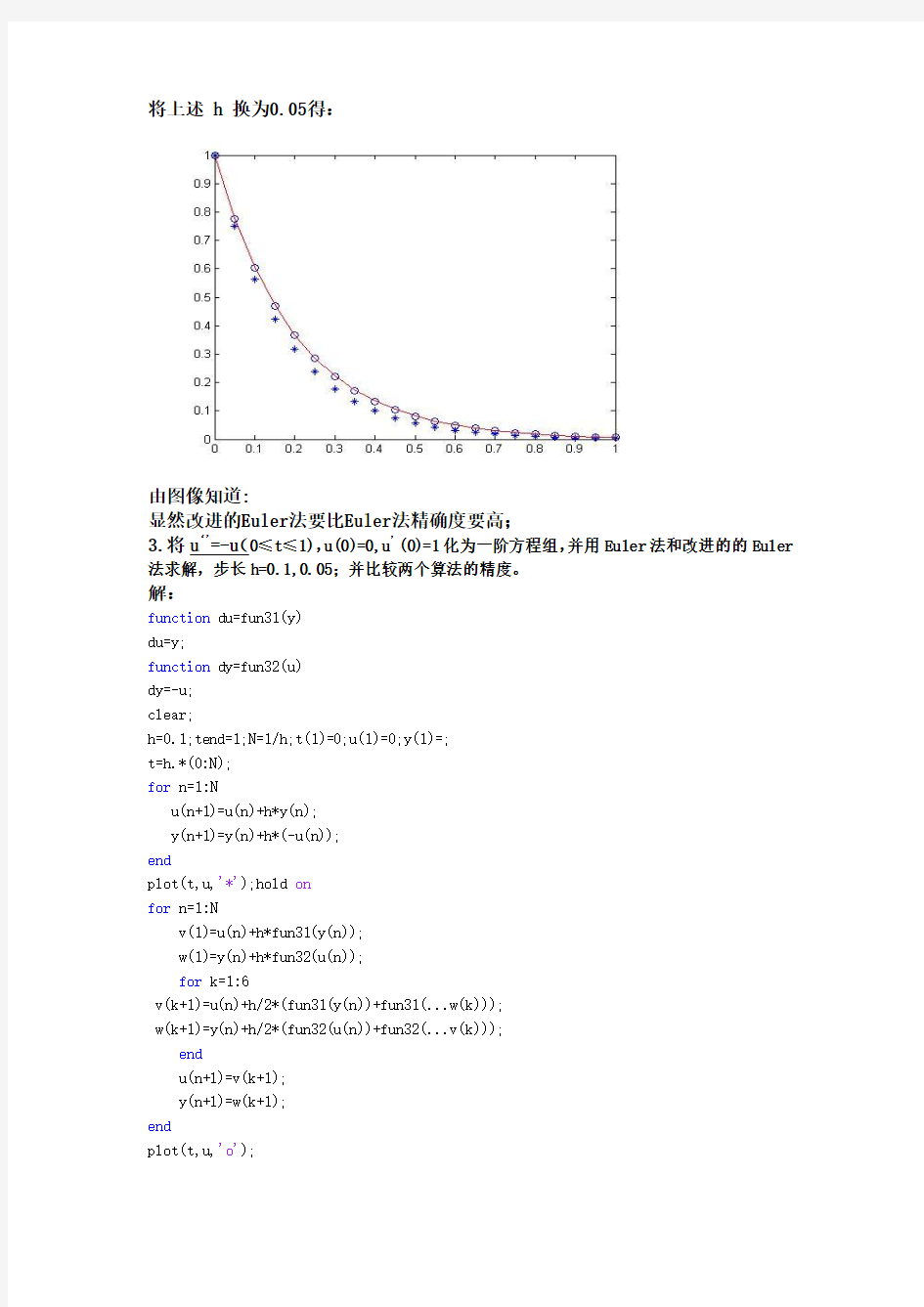
将上述 h 换为0.05得：

由图像知道:

显然改进的Euler法要比Euler法精确度要高；

3.将u‘’=-u（0≤t≤1)，u(0)=0,u’(0)=1化为一阶方程组，并用Euler法和改进的的Euler 法求解，步长h=0.1,0.05；并比较两个算法的精度。

解：

function du=fun31(y)

du=y;

function dy=fun32(u)

dy=-u;

clear;

h=0.1;tend=1;N=1/h;t(1)=0;u(1)=0;y(1)=;

t=h.*(0:N);

for n=1:N

u(n+1)=u(n)+h*y(n);

y(n+1)=y(n)+h*(-u(n));

end

plot(t,u,'*');hold on

for n=1:N

v(1)=u(n)+h*fun31(y(n));

w(1)=y(n)+h*fun32(u(n));

for k=1:6

v(k+1)=u(n)+h/2*(fun31(y(n))+fun31(...w(k)));

w(k+1)=y(n)+h/2*(fun32(u(n))+fun32(...v(k)));

end

u(n+1)=v(k+1);

y(n+1)=w(k+1);

end

plot(t,u,'o');

sol=dsolve('D2u=-u','u(0)=0','Du(0)=1';

u_real=eval(sol);

plot(t,u_real,'r');

将上述 h 换为0.05得：

由图像可以知道:

显然改进的Euler 法要比Euler 法精确度要高；

实习题（二）

1.取步长 1.0 h ，分别用Euler 法和改进的Euler 法求下列初值问题的解，并与真解相比较.

（1）????=≤<-=,

1)0(,10,'u x u u u 真解 x x u 21)(+=；

解：

function du=fun1(x,u)

du=u-2*x/u;

clear;

h=0.1;xend=1;N=1/h;x(1)=0;u(1)=1;

x=h.*(0:N);

%——Eluer 法——%

for n=1:N

u(n+1)=u(n)+h*fun1(x(n),u(n));

end

plot(x,u,'*');

hold on

%——改进的Eluer 法——%

for n=1:N

v(1)=u(n)+h*fun1(x(n),u(n));

for k=1:6

v(k+1)=u(n)+h/2*(fun1(x(n),u(n))+fun1(x(n+1),v(k)));

end

u(n+1)=v(k+1);

end

plot(x,u,'o');

hold on

%——真解——%

u_real=sqrt(1+2*x);

plot(x,u_real,'r');

由图像可以知道:

显然改进的Euler 法要比Euler 法精

确度要高；

（2）????=≤<-=,

2)1(,21,'2u x u x u 真解 3

1)ln 38()(x x x u -=；

解：

function du=fun2(x,u)

du=(u/x)-x.^2/u.^2;

clear;

h=0.1;N=1/h;x=1:h:2;x(1)=1;u(1)=2;

for n=1:N

u(n+1)=u(n)+h*fun2(x(n),u(n));

end

plot(x,u,'*');

hold on

for n=1:N

v(1)=u(n)+h*fun2(x(n),u(n));

for k=1:6

v(k+1)=u(n)+h/2*(fun2(x(n),u(n))+fun2(x(n+1),v(k)));

end

u(n+1)=v(k+1);

end

plot(x,u,'o');

hold on

u_real=x.*((8-3.*log(x)).^(1/3));

plot(x,u_real,'r');

由图像可知：

改进的Euler 法和Euler 法都很接近真值。

（3）??

??=≤<-=,1)1(,5.11,22'2u x u x u

真解 3

1223)34()(x x x u -=.

解：function du=fun3(x,u)

du=u/(2*x)-x/(2*u^2);

clear;

h=0.1;N=0.5/h;

x=1:h:1.5;

x(1)=1;u(1)=1;

for n=1:N

u(n+1)=u(n)+h*fun3(x(n),u(n));

end

plot(x,u,'*');

hold on

for n=1:N

v(1)=u(n)+h*fun3(x(n),u(n));

for k=1:6

v(k+1)=u(n)+h/2*(fun3(x(n),u(n))+fun3(x(n+1),v(k)));

end

u(n+1)=v(k+1);

end

plot(x,u,'o');

hold on

u_real=(4*x.^(3/2)-3*x.^2).^(1/3);

plot(x,u_real,'r');

由图像可以知道:

显然改进的Euler 法要比Euler 法精

确度要高；

2.试用预报校正格式(1.20)解初值问题

并与Euler 格式比较精度，取h=0.1。作业要求：写出程序，列表或用图形显示结果，并给出图或表所说明的结果。

解：

function du=Euler_fun2(t,u)

du=-u+t+1;

clear;

h=0.1;tend=1;N=1/h;t(1)=0;u(1)=1;

t=h.*(0:N);

for n=1:N

u(n+1)=u(n)+h*Euler_fun2(t(n),u(n));

end

plot(t,u,'*');

hold on

for n=1:N

u0(n+1)=u(n)+h*Euler_fun2(t(n),u(n));

u(n+1)=u(n)+h/2*(Euler_fun2(t(n),u(n))+Euler_fun2(t(n+1),u0(n+1))); end

plot(t,u,'o');

hold on

sol=dsolve('Du=-u+t+1','u(0)=1');

u_real=eval(sol);

plot(t,u_real,'r');

由图像可以知道:

显然预报校正格式要比Euler 法精确度要高；

[]010,1|1

t u u t t u ='=-++∈??=?

P37 例4.1 用四级四阶Runge-Kutta法计算初值问题：

u’=4tu0.5,0≤t≤2,

u(0)=1.

取h=0.1,0.5,1.精确解为 u(t)=(1+t2)2

作业要求：写出程序，列表或用图形显示结果，并给出图或表所说明的结果. 解：

function du=fun4(t,u)

du=4*t*u.^(1/2);

clear;

h=0.1;N=2/h;t=0:h:2;t(1)=0;u(1)=1;

for n=1:N

k1=fun4(t(n),u(n));

k2=fun4(t(n)+0.5*h,u(n)+0.5*h*k1);

k3=fun4(t(n)+0.5*h,u(n)+0.5*h*k2);

k4=fun4(t(n)+h,u(n)+h*k3);

u(n+1)=u(n)+h*(k1+2*k2+2*k3+k4)/6;

end

plot(t,u,'*');

hold on

u_real=(1+t.^2).^2;

plot(t,u_real,'r');

将上述h换为0.5后图像为：

将上述h换为1后图像为：

从上述图像来看：

第一幅图说明四级四阶Runge-Kutta法精度很高；后面两幅图说明了步长h取

的越小越逼近精确值。

常微分方程第三版答案

常微分方程第三版答案 Document serial number【KK89K-LLS98YT-SS8CB-SSUT-SST108】

习题 1． dx dy =2xy,并满足初始条件：x=0,y=1的特解。解： y dy =2xdx 两边积分有：ln|y|=x 2+c y=e 2 x +e c =cex 2另外y=0也是原方程的解，c=0时，y=0 原方程的通解为y= cex 2,x=0 y=1时 c=1 特解为y= e 2 x . 2. y 2dx+(x+1)dy=0 并求满足初始条件：x=0,y=1的特解。解：y 2dx=-(x+1)dy 2 y dy dy=-1 1+x dx 两边积分: - y 1 =-ln|x+1|+ln|c| y=|)1(|ln 1+x c 另外y=0,x=-1也是原方程的解 x=0,y=1时 c=e 特解：y= | )1(|ln 1 +x c 3．dx dy =y x xy y 321++ 解：原方程为：dx dy =y y 21+31 x x + y y 21+dy=31 x x +dx 两边积分：x(1+x 2)(1+y 2)=cx 2 4. (1+x)ydx+(1-y)xdy=0 解：原方程为： y y -1dy=-x x 1 +dx 两边积分：ln|xy|+x-y=c 另外 x=0,y=0也是原方程的解。

5．（y+x ）dy+(x-y)dx=0 解：原方程为： dx dy =-y x y x +- 令 x y =u 则dx dy =u+x dx du 代入有： -112++u u du=x 1dx ln(u 2+1)x 2=c-2arctgu 即 ln(y 2+x 2)=c-2arctg 2x y . 6. x dx dy -y+22y x -=0 解：原方程为： dx dy =x y +x x | |-2)(1x y - 则令 x y =u dx dy =u+ x dx du 2 11u - du=sgnx x 1 dx arcsin x y =sgnx ln|x|+c 7. tgydx-ctgxdy=0 解:原方程为： tgy dy =ctgx dx 两边积分：ln|siny|=-ln|cosx|-ln|c| siny= x c cos 1=x c cos 另外y=0也是原方程的解，而c=0时，y=0. 所以原方程的通解为sinycosx=c. 8 dx dy +y e x y 32 +=0 解：原方程为：dx dy =y e y 2 e x 3 2 e x 3-3e 2 y -=c.

常微分方程习题及答案

第十二章常微分方程 (A) 一、是非题 1．任意微分方程都有通解。( ) 2．微分方程的通解中包含了它所有的解。( ) 3．函数x x y cos 4sin 3-=是微分方程0=+''y y 的解。( ) 4．函数x e x y ?=2是微分方程02=+'-''y y y 的解。( ) 5．微分方程0ln =-'x y x 的通解是()C x y += 2ln 2 1 (C 为任意常数)。( ) 6．y y sin ='是一阶线性微分方程。( ) 7．xy y x y +='33不是一阶线性微分方程。( ) 8．052=+'-''y y y 的特征方程为0522=+-r r 。( ) 9． 221xy y x dx dy +++=是可分离变量的微分方程。( ) 二、填空题 1．在横线上填上方程的名称 ①()0ln 3=-?-xdy xdx y 是。 ②()()022=-++dy y x y dx x xy 是。 ③x y y dx dy x ln ?=是。 ④x x y y x sin 2+='是。 ⑤02=-'+''y y y 是。 2．x x y x y cos sin =-'+'''的通解中应含个独立常数。 3．x e y 2-=''的通解是。 4．x x y cos 2sin -=''的通解是。 5．124322+=+'+'''x y x y x y x 是阶微分方程。 6．微分方程()06 ='-''?y y y 是阶微分方程。 7．y 1 = 所满足的微分方程是。

8．x y y 2='的通解为。 9． 0=+x dy y dx 的通解为。 10．()2511 2+=+-x x y dx dy ，其对应的齐次方程的通解为。 11．方程()012=+-'y x y x 的通解为。 12．3阶微分方程3x y ='''的通解为。三、选择题 1．微分方程()043 ='-'+''y y y x y xy 的阶数是( )。 A ．3 B ．4 C ．5 D ． 2 2．微分方程152=-''-'''x y x y 的通解中应含的独立常数的个数为( )。 A ．3 B ．5 C ．4 D ． 2 3．下列函数中，哪个是微分方程02=-xdx dy 的解( )。 A ．x y 2= B ．2x y = C ．x y 2-= D ． x y -= 4．微分方程3 23y y ='的一个特解是( )。 A ．13+=x y B ．()3 2+=x y C ．()2 C x y += D ． ()3 1x C y += 5．函数x y cos =是下列哪个微分方程的解( )。 A ．0=+'y y B ．02=+'y y C ．0=+y y n D ． x y y cos =+'' 6．x x e C e C y -+=21是方程0=-''y y 的( )，其中1C ，2C 为任意常数。 A ．通解 B ．特解 C ．是方程所有的解 D ．上述都不对 7．y y ='满足2|0==x y 的特解是( )。 A ．1+=x e y B ．x e y 2= C ．2 2x e y ?= D ． x e y ?=3 8．微分方程x y y sin =+''的一个特解具有形式( )。 A ．x a y sin *= B ．x a y cos *?= C ．()x b x a x y cos sin *+= D ． x b x a y sin cos *+= 9．下列微分方程中，( )是二阶常系数齐次线性微分方程。

常微分方程练习题及答案复习题)

常微分方程练习试卷一、填空题。 1. 方程23 2 10d x x dt +=是阶（线性、非线性）微分方程. 2. 方程 ()x dy f xy y dx =经变换_______，可以化为变量分离方程 . 3. 微分方程 3230d y y x dx --=满足条件(0)1,(0)2y y '==的解有个. 4. 设常系数方程 x y y y e αβγ'''++=的一个特解*2()x x x y x e e xe =++，则此方程的系数α= ，β= ，γ= . 5. 朗斯基行列式 ()0W t ≡是函数组12(),(),,()n x t x t x t 在a x b ≤≤上线性相关的条件. 6. 方程 22(2320)0xydx x y dy ++-=的只与y 有关的积分因子为 . 7. 已知 ()X A t X '=的基解矩阵为()t Φ的，则()A t = . 8. 方程组 20'05??=???? x x 的基解矩阵为． 9.可用变换将伯努利方程化为线性方程. 10 .是满足方程 251y y y y ''''''+++= 和初始条件的唯一解. 11.方程的待定特解可取的形式: 12. 三阶常系数齐线性方程 20y y y '''''-+=的特征根是二、计算题 1.求平面上过原点的曲线方程, 该曲线上任一点处的切线与切点和点(1,0)的连线相互垂直. 2．求解方程13 dy x y dx x y +-=-+. 3. 求解方程 222()0d x dx x dt dt += 。 4．用比较系数法解方程. . 5．求方程 sin y y x '=+的通解. 6．验证微分方程 22(cos sin )(1)0x x xy dx y x dy -+-=是恰当方程，并求出它的通解.

《常微分方程》期末试卷

《常微分方程》期末试卷(16) 班级学号姓名得分评卷人一、填空题（每小题5分，本题共30分） 1．方程x x y x y e sin d d =+的任一解的最大存在区间必定是． 2．方程04=+''y y 的基本解组是． 3．向量函数组)(,),(),(21x x x n Y Y Y 在区间I 上线性相关的________________条件是在区间I 上它们的朗斯基行列式0)(=x W ． 4．李普希兹条件是保证一阶微分方程初值问题解惟一的条件． 5．n 阶线性齐次微分方程的所有解构成一个维线性空间． 6．向量函数组)(,),(),(21x x x n Y Y Y 在其定义区间I 上线性相关的条件是它们的朗斯基行列式0)(=x W ，I x ∈．得分评卷人二、计算题（每小题8分，本题共40分）求下列方程的通解 7. x y x y 2e 3d d =+ 8. 0)d (d )(3223=+++y y y x x xy x 9．0e =-'+'x y y 10．求方程x y y 5sin 5='-''的通解． 11．求下列方程组的通解． ???????+=+=y x t y y x t x 4d d d d 得分评卷人三、证明题（每小题15分，本题共30分）

12．设)(1x y ?=和)(2x y ?=是方程0)(=+''y x q y 的任意两个解，求证：它们的朗斯基行列式C x W ≡)(，其中C 为常数． 13．设)(x ?在区间),(∞+-∞上连续．试证明方程 y x x y sin )(d d ?= 的所有解的存在区间必为),(∞+-∞．

常微分方程期末试题B答案

2005——2006学年第二学期常微分方程课程试卷（B）一、填空题（每空2 分，共16分）。 1．李普希滋条件是初值问题存在唯一解的充分条件． 2. 一阶微分方程的一个特解的图像是二维空间上的一条曲线． 3．线性齐次微分方程组Y A Y ) ( d d x x =的一个基本解组的个数不能多于n个，其中R ∈ x，n R Y∈． 4．二阶线性齐次微分方程的两个解) ( 1 x y? =,) ( 2 x y? =成为其基本解组的充要条件是线性无关． 5．方程2 sin() y xy y '' =+的通解是 6．变量可分离方程()()()()0= +dy y q x p dx y N x M的积分因子是()() x P y N 1 7．性齐次微分方程组的解组) ( , ), ( ), ( 2 1 x x x n Y Y Y 为基本解组的充分必要条件是它们的朗斯基行列式0 ) (≠ x W． 8．方程540 y y y ''' ++=的基本解组是x x e e4 ,- - 二、选择题（每小题3 分，共15分）。 9．两个不同的线性齐次微分方程组（ D ）的基本解组． (A) 一定有相同(B) 可能有相同 (C) 一定有相似(D) 没有相同 10．方程组 ? ? ? ?? ? ? + = + = y x t y y x t x 4 3 d d 2 d d 的奇点)0,0(的类型是（D ）．（A）稳定焦点（B）不稳定焦点（C）鞍点（D）不稳定结点11．方程x(y2－1)d x+y(x2－1)d y=0的所有常数解是（ C ）． (A) 1± = x(B)1± = y

(C )1±=y , 1±=x (D )1=y , 1=x 12．n 阶线性非齐次微分方程的所有解（ D ）．（A ）构成一个线性空间（B ）构成一个1-n 维线性空间（C ）构成一个1+n 维线性空间（D ）不能构成一个线性空间 13．方程4d d +-=x y x y （ A ）奇解． (A) 无 (B) 有一个 (C) 有两个 (D) 可能有三、计算题（每小题8分，共48分）。 14．求方程 x y x y x y tan d d +=的通解解：令x y u =，则u x u y '+='， u x u x tan d d = 当0tan ≠u 时，等号两边积分 1d tan d C x x u u +=?? C x u ln ln sin ln += 0≠C Cx x y =sin 15．求方程0d d )1(2=+--y x x y x 的通解解：积分因子21)(x x =μ，则 0d 1d 122=+--y x x x y x 为全微分方程．取10=x ，00=y ，于是通积分为 1012 2d d 1C y x x y x y x =+--?? 即 C x x x y =++1 16．求方程2221)(x y x y y + '-'=的通解解:令 p y ='，得到2 2 2x xp p y +-= （*），两端同时关于求导，

《常微分方程》期末模拟试题

《常微分方程》模拟练习题及参考答案一、填空题（每个空格4分，共80分） 1、n 阶线性齐次微分方程基本解组中解的个数恰好是 n 个。 2、一阶微分方程 2=dy x dx 的通解为 2=+y x C （C 为任意常数），方程与通过点（2，3）的特解为 2 1=-y x ，与直线y=2x+3相切的解是 2 4=+y x ，满足条件3 3ydx =?的解为 22=-y x 。 3、李普希兹条件是保证一阶微分方程初值问题解惟一的必要条件。 4、对方程 2()dy x y dx =+作变换 =+u x y ，可将其化为变量可分离方程，其通解为 tan()=+-y x C x 。 5、方程过点共有无数个解。 6、方程 ''2 1=-y x 的通解为 42 12122=-++x x y C x C ，满足初始条件13|2,|5====x x y y 的特解为 4219 12264 =-++x x y x 。 7、方程无奇解。 8、微分方程2260--=d y dy y dx dx 可化为一阶线性微分方程组 6?=??? ?=+??dy z dx dz z y dx 。 9、方程的奇解是 y=0 。 10、35323+=d y dy x dx dx 是 3 阶常微分方程。 11、方程 22dy x y dx =+满足解得存在唯一性定理条件的区域是 xoy 平面。 12、微分方程22450d y dy y dx dx --=通解为 512-=+x x y C e C e ，该方程可化为一阶线性微分方程组 45?=??? ?=+??dy z dx dz z y dx 。 2 1d d y x y -=)1,2 (πx x y x y +-=d d y x y =d d

常微分方程习题集

《常微分方程》测试题1 一、填空题30% 1、形如的方程，称为变量分离方程，这里.分别为的连续函数。 2、形如-的方程，称为伯努利方程，这里的连续函数.n 3、如果存在常数-对于所有函数称为在R上关于满足利普希兹条件。 4、形如-的方程，称为欧拉方程，这里 5、设的某一解，则它的任一解 - 。二、计算题40% 1、求方程 2、求方程的通解。 3、求方程的隐式解。 4、求方程三、证明题30% 1.试验证=是方程组x=x,x= ，在任何不包含原点的区间a上的基解矩阵。 2.设为方程x=Ax（A为nn常数矩阵）的标准基解矩阵（即（0）=E），证明: (t)=(t- t)其中t为某一值.<%建设目标%> 《常微分方程》测试题2

一、填空题：（30%） 1、曲线上任一点的切线的纵截距是切点的横坐标和纵坐标的等差中项，则曲线所满足的 8、已知是二阶齐次线性微分方程的一个非零解，则与线性无关的另一 10、线性微分方程组的解是的基本解组的充要条件是. 二、求下列微分方程的通解：（40%） 1、 2、 3、 4、 5、求解方程．三、求初值问题的解的存在区间，并求第二次近似解，给出在解的存在区间的误差估计. （10分）

四、求解微分方程组满足初始条件的解. （10%）五、证明题：（10%）设，是方程的解，且满足==0，，这里在上连续，．试证明：存在常数C使得=C 《常微分方程》测试题3 1．辨别题指出下列方程的阶数，是否是线性方程：(12%) （1）（2）（3）（4）（5）（6） 2、填空题(8%) （1）．方程的所有常数解是___________. （2）．若y=y1(x)，y=y2(x)是一阶线性非齐次方程的两个不同解，则用这两个解可把其通解表示为________________. （3）.若方程M(x, y)d x + N(x, y)d y= 0是全微分方程，同它的通积分是 ________________. （4）.设M(x0, y0)是可微曲线y=y(x)上的任意一点，过该点的切线在x轴和y轴上的截距分别是_________________. 3、单选题(14%) （1）．方程是（）.

(整理)常微分方程试题及参考答案

常微分方程试题一、填空题(每小题3分，共39分) 1.常微分方程中的自变量个数是________. 2.路程函数S(t)的加速度是常数a，则此路程函数S(t)的一般形式是________. 3.微分方程=g( )中g(u)为u的连续函数，作变量变换________，方程可化为变量分离方程. 4.微分方程F(x,y′)=0中令P=y′,若x、P平面上的曲线F(x,P)=0的参数形式为x= (t),P=ψ(t),t为参数，则方程参数形式的通解为________. 5.方程=(x+1)3的通解为________. 6.如果函数f(x,y)连续，y= (x)是方程=f(x,y)的定义于区间x0≤x≤x0+h上，满足初始条件 (x0)=y0的解.则y= (x)是积分方程________定义于x0≤x≤x0+h 上的连续解. 7.方程=x2+xy，满足初始条件y(0)=0的第二次近似解是________. 8.方程+a1(t) +…+a n-1(t) +a n(t)x=0 中a i(t) i=1,2,…，n是〔a,b〕上的连续函数，又x1(t),x2(t),…，x n(t)为方程n 个线性无关的解，则其伏朗斯基行列式W(t) 应具有的性质是：________. 9.常系数线性方程x(4)(t)-2x″(t)+x(t)=0的通解为________. 10.设A(t)是区间a≤t≤b上的连续n×n矩阵，x1(t),x2(t),…，x n(t)是方程组 x′=A(t)x的n个线性无关的解向量.则方程组的任一解向量x(t)均可表示为：x(t)=________的形式. 11.初值问题(t)+2x″(t)-tx′(t)+3x(t)=e-t,x(1)=1,x′(1)=2,x″(1)=3 可化为与之等价的一阶方程组________. 12.如果A是3×3的常数矩阵，-2为A的三重特征值，则方程组x′=Ax的基解矩阵exp A t=________. 13.方程组的奇点类型是________. 二、计算题(共45分) 1.(6分)解方程 = . 2.(6分)解方程 x″(t)+ =0. 3.(6分)解方程 (y-1-xy)dx+xdy=0. 4.(6分)解方程

常微分方程期末考试练习题及答案

一，常微分方程的基本概念常微分方程：含一个自变量x，未知数y及若干阶导数的方程式。一般形式为：F（x，y，y，.....y(n)）=0 (n≠0). 1. 常微分方程中包含未知函数最高阶导数的阶数称为该方程的阶。如：f(x)（3）+3f(x)+x=f(x)为3阶方程。 2.若f（x）使常微分方程两端恒等，则f（x）称为常微分方程的解。 3.含有独立的任意个常数（个数等于方程的阶数）的方程的解称为常微分方程的通解。如常系数三阶微分方程F（t，x（3））=0的通解的形式为：x（t）=c1x（t）+c2x（t）+c3x（t）。 4.满足初值条件的解称为它的特解（特解不唯一，亦可能不存在）。 5.常微分方程之线性及非线性：对于F（x，y，y，......y(n)）=0而言，如果方程之左端是y，y，......y(n)的一次有理式，则次方程为n阶线性微分方程。（方程线性与否与自变量无关）。如：xy（2）-5y，+3xy=sinx 为2阶线性微分方程；y（2）+siny=0为非线性微分方程。注：a.这里主要介绍几个主要的，常用的常微分方程的基本概念。余者如常微分方程之显隐式解，初值条件，初值问题等概念这里予以略去。另外，有兴趣的同学不妨看一下教材23页的雅可比矩阵。 b.教材28页第八题不妨做做。二.可分离变量的方程 A.变量分离方程

1.定义：形如 dx dy =f （x)φ(y)的方程，称为分离变量方程。这里f （x ），φ（x ）分别是x ，y 的连续函数。 2.解法：分离变量法? ? +=c dx x f y dy )()(?. （*）说明： a 由于（*）是建立在φ（y ）≠0的基础上，故而可能漏解。需视情况补上φ（y ）=0的特解。（有时候特解也可以和通解统一于一式中） b.不需考虑因自变量引起的分母为零的情况。例1.0)4(2=-+dy x x ydx 解：由题意分离变量得：04 2=+-y dy x dx 即： 0)141(41=+--y dy dx x x 积分之，得：c y x x =+--ln )ln 4(ln 4 1 故原方程通解为：cx y x =-4)4( （c 为任意常数），特解y=0包含在通解中（即两者统一于一式中）。 *例2.若连续函数f （x ）满足 2 ln )2 ()(20 +=? dt t f x f x ，则f （x ）是？解：对给定的积分方程两边关于x 求导，得： )(2)('x f x f = （变上限求积分求导）分离变量，解之得：x Ce x f 2)(= 由原方程知： f （0）=ln2，代入上解析式得： C=ln2， B.可化为分离变量方程的类型。解决数学题目有一个显而易见的思想：即把遇到的新问题，结合已知

《常微分方程》第三次作业

《常微分方程》第三次作业第3章一阶线性微分方程组 1．完成定理3.1的证明． 2．完成定理3.1′的证明 3．将下列方程式化为一阶方程组（1）0)()(=++x g x x f x &&& （2）)(d d d d 22t f kx t x c t x m =++ （3）0)()()(321=+'+''+'''y x a y x a y x a y 4．求解方程组 ?????? ?+=+=y t p x t q t y y t q x t p t x )()(d d )()(d d 其中)(),(t q t p 在[a , b ]上连续． 5．设n n ?矩阵函数)(1t A ，)(2t A 在（a , b ）上连续，试证明，若方程组 X A X )(d d 1t t = 与X A X )(d d 12t t = 有相同的基本解组，则)(1t A ≡)(2t A ． 6．求解下列方程组：（1）???????==y t y x t x 2d d d d （2）???????+=+=x y t y x y t x 54d d 45d d （3）???????+-=+=y x t y y x t x αββαd d d d 7．求解下列方程组：（1）???-=+=x y y y x x 23&& （2）??? ??+-=-+=+-=z y x z z y x y z y x x 222&&& 8．求解下列方程组：（1）???????=+=y t y y x t x 3d d 3d d （2）???? ?????=+=+=333222 11 2d d 2d d 2d d y x y y y x y y y x y （3）?????+=+=2 e 2t x y y x t && （4）???++=++=t y x y t y x x e 823532&&

常微分方程作业答案

1.第1题设就是n 阶齐次线性方程的线性无关的解, 其中就是连续函数、则 A、的朗斯基行列式一定就是正的; B、的朗斯基行列式一定就是负的; C、的朗斯基行列式可有零点, 但不恒为零; D、的朗斯基行列式恒不为零、 A、A B、B C、C D、D 您的答案:B 题目分数:2 此题得分:2、0 2.第2题满足初始条件与方程组的解为 ( )、 A、; B、 ; C、 ; D、、

A、、 B、、 C、、 D、、您的答案:B 题目分数:2 此题得分:2、0 3.第6题下列四个微分方程中, 三阶常微分方程有( )个、 (i) , (ii) , (iii) , (iv) 、 A、1 B、2 C、3 D、4 您的答案:C 题目分数:2 此题得分:2、0 4.第8题就是某个初值问题的唯一解,其中方程就是, 则初始条件应该就是( )、 A、,

B、, C、, D、、 A、A B、B C、C D、D 您的答案:A 题目分数:2 此题得分:2、0 5.第9题可将一阶方程化为变量分离方程的变换为 A、; B、 ; C、; D、、 A、、 B、、 C、、 D、、您的答案:C 题目分数:2 此题得分:2、0 6.第15题

可将六阶方程化为二阶方程的变换就是( )、 A、; B、 ; C、 ; D、、 A、、 B、、 C、、 D、、您的答案:B 题目分数:2 此题得分:2、0 7.第16题设,及就是连续函数,与就是二阶变系数齐次线性方程的两个线性无关的解, 则以常数变易公式作为唯一解的初值问题就是

A、B、 C、D、 A、、 B、、 C、、 D、、您的答案:B 题目分数:2 此题得分:2、0 8.第18题设与就是方程组的两个基解矩阵, 则 A、存在某个常数方阵C使得, 其中; B、存在某个常数方阵C使得, 其中 ; C、存在某个常数方阵C使得, 其中; D、存在某个常数方阵C使得, 其中、 A、、 B、、

2018常微分方程考研复试真题及答案

常微分方程计算题 2.指出下列方程中的阶数，是线性方程还是非线性方程，并说明理由；（1） t 2 2 2dt u d +t dt du +( t 2 -1)u=0 （2） dx dy =x 2+y 2 ; （3）dx dy + 2 x y =0 3.求曲线族y=C 1e x +C 2x e x 所满足的微分方程 4．验证函数y= C 1e x 2+ C 2e x 2-是微分方程y `` -4y=0的解，进一步验证它是通解。 5.试用一阶微分方程形式不变性求解方程dx dy =2x 6.什么叫积分一个微分方程 7．什么是求解常微分方程的初等积分法 8．分离变量一阶方程的特征是什么 9．求下列方程的通解（1） y ` ＝sinx （2） x 2 y 2 y ` +1=y （3） tgx dx dy =1+y （4） dx dy =exp(2x-y) （5） dx dy =21y 2- （6） x 2 ydx=(1- y 2 +x-2 x 2 y 2 )dx （7）( x 2 +1)( y 2 -1)dx+xydy=0 10.叙述齐次函数的定义 11．试给出一阶方程y ` ＝f(x,y)或p(x,y)dx+ q(x,y)dy=0为齐次方程的特征。说明二

个方程的关系。 12．求解齐次方程通常用什么初等变换，新旧函数导数关系如何 13．求解下列方程 dx dy ＝2 22y x xy - 14．求解下列方程（1）（x+2y ）dx —xdy=0 (2) dx dy =x y +y x 2 15. dx dy =22y x xy + 16(x 2 +y 2 )dx —2xydy=0 17. dx dy =5 242+---y x x y 18―――――19 20―――――――27

常微分方程课后答案(第三版)王高雄

习题2.2 求下列方程的解。 1．dx dy =x y sin + 解： y=e ?dx (?x sin e ?-dx c dx +) =e x [- 2 1e x -(x x cos sin +)+c] =c e x -21 (x x cos sin +)是原方程的解。 2．dt dx +3x=e t 2 解：原方程可化为： dt dx =-3x+e t 2 所以：x=e ?-dt 3 (?e t 2 e -? -dt 3c dt +) =e t 3- (5 1e t 5+c) =c e t 3-+5 1e t 2 是原方程的解。 3．dt ds =-s t cos +21t 2sin 解：s=e ?-tdt cos (t 2sin 2 1?e dt dt ?3c + ) =e t sin -(?+c dt te t t sin cos sin ) = e t sin -(c e te t t +-sin sin sin ) =1sin sin -+-t ce t 是原方程的解。 4． dx dy n x x e y n x =- ， n 为常数. 解：原方程可化为：dx dy n x x e y n x += )(c dx e x e e y dx x n n x dx x n +??=?- )(c e x x n += 是原方程的解.

5． dx dy +1212--y x x =0 解：原方程可化为：dx dy =-1212+-y x x ?=-dx x x e y 1 2(c dx e dx x x +?-221) )21(ln 2+=x e )(1 ln 2?+--c dx e x x =)1(1 2 x ce x + 是原方程的解. 6． dx dy 234xy x x += 解：dx dy 234xy x x += =23y x +x y 令 x y u = 则 ux y = dx dy =u dx du x + 因此：dx du x u +=2u x 21u dx du = dx du u =2 c x u +=33 1 c x x u +=-33 （*）将x y u =带入（*）中得：3433cx x y =-是原方程的解.

秋华师《常微分方程》在线作业

————————————————————————————————作者：————————————————————————————————日期:

奥鹏1７春16秋华师《常微分方程》在线作业一、单选题（共20 道试题，共60 分。）１. 微分方程ｙ''+y=sinx的一个特解具有形式()。 A. y*=asinx B．y＊＝acosx C．ｙ*=x(ａsiｎｘ＋bcosx) D．y*＝acｏsx+bｓinx 正确答案: 2. y'''+ｓｉnxy＇-ｘ=cｏsx的通解中应含(）个独立常数。 A. １ B. 2 C．3 D. ４正确答案： 3．微分方程xyy''+x（y')^3-y^4-ｙ'＝0的阶数是()。 A. 3 B. 4 C. 5 Ｄ. 2 正确答案：４．微分方程ｙ'''-ｘ^2ｙ'＇-x^5＝１的通解中应含的独立常数的个数为（)。 A. 3 B. 5 C. 4 D． 2 正确答案： 5. 过点(１,3)且切线斜率为2x的曲线方程y=ｙ(x)应满足的关系是（）。 A.y'＝2x B. ｙ''＝２ｘ C. y＇＝2x,y(１)=３Ｄ. ｙ''＝2x,ｙ(1）＝3 正确答案：６.方程dy/ｄx=3y（2/３)过点(0，0）有（)． A. 无数个解 B. 只有一个解 C．只有两个解 D．只有三个解

正确答案：７. 方程y'-２y=0的通解是（)。 A. y＝sinx B. y=4e^(２ｘ) C．ｙ=Ce^(2ｘ) Ｄ．ｙ=ｅ^x 正确答案： 8. 下列函数中,是微分方程y＇'-7y'+1２ｙ＝0的解()。Ａ. y=ｘ^３ B. y=x^2 C. ｙ=e^(3x) D．y=ｅ^（2x) 正确答案： 9．按照微分方程通解定义,ｙ＇'=sinx的通解是()。 A. -sｉnｘ+C1x+C2 Ｂ. －ｓinx+C1+Ｃ2 Ｃ. siｎx+C１ｘ＋C2 D．ｓinx+C１x+C2 正确答案: 10．方程组dY/ｄx＝F(x,Y),ｘ∈R，Y∈R^n的任何一个解的图象是（）维空间中的一条积分曲线. A. n B.n+１ C．n-1 D. n－２正确答案: 1１．下列函数中，哪个是微分方程dｙ-２ｘdx=0的解（)。 A. y=2x Ｂ．y=x^2 C. ｙ=-2x D．y=－x 正确答案：１２. 微分方程cosｙdy=ｓｉnxdx的通解是()。Ａ. sinｘ+cｏsｘ=C B．ｃosｙ-ｓinx=Ｃ C. cosｘ－siny＝C D.cｏｓx+sinｙ=C 正确答案: 13. 微分方程2ydｙ-ｄx=0的通解为（)。 A. y^2-x=C B. ｙ-x＾(１/2)＝C C. y=x+C D. y＝-x+C 正确答案：

常微分方程应用题和答案

应用题（每题10分） 1、设()f x 在(,)-∞∞上有定义且不恒为零，又()f x '存在并对任意,x y 恒有 ()()()f x y f x f y +=，求()f x 。 2、设()()()F x f x g x =，其中函数(),()f x g x 在(,)-∞∞内满足以下条件 ()(),()(),(0)0,()()2x f x g x g x f x f f x g x e ''===+= （1）求()F x 所满足的一阶微分方程；（2）求出()F x 的表达式。 3、已知连续函数()f x 满足条件320 ()3x x t f x f dt e ??=+ ??? ?，求()f x 。 4、已知函数()f x 在(0,)+∞内可导，()0,lim ()1x f x f x →+∞ >=，且满足 1 1 0()lim ()h x h f x hx e f x →? ?+ ?= ? ?? ? ，求()f x 。 5、设函数()f x 在(0,)+∞内连续，5 (1)2 f =，且对所有,(0,)x t ∈+∞，满足条件 1 1 1 ()()()xt x t f u du t f u du x f u du =+? ??，求()f x 。 6、求连续函数()f x ，使它满足10 ()()sin f tx dt f x x x =+?? 。 7、已知可微函数()f t 满足 31() ()1()x f t dt f x t f t t =-+?，试求()f x 。 8、设有微分方程 '2()y y x ?-=，其中21 ()01x x x ?? 。试求在(,)-∞∞内的连续函数()y y x =使之在(,1)-∞和()1,+∞内部满足所给方程，且满足条件(0)0y =。 9、设位于第一象限的曲线()y f x = 过点122?? ? ? ?? ，其上任一点(,)P x y 处的法线与y 轴的交点为Q ，且线段PQ 被x 轴平分。（1）求曲线()y f x =的方程；（2）已知曲线sin y x =在[0,]π上的弧长为l ，试用l 表示曲线()y f x =的弧长s 。 10、求微分方程(2)0xdy x y dx +-=的一个解()y y x =，使得由曲线()y y x =与直线 1,2x x ==以及x 轴所围成的平面图形绕x 轴旋转一周的旋转体体积最小。 11、设曲线L 位于xOy 平面的第一象限内，L 上任一点M 处的切线与y 轴总相交，交点记为

常微分方程作业答案

1．第1题设是n 阶齐次线性方程的线性无关的解, 其中是连续函数. 则 A. 的朗斯基行列式一定是正的; B. 的朗斯基行列式一定是负的; C. 的朗斯基行列式可有零点, 但不恒为零; D. 的朗斯基行列式恒不为零. 您的答案：B 题目分数：2 此题得分： 2．第2题满足初始条件和方程组的解为 ( ). A. ; B. ; C. ; D. . A.. B.. C.. D.. 您的答案：B 题目分数：2 此题得分： 3．第6题下列四个微分方程中, 三阶常微分方程有( )个. (i) , (ii) ,

(iii) , (iv) . 您的答案：C 题目分数：2 此题得分： 4．第8题是某个初值问题的唯一解，其中方程是, 则初始条件应该是( ). A. , B. , C. , D. . 您的答案：A 题目分数：2 此题得分： 5．第9题可将一阶方程化为变量分离方程的变换为 A. ； B. ； C. ； D. . A..

B.. C.. D.. 您的答案：C 题目分数：2 此题得分： 6．第15题可将六阶方程化为二阶方程的变换是( ). A.; B. ; C.; D.. A.. B.. C.. D.. 您的答案：B 题目分数：2 此题得分： 7．第16题设，及是连续函数，和是二阶变系数齐次线性方程的两个线性无关的解, 则以常数变易公式作为唯一解的初值问题是 A. B. C. D. A.. B.. C.. D.. 您的答案：B 题目分数：2

此题得分： 8．第18题设和是方程组的两个基解矩阵, 则 A. 存在某个常数方阵C使得, 其中; B. 存在某个常数方阵C使得, 其中; C. 存在某个常数方阵C使得, 其中; D. 存在某个常数方阵C使得, 其中. A.. B.. C.. D.. 您的答案：A 题目分数：2 此题得分： 9．第20题微分方程的一个解是( ). A. , B. , C. , D. . A.. B.. C.. D.. 您的答案：D 题目分数：2 此题得分： 10．第22题设有四个常微分方程： (i) , (ii) , (iii) , (iv) .

常微分方程习题

第一章习题 1-1求下列两个微分方程的公共解。（1）422x x y y -+=' （2）2422y y x x x y --++=' 解两方程的公共解满足条件 4224222x x y y y x x x -+=--++，即 022224=-+-y x y x ， 0))(122(22=-++y x y x ，所以2 x y =或2212 x y +-=。代入检验可知2 212 x y +-=不符合，所以两方程的公共解为2x y =。评注：此题是求解方程满足一定条件的解，即求两个微分方程的公共解。在求解时由于令其导数相等，很容易产生增解，因而要对所求结果回代原方程进行检验，舍去增解。 1-2 求微分方程02 =-'+'y y x y 的直线积分曲线。解设直线积分曲线为b ax y +=，则a y ='，代入原方程得 02≡--+b ax xa a ，即0)()(2 ≡-+-b a a a x ，所以 ???=-=-0 02b a a a ，可得0==b a 或1==b a 。因而所求直线积分曲线为0=y 或1+=x y 。评注：此题是求解方程的部分解，采用的是待定系数法。待定系数法是求解常微分方程常用的方法之一，有待定常数法和待定函数法。本题首先设出满足题设条件的含有待定常数

的解，然后代入原方程来确定待定常数，解决此类问题的关键在于正确地设出解的形式。 1-3 微分方程32224xy y y x =-'，证明其积分曲线是关于坐标原点成中心对称的曲线。证设)(x y ?=满足微分方程，只须证明)(x y --=?也满足方程即可。作变换x t -=，则证明)(t y ?-=满足方程即可，代入方程两端，并利用)(x y ?=满足此方程，得左=)())((42222t dx dt t t ??-'， )()1)((42222t t t ??--'= )()(4222t t t ??-'=)(3t t ?==右故)(t y ?-=也满足方程32224xy y y x =-'。评注：为了验证)(x y --=?也满足方程，利用积分曲线的性质，进行变量代换x t -=，将)(x y --=?变换成)(t y ?-=后，问题就很容易解决了。 1-4 物体在空气中的冷却速度与物体和空气的温差成正比，如果物体在20分钟内由100℃冷却至60℃，那么，在多长时间内，这个物体由100℃冷却至30℃？假设空气的温度为20℃ 解设物体在空气中时刻t 的温度为)(t T T =，则依牛顿冷却定理得 )20(--=T k dt dT ，其中k 是比例常数。两边积分，得通解为kt Ce T -+=20。由于初始条件为：,100)0(=T 故得80=C ，所以kt e T -+=8020。将60,20==T t 代入上式后即得：202ln = k ，即 20202ln )2 1(80208020t t e T ?+=+=-。故当30=T 时，有20)2 1(802030t ?+=，从中解出60=t （分钟），因此，在一小时内，可使物体由100℃冷却至30℃。

(完整版)常微分方程期末考试试卷(6)

常微分方程期末考试试卷(6) 学院 ______ 班级 _______ 学号 _______ 姓名 _______ 成绩 _______ 一．填空题（共30分，9小题，10个空格，每格3分）。 1.当_______________时，方程M(x,y)dx+N(x,y)dy=0称为恰当方程，或称全微分方程。 2、________________称为齐次方程。 3、求dx dy =f(x,y)满足00)(y x =?的解等价于求积分方程____________________的连续解。 4、若函数f(x,y)在区域G 内连续，且关于y 满足利普希兹条件，则方程),(y x f dx dy = 的解 y=),,(00y x x ?作为00,,y x x 的函数在它的存在范围内是__________。 5、若)(),...(),(321t x t x t x 为n 阶齐线性方程的n 个解，则它们线性无关的充要条件是__________________________________________。 6、方程组x t A x )(/=的_________________称之为x t A x )(/=的一个基本解组。 7、若)(t φ是常系数线性方程组Ax x =/的基解矩阵，则expAt =____________。 8、满足___________________的点（**,y x ），称为方程组的奇点。 9、当方程组的特征根为两个共轭虚根时，则当其实部________时，零解是稳定的，对应的奇点称为___________。二、计算题（共6小题，每题10分）。 1、求解方程：dx dy =3 12+++-y x y x 2.解方程： (2x+2y-1)dx+(x+y-2)dy=0

微分方程作业

常微分方程第三版答案

常微分方程习题及答案

常微分方程练习题及答案复习题)

《常微分方程》期末试卷

常微分方程期末试题B答案

《常微分方程》期末模拟试题

常微分方程习题集

(整理)常微分方程试题及参考答案

常微分方程期末考试练习题及答案

《常微分方程》第三次作业

常微分方程作业答案

2018常微分方程考研复试真题及答案

最新常微分方程期末考试题大全(东北师大)

常微分方程课后答案(第三版)王高雄

秋华师《常微分方程》在线作业

常微分方程应用题和答案

常微分方程作业答案

常微分方程习题

(完整版)常微分方程期末考试试卷(6)