2013高三一轮复习之函数的性质(一)概念,定义域,值域,解析式)函数基础1

授课类型

T 函数的概念 C 函数的定义域与值域 T 函数的解析式

T 函数的概念

知识梳理

一、函数的基本概念： 1、函数定义：

设A ，B 是非空的数集 ，如果按照某种确定的对应关系f ,使对于集合A 中的 任意 一个数x ,在集合B 中都有 唯一确定 的数()f x 和它对应，那么就称f : A →B 为从集合A 到集合B 的一个函数，记作

()y f x x A =∈，.

2、函数的三要素： 定义域 、 值域 和 对应关系 .

3、相等函数：如果两个函数的 定义域 和 对应关系 完全一致，则这两个函数相等，这是判断两函数相等的依据.

注：若两个函数的定义域与值域相同，是否为相等函数？

（不一定。如果函数y x =和1y x =+,其定义域与值域完全相同，但不是相等函数；再如sin y x =与

cos y x =，其定义域为R ，值域都为[1,1]-，显然不是相等函数。因此看两个函数是否相等，关键是看定义域

和对应关系）

二、函数的表示法： 表示函数的常用方法有： 解析法 、 图象法 、 列表法 .

三、函数的定义域、值域：

在函数()y f x x A =∈，,中，x 叫做自变量，x 的取值范围A 叫做函数的定义域 ；与x 的值相对应的y 值叫做函数值，函数值的集合{()f x |x A ∈}叫做函数的值域 .

函数的定义域包含三种形式：

①自然型：指函数的解析式有意义的自变量x 的取值范围（如：分式函数的分母不为零，偶次根式函数的被开方数为非负数，对数函数的真数为正数，等等）；

②限制型：指命题的条件或人为对自变量x 的限制，这是函数学习中重点，往往也是难点，因为有时这种限制比较隐蔽，容易犯错误；

③实际型：解决函数的综合问题与应用问题时，应认真考察自变量x 的实际意义。

常见简单函数的值域求法：

①配方法（将函数转化为二次函数）；②判别式法（将函数转化为二次方程）；③不等式法（运用不等式的各种性质）；④函数法（运用基本函数性质，或抓住函数的单调性、函数图象等），⑤数形结合法（将函数的值域问题转化为具有几何意义的变量，求解其取值关系），等等。 四、分段函数

若函数在其定义域的不同子集上，因对应法则不同而分别用几个不同的式子来表示，这种函数称为分段函数。

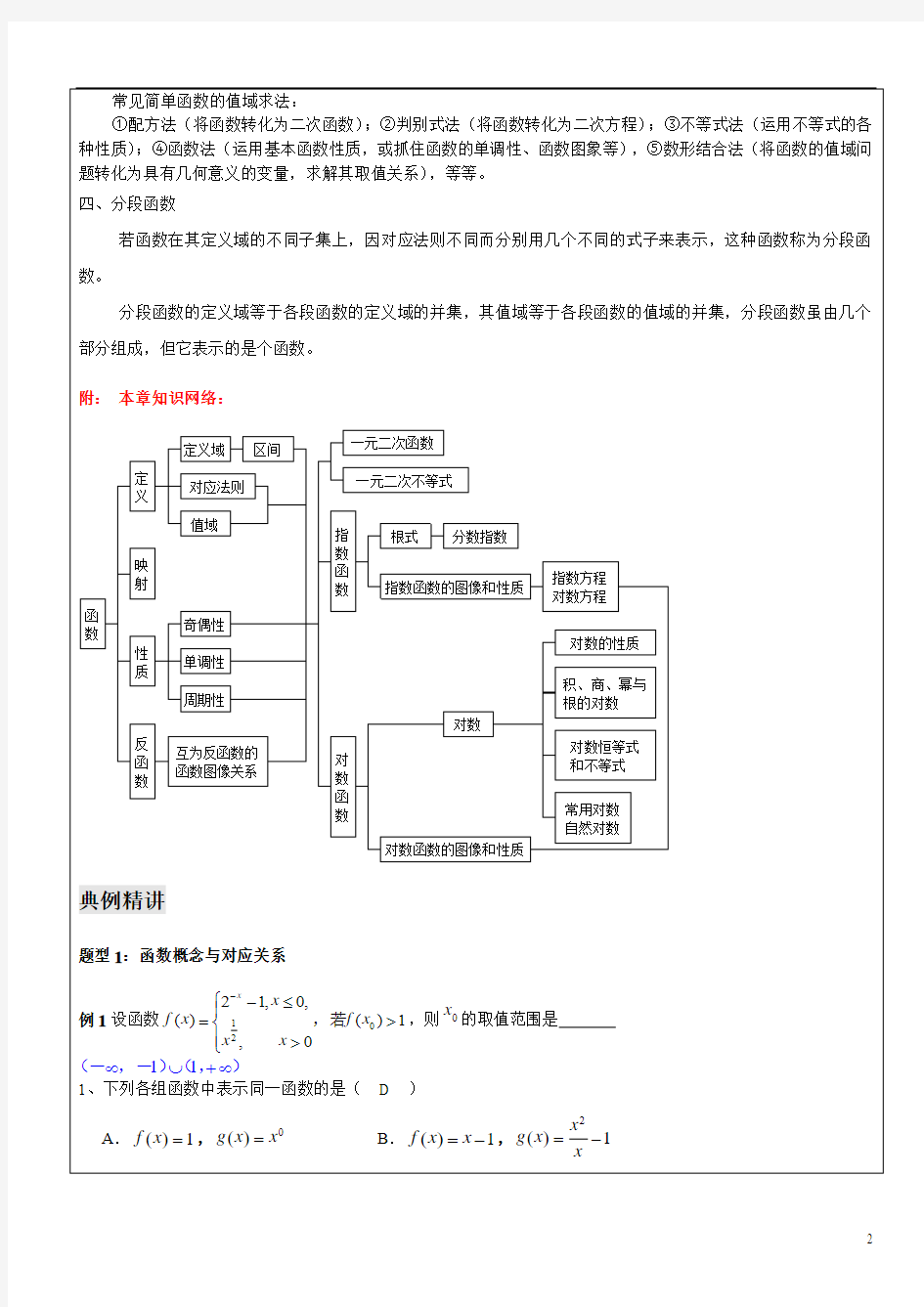
分段函数的定义域等于各段函数的定义域的并集，其值域等于各段函数的值域的并集，分段函数虽由几个部分组成，但它表示的是个函数。 附： 本章知识网络：

定

义

定义域

区间

对应法则值域

一元二次函数一元二次不等式

映射

函数

性质

奇偶性

单调性周期性

指数函数

根式分数指数

指数函数的图像和性质

指数方程对数方程

反函数

互为反函数的函数图像关系

对数函数

对数

对数的性质

积、商、幂与根的对数

对数恒等式和不等式常用对数自然对数对数函数的图像和性质

典例精讲

题型1：函数概念与对应关系

例1设函数1

0221,0,()()1,0x x f x f x x x -?-≤?

=>??>?，若，则0x 的取值范围是 11∞?+∞（－，－）（，）

1、下列各组函数中表示同一函数的是（ D ）

A ．()1f x =，0

()g x x = B ．()1f x x =-，2

()1x g x x

=-

C ．2()f x x =，4()()g x x =

D ．x x f =)(，3

3)(x x g =

2、下列函数中，与函数y x =相同的函数是 （ C ）

.A 2x y x

= .B 2()y x = .C lg10x

y = .D 2log 2x y = 例2 下列为函数y ＝)(x f 的图像的为（ D ）

巩固训练

1、下列各图形中，不可能是某函数)(x f y =的图象的是（ B ）

（A ） （B ） （C ） （D ）

2、向高为H 的水瓶中匀速注水，注满为止，如果注水量V 与水深h 的函数关系如图所示，那么水瓶形状是（ B ）

y

x

O

（A ）

y x

O

（B ）

y x

O

·

（C ）

y

x

O

-1 （D ）

O

x

y

x

y

O

x

y

O

x

y

O

H h V （A ） （B ） （C ） （D ）

例2若函数21()0

x f x π?+?

=???

)0()0()0(<=>x x x ，则(((2008)))f f f -=21π+ 类似这类问题一般都是周期性循环出现，在遇到这类问题是不要被题目表面的复杂性所迷惑，逐步去找出其中的

循环关系。 例3 设2

21

)(+=

x

x f ，利用课本中推导等差数列前n 项和的公式的方法，可求得 )6()5()0()4()5(f f f f f +++++-+- 的值为32 提示：11

1

1

2222()(1)2

222222

222222x x x x x x

x

f x f x -++-=

+

=

+

=

=

++++?+? 设(5)(4)(0)(5)(6)S f f f f f =-+-+++++ 则(6)(5)(0)(4)(5)S f f f f f =+++++-+-

∴ 2[(5)(6)][(4)(5)][(1)(0)][(6)(5)]63S f f f f f f f f =-++-+++++++-=

∴ 32S =．

巩固练习： 已知函数2

2

()1x f x x

=＋，那么111(1)(2)()(3)()(4)()234f f f f f f f ++++++＝____ 提示：()f x ＝2

2

1x x

＋，1()f x ＝211x ＋，()f x ＋1()1f x =． ∴ 111

(1)(2)()(3)()(4)()234f f f f f f f ++++++＝1711122

+++=．

这类求值问题一般变量都成对出现，或两两组合，或倒序相加，做题时要善于观察式子的特点，找到规律，同时

对具有这些运算性质的函数应逐步积累。

题型2：函数图象

例4 作出下列函数的图象：

(1)???---=14)(22x x x f )20()02(≤<≤≤-x x ； (2)322

-+=x x y ；01

()2(3)||x y x x

+=- 解：（1）函数图象如下：

（2）

2223(02)23(20)x x x x y x x x ?+-≥≤-?=?----<

(1)4(02)(1)2(20)x x x x x ?+-≥≤-?=?-+--<

或

函数的图象如右上．

（3）11

(0)22y x x x =-<≠-且，图象如右上．

常见的绝对值函数应掌握其画法，如()()f x f x 、等。

题型3：函数定义域

例5 函数y=)1(log 2

2

1-x 的定义域是( )

A.［-2,-1］∪(1,2)

B.(-3,-1)∪(1,2)

C.［-2,-1］∪(1,2)

D.(-2,-1)∪(1,2)

解析：22222212101111log (1)011222x x x x x x x x x ?->><-???>>????????????-≥-≤≤-≤≤????????或21x -≤<-或

12x <≤.∴212

log (1)y x =-的定义域为(

2,11,2???--????.

巩固练习：若12

1

()log (21)

f x x =

+，则)(x f 定义域为 （ A ）

A. )0,21(-

B. ]0,21(-

C. ),2

1

(+∞- D. )0(∞+，

例6 已知函数)(x f 的定义域为[]0,4，求函数)()3(2x f x f y ++=的定义域为

提示：由题意有2

034

04x x ≤+≤??≤≤?

解得 21x -≤≤，故此函数的定义域为[]2,1-．

巩固练习若函数()f x 的定义域为[]2,2-，则函数()f x 的定义域是

提示：()f x 中的x 相当于()f x 中的x ，则22x -≤≤，∴ 04x ≤≤，答案为[]0,4．

(())f g x 的定义域求法：若()f x 的定义域是[,]a b ，则()a g x b ≤≤，解出x 即(())f g x 的定义域。 1、若函数)(x f 的定义域为]2,1[-，则函数)1(-x f 的定义域为 2、若函数y ＝)13(-x f 的定义域是[1，2]，则y ＝)(x f 的定义域是____________ [2，5] 3、若函数)1(2

-x f 的定义域为]2,1[-，则函数)1(+x f 的定义域为

4、若函数3

44

)(2

++-=

mx mx x x f 的定义域为R ，则实数m 的取值范围是______ 5、已知函数)(x f ＝1

1

+x ，则函数)]([x f f 的定义域是（ D ） （A ）{x |x ≠1}；

（B ）{x |x ≠－2}； （C ）{x |x ≠1且x ≠－2}； （D ）{x |x ≠－1且x ≠－2}． 6、若函数()f x 的定义域是[2,4]-，求函数()()()F x f x f x =+-的定义域。

例7 函数＝268y kx x k =-++的定义域为R ，则k 的取值范围是 提示：∵2680kx x k -++≥恒成立， 0k ≤显然不符，

∴ 0364(8)0k k k >???+≤?

＝－， 解得：1k ≥．

定义域为R 要注意二次项系数为0的情况。 巩固练习：已知函数f （x ）=

3

1

32

3

-+-ax ax x 的定义域是R ，则实数a 的取值范围是（ ） A ．13

a >

B ．120a -<≤

C ．120a -<<

D ． 13

a ≤

解：由0a =或2

0,

4(3)0,

a a a ≠??

=-?-

题型3：函数值域与最值 例8 求下列函数的值域：

（1）2432y x x =-+-； （2）12y x x =+-；

（3）221

223x x y x x -+=-+； （4）35y x x =-+-；

（5）251

x

y x =+； （6）31--+=x x y ；

（7）x

x

y sin 2sin 2+-=

解：（1）24(1)4y x =---+，

∵ 2

0(1)44x ≤--+≤， ∴ 20(1)42x ≤--+≤ ∴224(1)44x ≤---+≤

∴所给函数的值域为[]2,4

（2）令12x t -=(0t ≥)，则x=2

12

t -．

∴ 2

12

t y t -=+21(1)12t =--+，当1t =时，max 1y =

∴所给函数的值域为(,1]-∞.

（3）由已知得：2(21)(21)(31)0y x y x y ---+-=…………（*）

①当210y -=时，12y =

，代入（*）式，不成立，∴12

y ≠． ②当210y -≠时，则：

211312231102(21)4(21)(31)010

2y y y y y y y ??≠?≠????≤

?=----≥??? ∴ 所给函数的值域为31

[,)102

．

（4）30

3550x x x -≥?≤≤?

-≥?

由得 ∴函数定义域为[]3,5

2222(3)(5)221(4)y x x x =+--=+-- 又

当4x =时，2max 4y =，当35x =或时，2min 2y = ∴ 224y ≤≤ 0y > ∴22y ≤≤ ∴ 所给[2,2]函数的值域为

（5）提示：y ＝

2255(51)x -+, ∵205(51)x ≠+, ∴2

5

y ≠ （6）函数13y x x =+-- 的值域是[4,4]-

提示：作出函数的图象，得值域为[4,4]-．

（7）由2sin 2sin x

y x

-=+解得：22sin 1y x y -=+，由|sin |1x ≤得22|

|11y y -≤+ 两边平方后整理，得：2

31030y y -+≤，解得：133

x ≤≤，

故所给函数的值域为1

[,3]3

．

常见的函数的值域的求法要掌握，如配方法、换元法、反解法、数形结合等。

巩固练习：

1、函数

2211x y x -=

+的值域为 提示：由2

211x y x

-=+得：2101y x y -=≥+，解得：11y -<≤． 2、函数24813

6(1)x x y x ++=

+ (1x >-)的值域是[2,)+∞ 提示：

24(1)923(1)26(1)32(1)

x y x x x ++==++≥++， 当且仅当1

23(1)32(1)

x x x >-??

?+=?+?

即12x =时取等号．又函数无最大值，故函数值域为[2,)+∞．

3、函数22

43

6

x x y x x ++=+-的值域是_________- 解：由已知得2

(1)(4)(63)0y x y x y -+--+= (*) ① 若1y =，代入（*）式390x --=，∴3x =-， 此时原函数分母26x x +-的值为0，∴1y ≠；

② 若1y ≠，则2(4)4(1)(63)0

1y y y y ??=-+-+≥?

≠?

2(52)01y y ?-≥??≠?1y ?≠ 但当25y =时，代入(*)得：3x =-，∴2

5

y ≠

∴函数的值域为：2

{|,1}5

y y R y y ∈≠≠且．

评注：本题中需要检验的原因是：函数2243

6

x x y x x ++=+-可化简为1(3)2x y x x +=

≠--．

例9已知函数2()3y f x x ax ==++在区间[]1,1-上的最小值为3-，求实数a 的值．

解：2

2()()324

a a y f x x ==++-

（1）min 12(1)432

a

a y f a -

<->=-=-=-当，即时，，解得：7a = （2）当112a -≤-≤，即22a -≤≤时，2

min ()3324a a y f =-=-=-，解得26a =±（舍去）

（3）当12

a

->，即2a <-时，min (1)43y f a ==+=-，解得：7a =-．

综合（1）（2）（3）可得：7a =±．

巩固练习：

已知函数12)(2++=ax x x f 在区间[1,2]-上的最大值为4，求a 的值．

解：22()()1y f x x a a ==++-

（1）当1

2

a -≤，即12a ≥-时，在2x =时函数有最大值，

(2)544f a =+=，解得1

4

a =-，适合；

（2）当12a ->，即1

2

a <-时，在1x =-时函数有最大值，

(1)224f a -=-=，解得1a =-，适合．

综上所述：1

4

a =-或1a =-．

二次函数的最值问题分类讨论是学生必备技能，必须过关。

题型4：函数解析式

例10 （1）若(1)=2f x x x ++,求()f x 。

（2）已知()f x 是一次函数，且满足3(1)2(1)217f x f x x +--=+，求()f x ；

（3）已知[]22

1)(,21)(x x x g f x x g -=-= (0x ≠)， 求)21(f ．

解：（1）解法一（换元法）：令1t x =

+则21,1x t t =-≥代入原式有

22()(1)2(1)1f t t t t =-+-=- ∴2()1(1)f x x x =-≥

解法二（定义法）：2

2(1)1x x x +=+- ∴2

(1)(1)1f x x +=+-

11x +≥ ∴2()1,(1)f x x x =-≥

（2）设()(0)f x ax b a =+≠，由3(1)2(1)217f x f x x +--=+得：

3[(1)]2[(1)]217a x b a x b x ++--+=+，∴ 5217ax a b x ++=+

∴ 2

517a a b =??+=?

，解得：27a b =??=?，∴ ()27f x x =+．

（3）令1()122g x x =-=，得14x =．∴ 2

211()14()15

12()

4

f -==．

函数解析式常用求法：待定系数法、换元法、配凑法、方程组法等，各有其使用范围，做题时加以体会。

题型5：分段函数与抽象函数

例11 已知函数22

4,0()4,0

x x x f x x x x ?+≥=?-

(2)(),f a f a ->则实数a 的取值范围是（ ） A (,1)(2,)-∞-?+∞ B (1,2)- C (2,1)- D (,2)(1,)-∞-?+∞ 解析：由已知，函数在整个定义遇上单调递增的。故2

(2)()f a f a -> ，等价于

220a a +-<，解得21a -<<

巩固练习：

若函数()f x =21

2

log ,0,log (),0x x x x >??

?-()f a -,则实数a 的取值范围是（ ）

（A ）()()1,00,1-? （B ）()(),11,-∞-?+∞ （C ）()()1,01,-?+∞） （D ）()(),10,1-∞-?

解析：当0a >时，由()()f a f a >-得：212

log log a a >，即22

1log log a a

>，即1

a a >，

解得1a >；当0a <时，由()()f a f a >-得：12

log ()a ->2()log a -，即21log ()a

->2()log a -，

即1

a

-

>a -，解得10a -<<，故选C 。 分段函数问题的解题方法是“分段解决”，各段解决完后，再综合.

例12 已知函数()f x 满足：1

(1)4

f =

，4()()()f x f y f x y =+ (),f x y +- (,)x y R ∈，则(2010)f =_______．

解析：取1,0x y ==得1(0)2

f =

法一：通过计算(2),(3),(4)........f f f ，寻得周期为6故()12010(0)2

f f ==

法二：取,1x n y ==,有()f n =(1)f n ++(1)f n -,同理(1)f n +=(2)f n ++()f n 联立得(2)f n += (1)f n -- 所以6T = 故()12010(0)2

f f ==.

巩固练习：

已知函数)(x f 是定义在实数集R 上的不恒为零的偶函数，且对任意实数x 都有 )()1()1(x f x x xf +=+，则

)2

5

(f 的值是( ) A. 0 B.

21 C. 1 D. 25 解析：若0x ≠，则有1(1)()x f x f x x

++=，取1

2x =-，则有：

111112()(1)()12222

f f f -

=-+=

-- 11()()22f f =--=-（∵()f x 是偶函数，则 11()()22f f -= ）由此得1()02f =于是，31533532()(1)()()3222322

f f f f +

=+=

= 1151511

2(1)[]()5()0132322

2

f f f +

=+=== 解决抽象函数问题，要全面地应用其所具有的性质展开解题思路.通常的方法是赋值法.要善于根据题目条件寻找符合条件的函数原型，帮助探求结论，找到解决问题的思路和方法.练习归纳了常见的函数原型，最好记住。

课后小练：

1、已知1)1(+=+x x f ，则=)(x f _________________

2、若函数)12(-x f ＝6x ＋1，则)1(f ＝_______7

3、已知3

311()f x x x

x

+=+

，则()f x )_________3

()3f x x x =-（2x ≥或2x ≤-） 4、函数4

)(,2)(2-=-=x x

x g x x f ，则)()()(x g x f x F ?=的解析式为=)(x F _____________

5、已知2()f x 的定义域为[1,1]-，则(2)x

f 的定义域为_____________ 6、若)(x f 是一次函数，14)]([-=x x f f 且，则)(x f = _______________

7、已知2

2

1111x x

x x f +-=??? ??+-，则)(x f 的解析式可取为 （ A ） （A ）21x x + （B ）212x x +- （C ）212x x + （D ）－2

1x

x

+ 8、已知函数()2

21364f x x x ??-=-+??

，求函数()1f x + 的解析式。

9、已知()f x 满足12()()3f x f x x

+=，求()f x 。 答案：2x x

-

10、已知函数()21f x x =-，2,0

()1,0

x x g x x ?≥=?-

答案：221(0)(())3(0)x x f g x x ?-≥=?-

1(21)()2

(())11()

2x x g f x x ?-≥??=??-

分段函数

1、设函数3,(10)

()((5)),(10)

x x f x f f x x -≥?=?

+

2、已知函数???=x x x f 2)( 11<≥x x ；???

??-=x

x

x g 1)( 11-<-≥x x ，则._______________)()(=+x g x f

3、已知1(0)()1(0)x f x x ≥?=?

-

，则不等式(2)(2)5x x f x +++≤的解集是___________3,2?

?-∞ ???

4、已知函数2

2,1(),122,2x x f x x x x x -+≤-??=-??≥?

＜＜，求满足()3f x =方程解。

5、已知函数)(x f ＝???<->+0

20132x x x x x ，　，，（1）求函数的定义域；（2）求)2(2

+a f 、)2(+a f ；

（3）若)(m f ＝10，求m ． 解：（1）定义域为：(－∞，0)∪(0，＋∞)；

（2）)2(2

+a f ＝32

a ＋7；

)2(+a f ＝?

??-<+->+222

732

a a a a a ，　，． （3）)(m f ＝???<->+020132m m m m m ，　，，∴???>=+01013m m 或???<=-0

10

22m m m ，

得：m ＝3或m ＝1－11．

1、下列哪组中的两个函数是同一函数（ B ）

（A ）2

()y x =与y x = （B ）3

3()y x =与y x =

（C ）2

y x =与2()y x = （D ）33

y x =与2

x y x

=

2、若函数)23(x f -的定义域为[]1,2-，则函数)(x f 的定义域是 （ C ）

.A ]1,25[-- .B []1,2- .C []1,5- .D ]2,2

1

[

3、已知函数(1)f x +的定义域为[]2,3-，则()21f x -的定义域 （ A ）

.A 50,2??

????

.B []1,4- .C []5,5- .D []3,7- 4、已知1)1(+=+x x f ，则函数)(x f 的解析式为 （ C ） （A ）2

)(x x f = （B ）)1(1)(2

≥+=x x x f （C ）)1(22)(2

≥+-=x x x x f （D ）)1(2)(2

≥-=x x x x f

5、函数)

34(log 1

)(2

2-+-=

x x x f 的定义域为 （ ）

.A ()()1,22,3 .B (,1)(3,)-∞+∞ .C ()1,3 .D []1,3

6、已知32)121(+=-x x f ，且 6)(=m f ，则m 等于 （ A ）

（A ） 41- （B ）41 （C ） 23 （D ）2

3

-

7、给出函数?????<+≥=)

4(),1()4(,

)21()(x x f x x f x

，则=)3(log 2f （ D ）

（A ）823- (B) 111 (C) 191 (D) 241 8、若22

1)1(x

x x x f +=-，则函数)1(-x f =__________223x x -+

9、已知f(x)是奇函数，g(x)是偶函数，且f(x)+g(x)= 11

-x ，则f(x)= ___21

x x -

10、函数)23(log )12(-=-x y x 的定义域为 2

{|1}3

x x x >≠且

11、若函数2743kx y kx kx +=

++的定义域为R ，则k ∈__________30,4??

????

12、设函数2

(1).(1)

()4 1.(1)

x x f x x x ?+

13、已知()f x 是一次函数，且满足3(1)2(1)217f x f x x +--=+，求()f x ； 解：设()(0)f x ax b a =+≠，

则3(1)2(1)333222f x f x ax a b ax a b +--=++-+-5217ax b a x =++=+， ∴2a =，7b =， ∴()27f x x =+。

14、已知1)(2

-=x x f ，1)(+=x x g ，求)]([x g f ]和)]([x f g 的解析式，并求其定义域。

15、设函数).89(,)100()]5([)100(3

)(f x x f f x x x f 求?

?

?<+≥-=

回顾总结

1、求函数定义域一般有三类问题：

（1）给出函数解析式的：函数的定义域是使解析式有意义的自变量的取值集合；

（2）实际问题：函数的定义域的求解除要考虑解析式有意义外，还应考虑使实际问题有意义； （3）已知()f x 的定义域求[()]f g x 的定义域或已知[()]f g x 的定义域求()f x 的定义域： ①掌握基本初等函数（尤其是分式函数、无理函数、对数函数、三角函数）的定义域； ②若已知()f x 的定义域[],a b ，其复合函数[]()f g x 的定义域应由()a g x b ≤≤解出。

2、求函数值域的各种方法

函数的值域是由其对应法则和定义域共同决定的。其类型依解析式的特点分可分三类：(1)求常见函数值域；(2)求由常见函数复合而成的函数的值域；(3)求由常见函数作某些“运算”而得函数的值域。

①直接法：利用常见函数的值域来求：

一次函数(0)y ax b a =+≠的定义域为R ，值域为R ； 反比例函数)0(≠=

k x

k

y 的定义域为{}0x x ≠，值域为{}0y y ≠； 二次函数)0()(2≠++=a c bx ax x f 的定义域为R ，

当0a >时，值域为2

(4){|}4ac b y y a -≥； 当0a <时，值域为2

(4){|}4ac b y y a

-≤。 ②配方法：转化为二次函数，利用二次函数的特征来求值；常转化为型如：),(,)(2

n m x c bx ax x f ∈++=的形式；

③分式转化法（或改为“分离常数法”）

④换元法：通过变量代换转化为能求值域的函数，化归思想；

⑤三角有界法：转化为只含正弦、余弦的函数，运用三角函数有界性来求值域；

⑥基本不等式法：转化成型如：)0(>+

=k x

k

x y ，利用平均值不等式公式来求值域； ⑦单调性法：函数为单调函数，可根据函数的单调性求值域。

⑧数形结合：根据函数的几何图形，利用数型结合的方法来求值域。

例如：① 形如212y x =

+，可采用 反解 法；②212

()323

x y x x +=≠-+，可采用 分离常数 法或 反解 法；③()()2

y a f x bf x c ????＝＋＋，可采用 配方 法；④1y x x =--，可采用 换

元 法；⑤2

1y x x =--，可采用 三角换元 法；⑥sin 2cos x

y x

=-可采用 数形结合、有界性

法等.3、求函数解析式的题型有：

（1）已知函数类型，求函数的解析式：待定系数法；

（2）已知()f x 求[()]f g x 或已知[()]f g x 求()f x ：换元法、配凑法； （3）已知函数图像，求函数解析式；

（4）()f x 满足某个等式，这个等式除()f x 外还有其他未知量，需构造另个等式：解方程组法； （5）应用题求函数解析式常用方法有待定系数法等。

函数定义域值域求法十一种

高中函数定义域和值域的求法总结 一、常规型 即给出函数的解析式的定义域求法，其解法是由解析式有意义列出关于自变量的不等式 或不等式组，解此不等式(或组)即得原函数的定义域。 解：要使函数有意义，则必须满足 x 2 2x 15 0 ① 11 或 x>5。 3且x 11} {x |x 5}。 1 例2求函数y ' 定义域。 *16 x 2 解：要使函数有意义，则必须满足 sinx 0 ① 16 x 2 0 ② 由①解得2k x 2k ，k Z ③ 由②解得 4x4 ④ 由③和④求公共部分，得 4 x 或 0 x 故函数的定义域为(4， ］ (0,］ 评注：③和④怎样求公共部分？你会吗？ 二、抽象函数型 抽象函数是指没有给出解析式的函数，不能常规方法求解，一般表示为已知一个抽象函 数的定义域求另一个抽象函数的解析式，一般有两种情况。 (1)已知f(x)的定义域，求f ［g(x)］的定义域。 (2)其解法是：已知f (x)的定义域是］a , b ］求f ［g(x)］的定义域是解a g(x) b , 即为所求的定义域。 例3已知f(x)的定义域为［—2, 2］,求f (x 2 3 x 3，故函数的定义域是｛x | x (2)已知f ［g(x)］的定义域，求f(x)的定义域。 其解法是：已知f ［g(x)］的定义域是］a ， b ］，求f(x)定义域的方法是：由 a x b ，求 g(x)的值域，即所求f(x)的定义域。 例4已知f(2x 1)的定义域为］1，2］，求f(x)的定义域。 解：因为 1 x 2,2 2x 4,3 2x 1 5。 即函数f(x)的定义域是｛x 13 x 5｝。 三、逆向型 即已知所给函数的定义域求解析式中参数的取值范围。特别是对于已知定义域为 R ,求 参数的范围问题通常是转化为恒成立问题来解决。 例5已知函数y . mx 2 6mx m 8的定义域为R 求实数m 的取值范围。 分析：函数的定义域为 R ,表明mx 2 6mx 8 m 0 ,使一切x € R 都成立，由x 2项 例1求函数y ,x 2 2x 15 |x 3| 8 的定义域。 |x 3| 8 0 ② 由①解得 x 3或x 5。 由②解得 x 5或x 11 解：令 2 x 2 1 2 ，得 1 x 2 3，即 0 x 2 3，因此0 | x | 3，从而 1)的定义域。 3}。 ③和④求交集得x 3且x 故所求函数的定义域为 ｛x |x

求函数的定义域和值域的方法

解：求函数的定义域的常用方法 函数的定义域是高考的必考内容，高考对函数的定义域常常是通过函数性质或函数的应用来考查的，具有隐蔽性，所以在研究函数问题时必须树立“函数的定义域优先”的观念。因此掌握函数的定义域的基本求解方法是十分重要的。下面通过例题来谈谈函数的定义域的常见题型和常用方法。 一，已知函数解析式求函数的定义域 如果只给出函数解析式（不注明定义域），其定义域是指使函数解析式有意义的自变量的取值范围（称为自然定义域），这时常通过解不等式或不等式组求得函数的定义域。主要依据是：（1）分式的分母不为零，（2）偶次根式的被开方数为非负数，（3）零次幂的底数不为零，（4）对数的真数大于零，（5）指数函数和对数函数的底数大于零且不等于1，（6）三角函数中的正切函数y=tanx ，｛x ︱x ∈R 且 x ≠2 k π π+ ， k ∈z ｝和余切函数y=cotx ，｛x ︱x ∈R 且 x ≠k π，k ∈z ｝等。 例题一 求下列函数的定义域： （1） y=2）0+㏒（x —2）x 2 （2） 解：（1）欲使函数有意义，须满足 2≠0 x —1≥0 x —2＞0 解得：x ＞2 且 x ≠3 ，x ≠5 x —2≠1 ∴ 函数的定义域为（2，3）∪（3，5）∪（5，+∞） x ≠0 （2） 由已知须满足 tanx ﹥0 解得： k π ﹤x ﹤2 k π π+ （k ∈z ） x ≠2 k π π+ -4﹤x ﹤4 16—x 2 ﹥0 ∴ 函数的定义域为（-π，2 π - ）∪（0， 2 π ）∪（π，4） 二，复合函数求定义域 求复合函数定义域应按从外向内逐层求解的方法。最外层的函数的定义域为次外层函数的值域，依次求，直到最内层函数定义域为止。多个复合函数的求和问题，是将每个复合函数定义域求出后取其交集。 例题二（1）已知函数f （x ）的定义域为〔-2，2〕，求函数y=f （x 2-1）的定义域。 （2）已知函数y=f （2x+4）的定义域为〔0，1〕，求函数f （x ）的定义域。 （3）已知函数f （x ）的定义域为〔-1，2〕，求函数y=f （x+1）—f （x 2-1）的定义域。 （4）已知函数y=f （tan2x ）的定义域为〔0， 8 π 〕，求函数f （x ）的定义域。 分析：（1）是已知f （x ）的定义域，求f 〔g （x ）〕的定义域。其解法是：已知f

高中数学必修一幂函数及其性质

幂函数及其性质专题 一、幂函数的定义 一般地，形如y x α=（x ∈R ）的函数称为幂孙函数，其中x 是自变量，α是常数.如 112 3 4 ,,y x y x y x - ===等都是幂函数，幂函数与指数函数，对数函数一样，都是基本初等函数. 二、函数的图像和性质 （1）y x = （2）12 y x = （3）2y x = （4）1y x -= （5）3y x = 用描点法在同一坐标系内画出以上五个函数图像，通过观察图像，可以看出： 3．幂函数性质 （1）所有的幂函数在（0，+∞）都有定义，并且图象都过点（1，1）； （2）x ＞0时，幂函数的图象都通过原点，并且在[0，+∞]上，是增函数 （3）α＜0时，幂函数的图象在区间（0，+∞）上是减函数. 三．两类基本函数的归纳比较： ① 定义 对数函数的定义：一般地，我们把函数log a y x =（a ＞0且a ≠1）叫做对数函数，其中x 是自变量，函数的定义域是（0，+∞）． 幂函数的定义：一般地，形如y x α=（x ∈R ）的函数称为幂孙函数，其中x 是自变量，α是常数. ②性质 对数函数的性质：定义域：（0，+∞）；值域：R ；

过点（1，0），即当x =1，y =0； 在（0，+∞）上是增函数；在（0，+∞）是上减函数 幂函数的性质：所有的幂函数在（0，+∞）都有定义， 图象都过点（1，1）x ＞0时，幂函数的图象都通过原点， 在[0，+∞]上，y x =、2y x =、3 y x =、1 2 y x =是增函数， 在（0，+∞）上， 1y x -=是减函数。 【例题选讲】 例1．已知函数()() 2 53 1m f x m m x --=--，当 m 为何值时，()f x ： （1）是幂函数；（2）是幂函数，且是()0,+∞上的增函数；（3）是正比例函数；（4）是反比例函数；（5）是二次函数； 简解：（1）2m =或1m =-（2）1m =-（3）45m =- （4）2 5 m =-（5）1m =- 变式训练：已知函数()()2 223 m m f x m m x --=+，当 m 为何值时，()f x 在第一象限内它的图像是上升曲 线。 简解：2 20230 m m m m ?+>??-->??解得：()(),13,m ∈-∞-+∞ 例2．比较大小： （1）1122 ,1.7 （2）33 ( 1.2),( 1.25)--（3）1125.25,5.26,5.26---（4）30.5 30.5,3,log 0.5 例3．已知幂函数223 m m y x --=（m Z ∈）的图象与x 轴、y 轴都无交点，且关于原点对称，求m 的值． 解：∵幂函数223 m m y x --=（m Z ∈）的图象与x 轴、y 轴都无交点， ∴2 230m m --≤，∴13m -≤≤； ∵m Z ∈，∴2 (23)m m Z --∈，又函数图象关于原点对称， ∴2 23m m --是奇数，∴0m =或2m =． 例4、设函数f （x ）＝x 3， （1）求它的反函数； （2）分别求出f － 1（x ）＝f （x ），f － 1（x ）＞f （x ），f － 1（x ）＜f （x ）的实数x 的范围． 解析：（1）由y ＝x 3两边同时开三次方得x ＝3y ，∴f － 1（x ）＝x 3 1 ． （2）∵函数f （x ）＝x 3和f －1 （x ）＝x 3 1 的图象都经过点（0，0）和（1，1）．

高中数学-函数定义域、值域求法总结

函数定义域、值域求法总结 一.求函数的定义域需要从这几个方面入手： （1）分母不为零 （2）偶次根式的被开方数非负。 （3）对数中的真数部分大于0。 （4）指数、对数的底数大于0，且不等于1 （5）y=tanx 中x ≠k π+π/2；y=cotx 中x ≠k π等等。 ( 6 )0x 中x 0≠ 二、值域是函数y=f(x)中y 的取值范围。 常用的求值域的方法： （1）直接法 （2）图象法（数形结合） （3）函数单调性法 （4）配方法 （5）换元法 （包括三角换元）（6）反函数法（逆求法） （7）分离常数法 （8）判别式法 （9）复合函数法 （10）不等式法 （11）平方法等等 这些解题思想与方法贯穿了高中数学的始终。 定义域的求法 1、直接定义域问题 例1 求下列函数的定义域： ① 2 1 )(-=x x f ；② 23)(+=x x f ；③ x x x f -+ +=211)( 解：①∵x-2=0，即x=2时，分式 2 1 -x 无意义， 而2≠x 时，分式 21 -x 有意义，∴这个函数的定义域是{}2|≠x x . ②∵3x+2<0，即x<-32 时，根式23+x 无意义， 而023≥+x ，即3 2 -≥x 时，根式23+x 才有意义， ∴这个函数的定义域是{x |3 2 -≥x }.

③∵当0201≠-≥+x x 且，即1-≥x 且2≠x 时，根式1+x 和分式x -21 同时有意义， ∴这个函数的定义域是{x |1-≥x 且2≠x } 另解：要使函数有意义，必须： ? ??≠-≥+0201x x ? ???≠-≥21 x x 例2 求下列函数的定义域： ①14)(2 --= x x f ②2 14 3)(2-+--= x x x x f ③= )(x f x 11111++ ④x x x x f -+= 0)1()( ⑤3 7 3132+++-=x x y 解：①要使函数有意义，必须：142 ≥-x 即： 33≤≤-x ∴函数14)(2--= x x f 的定义域为： [3,3-] ②要使函数有意义，必须：???≠-≠-≤≥?? ??≠-+≥--131 40210432x x x x x x x 且或 4133≥-≤<--

高一人教版必修一 数学函数定义域、值域、解析式题型

高一函数定义域、值域、解析式题型 一、 具体函数的定义域问题 1 求下列函数的定义域 （1 ）1 y = （2 ）y = （2）（3） 若函数()f x =的定义域为R ，则实数m 的取值范围是（ ） (A)04m <<(B) 04m ≤≤ (C) 4m ≥ (D) 04m <≤ 二、 抽象函数的定义问题 （一）已知函数()f x 的定义域，求函数[()]f g x 的定义域 2. 已知函数()f x 的定义域为[0,1]，求函数2(2)f x 的定义域。 （二）已知函数[()]f g x 的定义域，求函数()f x 的定义域 3. 已知函数(21)f x +的定义域为[1,2]，求函数()f x 的定义域。 （三）已知函数[()]f g x 的定义域，求函数[()]f h x 的定义域 4. 已知函数2(1)f x -的定义域为(2,5)，求函数1()f x 的定义域。 5.已知函数f x ()的定义域为 [1,1]-，且函数()()()F x f x m f x m =+--的定义域存在，求实数m 的取值范围。

（一） 配凑法 5 .已知22113(1)x f x x x ++=+，求()f x 的解析式。 （二） 换元法 6.已知(12f x +=+()f x 的解析式。 （三） 特殊值法 7 .已知对一切,x y R ∈，关系式()()(21)f x y f x x y y -=--+且(0)1f =，求()f x 。 待定系数法 8.已知()f x 是二次函数，且2(1)(1)244f x f x x x ++-=-+，求()f x 。 （四） 转化法 9. 设()f x 是定义在(,)-∞+∞上的函数，对一切x R ∈，均有()(2)0f x f x ++=，当11x -≤≤时，()21f x x =-，求当13x <≤时，函数()f x 的解析式。 （五） 消去法 11.已知函数()f x 21()()x f x x -=，求()f x （六） 分段求解法 12. 已知函数2,()21,()1,0x x o f x x g x x ?≥=-=?-

二次函数定义域与值域习题(强烈推荐)

高中数学专题训练二次函数与幂函数 一、选择题 1．“a＝1”是“函数f(x)＝x2－2ax＋3在区间[1，＋∞)上为增函数”的( ) A．充分不必要条件B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 2．一次函数y＝ax＋b与二次函数y＝ax2＋bx＋c在同一坐标系中的图象大致是( ) 3．函数y＝xα(x≥1)的图象如图所示，α满足条件( ) A．α<－1 B．－1<α<0 C．0<α<1 D．α>1 4．若函数f(x)＝ax2＋bx＋c满足f(4)＝f(1)，那么( ) A．f(2)>f(3) B．f(3)>f(2) C．f(3)＝f(2) D．f(3)与f(2)的大小关系不确定 5．已知函数y＝x2－2x＋3在闭区间[0，m]上有最大值3，最小值2，则m 的取值范围是( ) A．[1，＋∞) B．[0,2] C．[1,2] D．(－∞，2] 6．(2010·安徽卷)设abc＞0，二次函数f(x)＝ax2＋bx＋c的图象可能是( ) 7．已知f(x)＝ax2＋2ax＋4(0f(x2) B．f(x1)

D．f(x1)与f(x2)的大小不能确定 二、填空题 8．已知y＝(cos x－a)2－1，当cos x＝－1时y取最大值，当cos x＝a时，y取最小值，则a的范围是________． 9．抛物线y＝8x2－(m－1)x＋m－7的顶点在x轴上，则m＝________. 10．设函数f1(x)＝x 1 2 ，f2(x)＝x－1，f3(x)＝x2，则f1(f2(f3(2010)))＝ ________. 11．在函数f(x)＝ax2＋bx＋c中，若a，b，c成等比数列且f(0)＝－4，则f(x)有最________值(填“大”或“小”)，且该值为________． 12．已知幂函数f(x)＝x 1－α 3 在(－∞，0)上是增函数，在(0，＋∞)上是 减函数，那么最小的正整数a＝________. 13．方程x2－mx＋1＝0的两根为α，β，且α>0,1<β<2，则实数m的取值范围是________． 三、解答题 14．已知函数f(x)＝2 x －x m，且f(4)＝－ 7 2 . (1)求m的值； (2)判断f(x)在(0，＋∞)上的单调性，并给予证明． 15．已知对于任意实数x，二次函数f(x)＝x2－4ax＋2a＋12(a∈R)的值都是非负的，求函数g(a)＝(a＋1)(|a－1|＋2)的值域．

函数定义域和值域

1．函数的定义、定义域、值域 2．两个函数相等的条件 (1)定义域相同． (2)对应关系完全一致． 知识点二函数的表示及分段函数 1．函数的表示方法 函数的三种表示法：解析法、图象法、列表法． 2．分段函数 如果函数y＝f(x)，x∈A，根据自变量x在A中不同的取值范围，有着不同的对应关系，那么称这样的函数为分段函数．分段函数是一个函数，分段函数的定义域是各段定义域的并集，值域是各段值域的并集． 知识梳理 1.函数与映射的概念 函数映射 两个集合A，B 设A，B是两个 非空数集 设A，B是两个 非空集合 对应关系f：A→B 如果按照某种确定的对应关 系f，使对于集合A中的任意 一个数x，在集合B中都有唯 如果按某一个确定的对应关 系f，使对于集合A中的任意 一个元素x，在集合B中都有

求()x f 与()x g 的解析式。 1.(绍兴质检)函数f (x )＝log 2(x 2＋2x －3)的定义域是( ) A.[－3，1] B.(－3，1) C.(－∞，－3]∪[1，＋∞) D.(－∞，－3)∪(1，＋∞) 2.已知f (x )是一次函数，且f [f (x )]＝x ＋2，则f (x )＝( ) A.x ＋1 B.2x －1 C.－x ＋1 D.x ＋1或－x －1 3.(湖州一模)f (x )＝???? ????13x （x ≤0），log 3x （x >0），则f ???? ?? f ? ????19＝( ) A.－2 B.－3 C.9 D.－9 4.(全国Ⅱ卷)下列函数中，其定义域和值域分别与函数y ＝10lg x 的定义域和值域相同的是( ) A.y ＝x B.y ＝lg x C.y ＝2x D.y ＝ 1x 5.(铜陵一模)设P (x 0，y 0)是函数f (x )图象上任意一点，且y 20≥x 2 0，则f (x )的解析式可以是( ) A.f (x )＝x －1x B.f (x )＝e x －1 C.f (x )＝x ＋4 x D.f (x )＝tan x 6.下列图象中，不可能成为函数y ＝f (x )的图象的是( )

函数定义域值域求法(全十一种)

创作编号： GB8878185555334563BT9125XW 创作者： 凤呜大王* 高中函数定义域和值域的求法总结 一、常规型 即给出函数的解析式的定义域求法，其解法是由解析式有意义列出关于自变量的不等式或不等式组，解此不等式（或组）即得原函数的定义域。 例1 求函数8 |3x |15 x 2x y 2-+--= 的定义域。 解：要使函数有意义，则必须满足 ?? ?≠-+≥--②① 8|3x |015x 2x 2 由①解得 3x -≤或5x ≥。 ③ 由②解得 5x ≠或11x -≠ ④ ③和④求交集得3x -≤且11x -≠或x>5。 故所求函数的定义域为}5x |x {}11x 3x |x {>-≠-≤ 且。 例2 求函数2 x 161 x sin y -+=的定义域。 解：要使函数有意义，则必须满足 ???>-≥②①0 x 160 x sin 2 由①解得Z k k 2x k 2∈π+π≤≤π， ③ 由②解得4x 4<<- ④ 由③和④求公共部分，得 π≤<π-≤<-x 0x 4或 故函数的定义域为]0(]4(ππ--，， 评注：③和④怎样求公共部分？你会吗？ 二、抽象函数型 抽象函数是指没有给出解析式的函数，不能常规方法求解，一般表示为已知一个抽象函数的定义域求另一个抽象函数的解析式，一般有两种情况。 （1）已知)x (f 的定义域，求)]x (g [f 的定义域。 （2）其解法是：已知)x (f 的定义域是［a ，b ］求)]x (g [f 的定义域是解b )x (g a ≤≤，即为所求的定义域。 例3 已知)x (f 的定义域为［－2，2］，求)1x (f 2-的定义域。 解：令21x 22≤-≤-，得3x 12≤≤-，即3x 02≤≤，因此3|x |0≤≤，从而3x 3≤≤-，故函数的定义域是}3x 3|x {≤ ≤-。

函数定义域值域求法总结

、函数定义域、值域求法总结

————————————————————————————————作者：————————————————————————————————日期：

函数定义域、值域求法总结 1、函数的定义域是指自变量“x ”的取值集合。 2、在同一对应法则作用下，括号内整体的取值范围相同。 一般地，若已知 f(x)的定义域为[a,b]，求函数f[g(x)]的定义域时，由于分别在两个函数中的x 和g(x)受同一个对应法则的作用，从而范围相同。因此f[g(x)]的定义域即为满足条件a ≤g(x)≤b 的x 的取值范围。 一般地，若已知 f[g(x)]的定义域为[a,b]，求函数 f(x)的定义域时，由于x 和g(x) 受同一个对应法则的作用, 所以f(x)的定义域即为当a ≤x≤b 时，g(x)的取值范围。 定义域是X 的取值范围，g(x)和h(x)受同一个对应法则的影响，所以它们的范围相同。 ()的定义域 求的定义域已知练习)2(],9,3[log :313-x f x f 一、定义域是函数y=f(x)中的自变量x 的范围。 求函数的定义域需要从这几个方面入手： （1）分母不为零 ():f (x),f[g(x)]题型一已知的定义域求的定义域 ()():f g x ,f (x)????题型二已知的定义域求的定义域 ()[]():f g x ,f h(x)????题型三已知的定义域求的定义域()[]()[] )x (h f x f x g f →→

（2）偶次根式的被开方数非负。 （3）对数中的真数部分大于0。 （4）指数、对数的底数大于0，且不等于1 （5）y=tanx 中x ≠k π+π/2；y=cotx 中x ≠k π等等。 ( 6 )0x 中x 0≠ 二、值域是函数y=f(x)中y 的取值范围。 常用的求值域的方法： （1）直接法 （2）图象法（数形结合） （3）函数单调性法 （4）配方法 （5）换元法 （包括三角换元） （6）反函数法（逆求法） （7）分离常数法 （8）判别式法 （9）复合函数法 （10）不等式法 （11）平方法等等 这些解题思想与方法贯穿了高中数学的始终。 三、典例解析 1、定义域问题 例1 求下列函数的定义域： ① 21)(-= x x f ；② 23)(+=x x f ；③ x x x f -++=21 1)( 解：①∵x-2=0，即x=2时，分式2 1 -x 无意义， 而2≠x 时，分式21 -x 有意义，∴这个函数的定义域是{}2|≠x x . ②∵3x+2<0，即x<-32 时，根式23+x 无意义， 而023≥+x ，即3 2 -≥x 时，根式23+x 才有意义， ∴这个函数的定义域是{x |3 2 -≥x }. ③∵当0201≠-≥+x x 且，即1-≥x 且2≠x 时，根式1+x 和分式x -21 同时有意义， ∴这个函数的定义域是{x |1-≥x 且2≠x } 另解：要使函数有意义，必须： ???≠-≥+0201x x ? ???≠-≥2 1 x x 例2 求下列函数的定义域： ①14)(2 --= x x f ②214 3)(2-+--=x x x x f ③= )(x f x 11111++ ④x x x x f -+= 0)1()( ⑤3 7 3132+++-= x x y 解：①要使函数有意义，必须：142 ≥-x 即： 33≤≤-x ∴函数14)(2--= x x f 的定义域为： [3,3- ]

定义域和值域的求法

定义域和值域的求法 Final revision by standardization team on December 10, 2020.

函数定义域求法总结 一、定义域是函数y=f(x)中的自变量x 的范围。 （1）分母不为零 （2）偶次根式的被开方数非负。 （3）对数中的真数部分大于0。 （4）指数、对数的底数大于0，且不等于1 （5）y=tanx 中x ≠k π+π/2；y=cotx 中x ≠k π等等。 ( 6 )0x 中x 0≠ 二、抽象函数的定义域 1.已知)(x f 的定义域，求复合函数()][x g f 的定义域 由复合函数的定义我们可知，要构成复合函数，则内层函数的值域必须包含于外层函数的定义域之中，因此可得其方法为：若)(x f 的定义域为()b a x ,∈，求出)]([x g f 中b x g a <<)(的解x 的范围，即为)]([x g f 的定义域。 2.已知复合函数()][x g f 的定义域，求)(x f 的定义域 方法是：若()][x g f 的定义域为()b a x ,∈，则由b x a <<确定)(x g 的范围即为)(x f 的定义域。 3.已知复合函数[()]f g x 的定义域，求[()]f h x 的定义域 结合以上一、二两类定义域的求法，我们可以得到此类解法为：可先由()][x g f 定义域求得()x f 的定义域，再由()x f 的定义域求得()][x h f 的定义域。 4.已知()f x 的定义域，求四则运算型函数的定义域 若函数是由一些基本函数通过四则运算结合而成的，其定义域为各基本函数定义域的交集，即先求出各个函数的定义域，再求交集。 函数值域求法四种 在函数的三要素中，定义域和值域起决定作用，而值域是由定义域和对应法则共同确定。研究函数的值域，不但要重视对应法则的作用，而且还要特别重视定义域对值域的制约作用。确定函数的值域是研究函数不可缺少的重要一环。对于如何求函数的值域，是学生感到头痛的问题，它所涉及到的知识面广，方法灵活多样，在高考中经常出现，占有一定的地位，若方法运用适当，就能起到简化运算过程，避繁就简，事半功倍的作用。本次课就函数值域求法归纳如下，供参考。 1. 直接观察法 对于一些比较简单的函数，其值域可通过观察得到。

必修一 函数的定义域及值域

个性化学科优化学案 辅导科目 数学 就读年级 学生 教师 徐亚 课 题 函数的概念 授课时间 2015年11月28 备课时间 2015年11月25日 教 学 目 标 1、理解函数的概念，明确确定函数的三个要素，会用区间表示函数的定义域和值域；掌握求函数定义域的基本原则。 2、了解函数的三种表示方法，并能选择合适的方法表示函数。 重、难 考 点 求函数的值域问题时要明确两点，一是值域的概念，二是函数的定义域和对应关系是确定函数的依据。 教学容 鹰击长空—基础不丢 1．定义：设A 、B 是两个非空集合，如果按照某种对应关系f ，使对于集合A 中的 一个数x ，在集 合B 中 确定的数f(x)和它对应，那么就称:f A B →为集合A 到集合的一个 ，记作： 2．函数的三要素 、 、 3．函数的表示法：解析法（函数的主要表示法），列表法，图象法； 4. 同一函数： 相同，值域 ，对应法则 . 1．区间的概念和记号 在研究函数时,常常用到区间的概念，它是数学中常用的述语和符号. 设a,b ∈R ,且a

幂函数知识点及典型题

幂函数 知识点 一、幂函数的定义 一般地，形如y x α =（R x ∈）的函数称为幂孙函数，其中x 是自变量，α是常数.如1 12 3 4 ,,y x y x y x -===等 都是幂函数 二、幂函数的图像 幂函数n y x =随着n 的不同，定义域、值域都会发生变化，可以采取按性质和图像分类记忆的方法．熟练掌握n y x =，当11 2,1,,,323 n =±±± 的图像和性质，列表如下． ① 它们都过点()1,1，除原点外，任何幂函数图像与坐标轴都不相交，任何幂函数图像都不过第四象限． ② 11 ,,1,2,332a =时，幂函数图像过原点且在[)0,+∞上是增函数． ③ 1 ,1,22 a =---时，幂函数图像不过原点且在()0,+∞上是减函数． ④ 任何两个幂函数最多有三个公共点． 三、幂函数基本性质 （1）所有的幂函数在（0，+∞）都有定义，并且图象都过点（1，1）； （2）α＞0时，幂函数的图象都通过原点，并且在[0，+∞]上，是增函数 （3）α＜0时，幂函数的图象在区间（0，+∞）上是减函数. 四、解题方法总结 1．在研究幂函数的性质时，通常将分式指数幂化为根式形式，负整指数幂化为分式形式再去进行讨论； 2．对于幂函数y ＝α x ，我们首先应该分析函数的定义域、值域和奇偶性，由此确定图象的位置，即所在象 限，其次确定曲线的类型，即α＜0，0＜α＜1和α＞1三种情况下曲线的基本形状，还要注意α＝0，±1三个曲线的形状；对于幂函数在第一象限的图象的大致情况可以用口诀来记忆：“正抛负双，大竖小横”，即α＞0（α≠1）时图象是抛物线型；α＜0时图象是双曲线型；α＞1时图象是竖直抛物线型；0＜α＜1时图象是横卧抛物线型． 典型题 类型一、求函数解析式 例1.已知幂函数2 223 (1)m m y m m x --=--，当(0)x ∈+， ∞时为减函数，则幂函数y =__________． 类型二、比较幂函数值大小 例2.比较下列各组数的大小. (1)4 3 3.14 -与43 π - (2)35 (- 与35 (- (3）比较0.5 0.8 ，0.5 0.9，0.5 0.9 -的大小 类型三、求参数的范围

求函数的定义域与值域的常用方法完整版

求函数的定义域与值域 的常用方法 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】

求函数的定义域与值域的常用方法 引入： 自变量x 的取值范围为 定义域 因变量y 的取值范围为 值域 求函数的解析式、求函数的定义域、求函数的值域、求函数的最值? 一、求函数的解析式 （一）解析式的表达形式 （解析式的表达形式有一般式、分段式、复合式等。） 1、一般式 （是大部分函数的表达形式） 例：一次函数：b kx y +=)0(≠k 二次函数：c bx ax y ++=2 )0(≠a 反比例函数：x k y = )0(≠k 正比例函数：kx y = )0(≠k 2、复合式 若y 是u 的函数，u 又是x 的函数，即),(),(),(b a x x g u u f y ∈==，那么y 关于x 的函数[]()b a x x g f y ,,)(∈=叫做f 和g 的复合函数。 例1、已知3)(,12)(2+=+=x x g x x f ，则[]=)(x g f ， []=)(x f g 。 解：[]721)3(21)(2)(22+=++=+=x x x g x g f （二）解析式的求法 （根据已知条件求函数的解析式，常用配凑法、换元法、待定系数法、赋值（式）法、方程法等。） 1. 配凑法 例1.已知 ：23)1(2+-=+x x x f ，求f(x)； 解：因为15)1(23)1(22+-+=+-=+x x x x x f 例2、已知：221)1(x x x x f +=+，求)(x f 。 解： 2)1(1)1(222-+=+=+x x x x x x f ∴ )22(2)(2-≤≥-=x x x x f 或 注意：使用配凑法也要注意自变量的范围限制。 2.换元法 例1.已知：x x x f 2)1(+=+，求f(x); 解：令2)1(,1,1-=≥=+t x t t x 即则 则1)1(2)1()(22-=-+-=t t t t f 所以)1(1)(2≥-=x x x f 例2、已知：11)11(2-=+x x f ，求)(x f 。

数学必修一定义域值域知识点总结

数学必修一定义域值域知识点总结 数学必修一定义域知识点 定义 (高中函数定义)设A，B是两个非空的数集，如果按某个确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f(x)和它对应，那么就称f：A--B为集合A到集合B的一个函数，记作y=f(x)，x属于集合A。其中，x叫作自变量，x的取值范围A叫作函数的定义域; 常见题型 1，已知f(x)的定义域，求f(g(x))的定义域. 例1，已知f(x)的定义域为(-1，1)，求f(2x-1)的定义域. 略解：由-1<2x-1<1有0<1 ∴f(2x-1)的定义域为(0，1) 2，已知f(g(x))的定义域，求f(x)的定义域. 例2，已知f(2x-1)的定义域为(0，1)，求f(x)的定义域。 解：已知0<1，设t=2x-1 ∴x=(t+1)/2 ∴0<(t+1)/2<1 ∴-1<1 ∴f(x)的定义域为(-1,1) 注意比较例1与例2，加深理解定义域为x的取值范围的含义。 3，已知f(g(x))的定义域，求f(h(x))的定义域.

例3，已知f(2x-1)的定义域为(0，1)，求f(x-1)的定义域。 略解：如例2，先求出f(x)的定义域为(-1，1)，然后如例1有-1<1，即0<2 ∴f(x-1)的定义域为(0，2) 指使函数有意义的一切实数所组成的集合。 其主要根据： ①分式的分母不能为零 ②偶次方根的被开方数不小于零 ③对数函数的真数必须大于零 ④指数函数和对数函数的底数必须大于零且不等于1 例4，已知f(x)=1/x+√(x+1)，求f(x)的定义域。 略解：x≠0且x+1≧0， ∴f(x)的定义域为[-1，0)∪(0，+∞) 注意：答案一般用区间表示。 例5，已知f(x)=lg(-x2+x+2)，求f(x)的定义域。 略解：由-x2+x+2>0有x2-x-2<0 即-1<2 ∴f(x)的定义域为(-1，2) 函数应用题的函数的定义域要根据实际情况求解。 例6，某工厂统计资料显示，产品次品率p与日产量 x(件)(x∈N,1≦x<99)的关系符合如下规律： 又知每生产一件正品盈利100元，每生产一件次品损失100元. 求该厂日盈利额T(元)关于日产量x(件)的函数;

5、函数的定义域和值域答案

函数定义 映射 一般地，设A 、B 是两个非空的集合，如果按某一个确定的对应法则f ，使对于集合A 中的任意一个元素x ，在集合B 中都有唯一确定的元素y 与之对应，那么就称对应:f A B →为从集合A 到集合B 的一个映射（mapping ）．记作“:f A B →” 函数的概念 1．定义：如果A ，B 是非空的数集，如果按某个确定的对应关系f ，使对于集合A 中的任意一个数，在集合B 中都有唯一确定的数)(x f 和它对应，那么就称B A f →:为从集合A 到集合B 的一个函数，记作 )(x f y =，A x ∈。 其中，x 叫做自变量，x 的取值范围A 叫做函数的定义域；与x 的值相对应的y 的值叫做函数值，函数值的集合{}A x x f ∈|)(叫做函数的值域。 函数与映射的关系与区别 相同点:(1)函数与映射都是两个非空集合中元素的对应关系; (2)函数与映射的对应都具有方向性; (3)A 中元素具有任意性，B 中元素具有唯一性； 区别：函数是一种特殊的映射，它要求两个集合中的元素必须是数，而映射中两个集合的元素是任意的数学对象。 函数的三要素 函数是由三件事构成的一个整体，分别称为定义域．值域和对应法则．当我们认识一个函数时，应从这三方面去了解认识它． 例 函数y ＝x x 2 3与y ＝3x 是不是同一个函数？为什么？ 练习 判断下列函数f （x ）与g （x ）是否表示同一个函数，说明理由？ ① f ( x ) = (x －1) 0；g ( x ) = 1 ② f ( x ) = x ； g ( x ) = 2x ③ f ( x ) = x 2；f ( x ) = (x + 1) 2 ④ f ( x ) = | x | ；g ( x ) = 2x 重点一：函数的定义域各种类型例题分析

高中数学：幂函数的概念、图象和性质

高中数学：幂函数的概念、图象和性质 1、幂函数的概念 一般地，函数叫做幂函数，其中是自变量，是常数；其定义域是使有意义的值的集合。 例1、已知幂函数，且当时为减函数。求幂函数的解析式。 分析：正确理解幂函数的概念、幂函数的图象与性质。求幂函数的解析式，一般用待定系数法，弄明白幂函数的定义是解题的关键。 解答：由于为幂函数， 所以，解得，或。 当时，，在上为减函数； 当时，，在上为常函数，不合题意，舍去。 故所求幂函数的解析式为。 2、幂函数的图象和性质 图象： 定

义域值域奇 偶性奇偶奇 非奇非 偶 奇 单 调性上增 上减， 上增 上增上增 ， 上分别减 定 点 ， （1）所有的幂函数在上都有定义，并且图象都过点； （2）如果，则幂函数的图象过点和，并且在区间上是增函数； （3）如果，则幂函数的图象过点，并在区间上是减函数。在第一象限内，当从趋向于原点时，图象在轴右方无限地逼近轴，当趋于时，图象在轴上方无限地逼近轴； （4）当为奇数时，幂函数为奇函数；当为偶数时，幂函数为偶函数。 例2、比较，，的大小。 分析：先利用幂函数的增减性比较与的大小，再根据幂函数的图象比较与的大小。 解答： 而在上单调递增，且， 。故。

例3、若函数在区间上是递减函数，求实数m的取值范围。 分析：本题考查简单幂函数的性质以及函数图象的平移问题。 函数是一个比较常用的幂函数，它也叫做反比例函数，其定义域是，是一个奇函数，对称中心为（0，0），在和 上都是递减函数。一般地，形如的函数都可以通过对 的图象进行变换而得到，所以这些函数的性质都可以借助的性质来得到。 解答：由于，所以函数的图象是由幂 函数的图象先向右平移2个单位，再向上平移3个单位得到的，所以其图象如图所示。 其单调递减区间是和，而函数在区间上是递减函数，所以应有。 例4、若点在幂函数的图象上，点在幂函数的图象 上，定义，试求函数的最大值及其单调区间。分析：首先根据幂函数的定义求出，然后在同一坐标系下画出函数和的图象，得出的函数图象，最后根据图象求出最大值和单调区间。

求解函数定义域,值域,解析式讲义(精华版)

求解函数定义域、值域、解析式 【课堂笔记】 知识点一 定义域、值域的定义 在函数)(x f y =中，x 叫做自变量，x 的取值范围的集合A 叫作函数的定义域；与x 的值相对应的值y 叫作函数值，函数值的集合})({A x x f ∈叫作函数的值域。 下面我们就以求简单函数的定义域做一讲解。 （1）当函数是以解析式的形式给出的时候，其定义域是使函数解析式有意义的自变量的取值的集合。 （2）当函数是由实际问题给出时，其定义域不仅要考虑使其解析式有意义，还要有实际意义。 注意：（1）求函数的定义域，一般是转化为解不等式或不等式组的问题，要注意逻辑连接词的恰当使用。 （2）定义域是一个集合，其结果可用集合或区间来表示。 （3）若函数)(x f 是整式型函数，则定义域为全体实数。 （4）若函数)(x f 是分式型函数，则定义域为使分母不为零的实数构成的集合。 （5）若函数)(x f 是偶次根式，则定义域为使被开方式非负的实数构成的集合。 （6）由实际问题确定的函数，其定义域由自变量的实际意义确定。 （7）如果已知函数是由两个以上的数学式子的和、差、积、商的形式构成时，定义域是使其各部分有 意义的公共部分的集合。 （8）复合函数的定义域问题： ①若已知)(x f 的定义域为],[b a ,则复合函数))((x g f 的定义域可由不等式b x g a ≤≤)(解出； ②若已知))((x g f 的定义域为],[b a ，则函数)(x f 的定义域，即为当],[b a x ∈时函数)(x g 的值域。 【例1】求下列函数的定义域 （1）1+= x y （2）x y -= 21 （3）0)1(21-+-= x x y 【例2】 求下列函数的定义域 （1）x y ++ = 11 11； （2）1 42 --= x x y ；

数学定义域和值域

函数的有关概念 1．函数的概念：设A、B是非空的数集，如果按照某个确定的对应关系f，使对于集合A 中的任意一个数x，在集合B中都有唯一确定的数f(x)和它对应，那么就称f：A→B为从集合A到集合B的一个函数．记作：y=f(x)，x∈A．其中，x叫做自变量，x的取值范围A 叫做函数的定义域；与x的值相对应的y值叫做函数值，函数值的集合{f(x)| x∈A }叫做函数的值域． 经典例题透析 类型一、函数概念 1.下列各组函数是否表示同一个函数？ (1) (2) (3) (4) 小结1:相同函数的判断方法：①表达式相同（与表示自变量和函数值的字母无关）；②定义域一致(两点必须同时具备) 2.求下列函数的定义域(用区间表示). (1)；(2)；(3). 求函数的定义域时列不等式组的主要依据是： (1)分式的分母不等于零； (2)偶次方根的被开方数不小于零； (3)对数式的真数必须大于零； (4)指数、对数式的底必须大于零且不等于1. (5)如果函数是由一些基本函数通过四则运算结合而成的.那么，它的定义域是使各部分都有意义的x的值组成的集合. (6)指数为零底不可以等于零， (7)实际问题中的函数的定义域还要保证实际问题有意义. 3．值域: （先考虑其定义域） 实际上求函数的值域是个比较复杂的问题，虽然给定了函数的定义域及其对应法则以后，值域就完全确定了，但求值域还是特别要注意讲究方法，常用的方法有： 1.直接法:由常见函数的值域或不等式性质求出； 2.分离常数法：可将其分离出一个常数； 3.观察法：利用函数的图象的"最高点"和"最低点"，观察求得函数的值域；

4.判别式法：将函数视为关于自变量的二次方程，利用判别式求函数值的范围，常用于一些"分式"函数等；此外，使用此方法要特别注意自变量的取值范围； 5.换元法：通过对函数的解析式进行适当换元，将复杂的函数化归为几个简单的函数，从而利用基本函数的取值范围来求函数的值域. 例题详见备课本 5. 换元法 通过简单的换元把一个函数变为简单函数，其题型特征是函数解析式含有根式或三角函数公式模型，换元法是数学方法中几种最主要方法之一，在求函数的值域中同样发挥作用。 ∵0e x > ∴01y 1y >-+ 解得：1y 1<<- 故所求函数的值域为)1,1(- 例3. 求函数1x x y -+=的值域。 解：令t 1x =-，)0t (≥ 则1t x 2+= ∵ 43)21t (1t t y 22++=++= 又0t ≥，由二次函数的性质可知 当0t =时，1y m i n = 当0t →时，+∞→y 故函数的值域为),1[+∞