两个正态总体均值差的区间估计

两个正态总体均值差的区间估计

实验一

一、实验目的

熟悉SPSS的参数估计功能，熟练掌握两个正态总体均值之差（独立样本）的区间估计方法及操作过程，对SPSS运行结果能进行解释。

二、实验内容

【例】（数据文件为data03-1.sav）为估计两种方法组装产品所需要时间的差异，分别对两种不同的组装方法个随机安排12个工人，每个工人组装一件产品所需的时间（分钟）。数据如表1所示：

表1 两种方法组装产品所需的时间

试以95%的置信水平确定两种方法组装产品所需时间差值的置信区间。

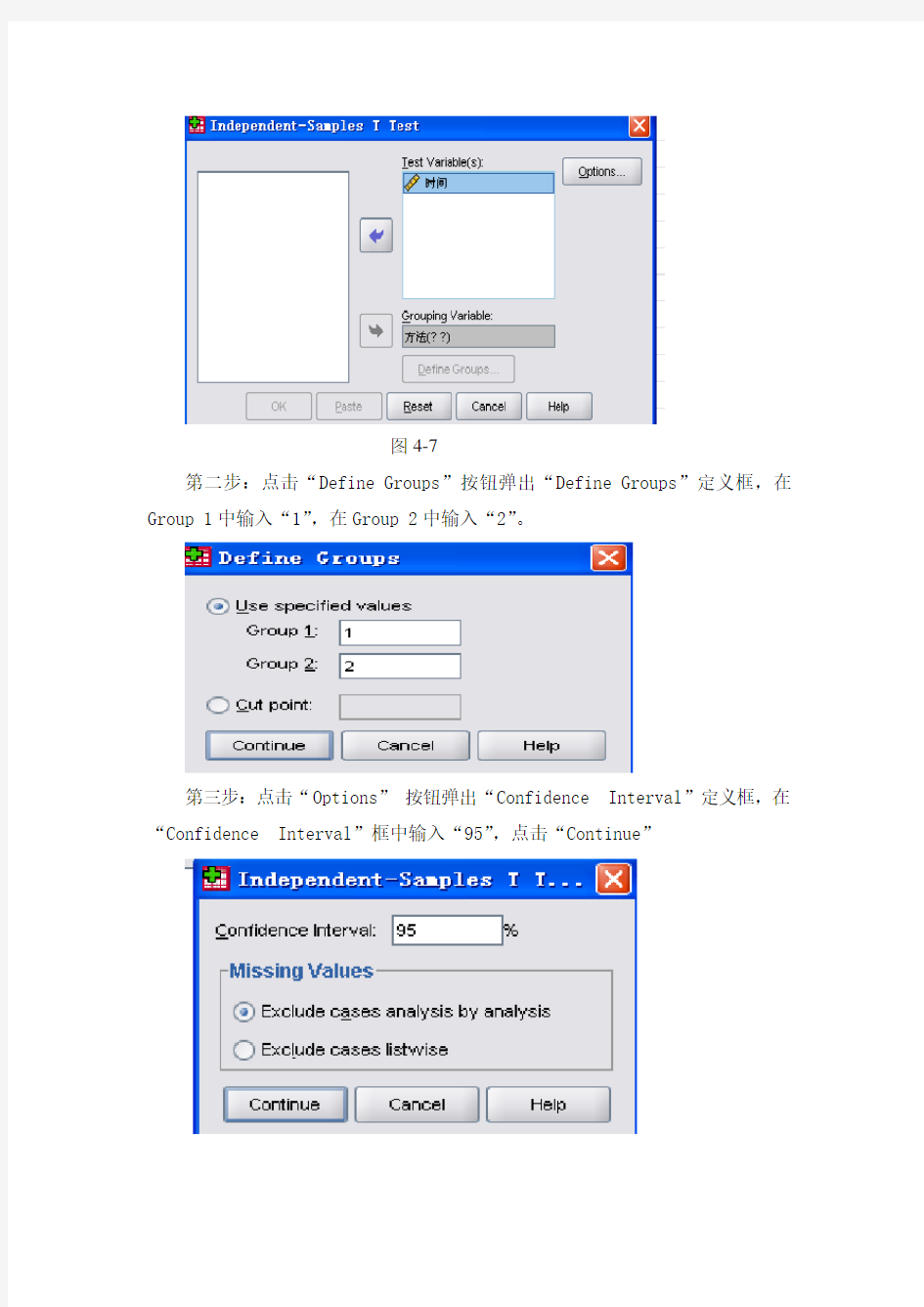
解：第一步，打开数据文件“data03-1.sav”，选择菜单“Analyze→Compare Means→Independent-samples T Test”项，弹出“Independent- samples T Test”对话框。从对话框左侧的变量列表中选“时间”，进入“Test Variable(s)”框，选择变量“方法”，进入“Grouping Variable”框。如图4-7所示

图4-7

第二步：点击“Define Groups”按钮弹出“Define Groups”定义框，在Group 1中输入“1”，在Group 2中输入“2”。

第三步：点击“Options”按钮弹出“Confidence Interval”定义框，在“Confidence Interval”框中输入“95”，点击“Continue”

第四步：单击“OK”按钮，得到输出结果。

输出结果表明：（假定两种方法组装产品的时间服从正态分布，且方差相等，两种方法组装产品所需时间差值的置信区间为[0.1403，7.2597]；假定两个总体的方差不相等，两种方法组装产品所需时间差值的置信区间为[0.1384，

7.2616]。）本例方差齐性检验结果：0.9170.05

=>=，不能拒绝原假设，同

pα

方差假定是合理的，因而，两种方法组装产品所需时间差值的置信区间为

（0.1403，7.2597）。

实验二：

一、实验目的

熟悉SPSS的参数估计功能，熟练掌握两个正态总体均值之差（匹配样本）的区间估计方法及操作过程，对SPSS运行结果能进行解释。

二、实验内容

【例】（数据文件为data03-2.sav）由10名学生组成一个随机样本，让他们分别采用A和B两套试卷进行测试。结果如表2所示：

表2 10名学生两套试卷的得分

试建立两套试卷平均分数之差在95%的置信区间。

解：第一步，打开数据文件data03-2.sav，选择菜单“Analyz e→Compare Means→Paired-samples T Test”项，弹出“Paired - samples T Test”对话框。从对话框左侧的变量列表中选择变量A卷、B卷进入Variables框。

第二步：点击“Options”按钮弹出“Confidence Interval”定义框，在“Confidence Interval”框中输入“95”，点击“Continue”

第三步：单击“OK”按钮，得到输出结果。

输出结果表明：两种试卷所产生的分数之差在95%的置信区间为（6.327，15.673）。

第四节正态总体的置信区间

第四节 正态总体的置信区间 与其他总体相比, 正态总体参数的置信区间是最完善的,应用也最广泛。在构造正态总体参数的置信区间的过程中，t 分布、2χ分布、F 分布以及标准正态分布)1,0(N 扮演了重要角色. 本节介绍正态总体的置信区间,讨论下列情形: 1. 单正态总体均值(方差已知)的置信区间; 2. 单正态总体均值(方差未知)的置信区间; 3. 单正态总体方差的置信区间; 4. 双正态总体均值差(方差已知)的置信区间; 5. 双正态总体均值差(方差未知但相等)的置信区间; 6. 双正态总体方差比的置信区间. 注: 由于正态分布具有对称性, 利用双侧分位数来计算未知参数的置信度为α-1的置信区间, 其区间长度在所有这类区间中是最短的. 分布图示 ★ 引言 ★ 单正态总体均值（方差已知）的置信区间 ★ 例1 ★ 例2 ★ 单正态总体均值（方差未知）的置信区间 ★ 例3 ★ 例4 ★ 单正态总体方差的置信区间 ★ 例5 ★ 双正态总体均值差（方差已知）的置信区间 ★ 例6 ★ 双正态总体均值差（方差未知）的置信区间 ★ 例7 ★ 例8 ★ 双正态总体方差比的置信区间 ★ 例9 ★ 内容小结 ★ 课堂练习 ★ 习题6-4 内容要点 一、单正态总体均值的置信区间(1) 设总体),,(~2σμN X 其中2σ已知, 而μ为未知参数, n X X X ,,,21 是取自总体X 的一个样本. 对给定的置信水平α-1, 由上节例1已经得到μ的置信区间 ,,2/2/???? ? ??+?-n u X n u X σσαα 二、单正态总体均值的置信区间(2) 设总体),,(~2σμN X 其中μ,2σ未知, n X X X ,,,21 是取自总体X 的一个样本. 此时可用2σ的无偏估计2S 代替2σ, 构造统计量 n S X T /μ-=, 从第五章第三节的定理知).1(~/--= n t n S X T μ 对给定的置信水平α-1, 由 αμαα-=? ?????-<-<--1)1(/)1(2/2/n t n S X n t P ,

第十九讲正态总体均值及方差的区间估计

第十九讲 正态总体均值及方差的 区间估计 1. 单个正态总体方差的区间估计 设总体),(~2σμN X ， ),,(21n X X X 为来自X 的一个样本，已给定置信度（水平）为α-1，求2σ的置信区间。 ①当μ已知时，由于),(~2σμN X i ，因此， )1,0(~N X i σ μ -（,2,1=i n , ）。 由2χ分布的定义知： ∑ =-n i i n X 1 22 2 )(~)(χσ μ， 据)(2n χ分布上α分位点的定义，有： αχσμχαα-=<-<∑ =-1)}()()({2 1 2 2 212 2 n X n P n i i 从而 αχμσχμαα-=????? ??-<

正态分布可信区间

3. 某地200例正常成人血铅含量的频数分布如下表。 （1）简述该资料的分布特征。 （2）若资料近似呈对数正态分布，试分别用百分位数法和正态分布法估计该地正常成人血铅值的95%参考值范围。 表某地200例正常成人血铅含量(μmol/L)的频数分布 血铅含量频数累积频数 0.00～7 7 0.24～49 56 0.48～45 101 0.72～32 133 0.96～28 161 1.20～13 174 1.44～14 188 1.68～ 4 192 1.92～ 4 196 2.16～ 1 197 2.40～ 2 199 2.64～ 1 200 [参考答案] （1）从表可以看出，血铅含量较低组段的频数明显高于较高组段，分布不对称。同正态分布相比，其分布高峰向血铅含量较低方向偏移，长尾向血铅含量较高组段延伸，数据为正偏态分布。 某地200例正常成人血铅含量(μmol/L)的频数分布 血铅含量组中值频数累积频数累积频率 0.00～0.12 7 7 3.5 0.24～0.36 49 56 28.0 0.48～0.60 45 101 50.5 0.72～0.84 32 133 66.5 0.96～ 1.08 28 161 80.5

1.20～ 1.32 13 174 87.0 1.44～ 1.56 14 188 94.0 1.68～ 1.80 4 192 96.0 1.92～ 2.04 4 196 98.0 2.16～ 2.28 1 197 98.5 2.40～ 2.52 2 199 99.5 2.64～ 2.76 1 200 100 （2）因为正常人血铅含量越低越好，所以应计算单侧95%参考值范围。 百分位数法：第95%百分位数位于1.68～组段，组距为0.24，频数为4，该组段以前的累积频数为188，故 95 (2000.95188) 1.680.24 1.80(μmol/L) 4 P ?- =+?= 即该地正常成人血铅值的95%参考值范围为小于1.80μmol/L。 正态分布法：将组中值进行log变换，根据题中表格，得到均值和标准差计算表。 某地200例正常成人血铅含量(μmol/L)均值和标准差计算表 血铅含量组中值lg组中值(x) 频数(f) fx2fx 0.00～0.12 -0.92 7 -6.44 5.9248 0.24～0.36 -0.44 49 -21.56 9.4864 0.48～0.60 -0.22 45 -9.9 2.178 0.72～0.84 -0.08 32 -2.56 0.2048 0.96～ 1.08 0.03 28 0.84 0.0252 1.20～ 1.32 0.12 13 1.56 0.1872 1.44～ 1.56 0.19 14 2.66 0.5054 1.68～ 1.80 0.26 4 1.04 0.2704 1.92～ 2.04 0.31 4 1.24 0.3844 2.16～ 2.28 0.36 1 0.36 0.1296 2.40～ 2.52 0.40 2 0.80 0.3200 2.64～ 2.76 0.44 1 0.44 0.1936 合计——200 -31.52 19.8098

正态总体均值及方差的假设检验表

正态总体均值及方差的假设检验表： 单正态总体均值及方差的假设检验表(显著性水平α) 1 a n ～N (0,1)2 01 a S n ～t 2 2 02 1 0n i n i a ～ 2或 2 21 2 n 2 2n 2 21 n 20 ～ 22 21 1 2 n 2 21n 21 1 n

2 212 12 n n ～N (0,1) 2 1 2 11W S n n ～ 2 , 22 1122 122 n S n S n n 22 22 21112 2 1 2 1i i n i i a a n ～12,F n n 2 或 2 2 221 n S n ～21,1n 1 2或 2

Z =ξ-η～N (a 1-a 2，21σ+2 2σ)，Z i =ξi -ηi . 2 21 2 Z n ) 2 1 S n ～ 2

单正态总体均值及方差的区间估计(置信度1-α) 已知 1 a n ～N (0,1)0 1 1 , n n u u n n 1 a S n ～t , 1 1 t t n n 2 02 1 n i n i a ～ 001 122, 12 2 i i i i n n a a 20 ～ 21 ,12 2 n

2个正态总体均值差及方差比的区间估计(置信度1-α) 12 212 12 a n n ～N (0,1) 2212 12 u n n 112 11W a S n n 22 n t 1 22 12 11W n n t S n n )2 a ξ-12 ,1 ,2 2 n n A F A 2 112 222 2 11n S n S ～ 2 2 21112W n S n S n n 212 1212 2 2 1 n i i n i i n a A n a ，2 122 2 21111n n S B n n S ． （注：专业文档是经验性极强的领域，无法思考和涵盖全面，素材和资料部分来自网络，供参考。可复制、编制，期待你的好评与关注）

两个正态总体均值差的区间估计

两个正态总体均值差的区间估计 实验一 一、实验目的 熟悉SPSS的参数估计功能，熟练掌握两个正态总体均值之差（独立样本）的区间估计方法及操作过程，对SPSS运行结果能进行解释。 二、实验内容 【例】（数据文件为data03-1.sav）为估计两种方法组装产品所需要时间的差异，分别对两种不同的组装方法个随机安排12个工人，每个工人组装一件产品所需的时间（分钟）。数据如表1所示： 表1 两种方法组装产品所需的时间 试以95%的置信水平确定两种方法组装产品所需时间差值的置信区间。 解：第一步，打开数据文件“data03-1.sav”，选择菜单“Analyze→Compare Means→Independent-samples T Test”项，弹出“Independent- samples T Test”对话框。从对话框左侧的变量列表中选“时间”，进入“Test Variable(s)”框，选择变量“方法”，进入“Grouping Variable”框。如图4-7所示

图4-7 第二步：点击“Define Groups”按钮弹出“Define Groups”定义框，在Group 1中输入“1”，在Group 2中输入“2”。 第三步：点击“Options”按钮弹出“Confidence Interval”定义框，在“Confidence Interval”框中输入“95”，点击“Continue”

第四步：单击“OK”按钮，得到输出结果。 输出结果表明：（假定两种方法组装产品的时间服从正态分布，且方差相等，两种方法组装产品所需时间差值的置信区间为[0.1403，7.2597]；假定两个总体的方差不相等，两种方法组装产品所需时间差值的置信区间为[0.1384， 7.2616]。）本例方差齐性检验结果：0.9170.05 =>=，不能拒绝原假设， pα 同方差假定是合理的，因而，两种方法组装产品所需时间差值的置信区间为（0.1403，7.2597）。 实验二： 一、实验目的 熟悉SPSS的参数估计功能，熟练掌握两个正态总体均值之差（匹配样本）的区间估计方法及操作过程，对SPSS运行结果能进行解释。 二、实验内容 【例】（数据文件为data03-2.sav）由10名学生组成一个随机样本，让他们分别采用A和B两套试卷进行测试。结果如表2所示： 表2 10名学生两套试卷的得分

正态总体参数的区间估计

第19讲 正态总体参数的区间估计 教学目的：理解区间估计的概念，掌握各种条件下对一个正态总体的均值和方差进行 区间估计的方法。 教学重点：置信区间的确定。 教学难点：对置信区间的理解。 教学时数： 2学时。 教学过程： 第六章 参数估计 §6.3正态总体参数的区间估计 1. 区间估计的概念 我们已经讨论了参数的点估计，但是对于一个估计量，人们在测量或计算时，常不以得到近似值为满足，还需估计误差，即要求知道近似值的精确程度。因此，对于未知参数θ，除了求出它的点估计?θ外，我们还希望估计出一个范围，并希望知道这个范围包含参数θ真值的可信程度。 设?θ为未知参数θ的估计量，其误差小于某个正数ε的概率为1(01)αα-<<，即 ?{||}1P θθεα -<=- 或 αεθθεθ-=+<<-1)??(P 这表明，随机区间)?,?(εθεθ+-包含参数θ真值的概率（可信程度）为1α-，则这个区间)?,?(εθεθ+-就称为置信区间，1α-称为置信水平。 定义 设总体X 的分布中含有一个未知参数θ。若对于给定的概率1(01)αα-<<，存在两个统计量1112(,,,)n X X X θθ= 与2212(,,,)n X X X θθ= ，使得 12{}1P θθθα <<=-

则随机区间12(,)θθ称为参数θ的置信水平为1α-的置信区间，1θ称为置信下限，2θ称为置信上限，1α-称为置信水平。 注（1）置信区间的含义：若反复抽样多次（各次的样本容量相等，均为n ），每一组样本值确定一个区间12(,)θθ，每个这样的区间要么包含θ的真值，要么不包含θ的真值。按伯努利大数定理，在这么多的区间中，包含θ真值的约占100(1)%α-，不包含θ真值的约仅占100%α。例如：若0.01α=，反复抽样1000次，则得到的1000个区间中，不包含θ真值的约为10个。 （2）置信区间的长度表示估计结果的精确性，而置信水平表示估计结果的可靠性。对于置信水平为1α-的置信区间12(,)θθ，一方面置信水平1α-越大，估计的可靠性越高；另一方面区间12(,)θθ的长度(2)ε越小，估计的精确性越好。但这两方面通常是矛盾的，提高可靠性通常会使精确性下降（区间长度变大），而提高精确性通常会使可靠性下降（1α-变小），所以要找两方面的平衡点。 在学习区间估计方法之前，我们先介绍标准正态分布的α分位点概念。 设 () ~0,1X N ，若 z α 满足条件 { },01 P X z α αα>=<<，则称点z α为标准正态分布的α分位点。例如求0.01z 。按照α分位点定义，我们有 {}0.010.01P X z >=，则{}0.010.99P X z ≤=，即0.01()0.99z φ=。查表可得0.01 2.327z =. 又 由()x ?图形的对称性知1z z αα-=-。下面列出了几个常用的z α值： 2. 正态总体均值μ的区间估计 设已给定置信水平为1α-，总体()2~,X N μσ，12,,,n X X X 为一个样本，2 ,X S 分别是样本均值和样本方差。

简述以样本均值估计总体均值的理由

估计理论 估计理论提供了从样本统计量估计未知总体参数的方法。样本统计量是某些测量值样本特征的经验性数值量度，不能将样本的经验抽样分布与样本理论抽样分布及总体概率分布混淆。（回顾：通俗解释“大数据”及推断性统计学：抽样分布） 两个概念 估计量：指任何一个对总体参数给出估计值的样本统计量，例如样本均值。 估计值：指从某一样本计算得到的估计量的一个具体数值。 点估计 对于来自一个测量总体的任何随机样本，如果对随机量（例如：样本的均值、方差或标准差）算得一个具体的数值（某个样本的均值、方差或标准差），用以估计总体的参数（例如：总体的均值、方差或标准差），则该数值称为总体参数（例如：总体的均值、方差或标准差）的一个点估计。 用点估计反映总体参数时，应该给出尽可能多的附加信息，使得便于评价估计值的准确度和精度。准确度受度量方法和抽样设计影响；精

度则由固定容量n的样本标准差决定，标准差越小越精确。 尽管有点估计及其准确度和精度的一些信息，但是仍然未能从样本跳跃到总体，即未能把点估计与待估总体参数联系起来，给出估计对参数的接近程度或确定在估计值中存在多大的可能误差，为了从样本信息推断总体参数，需要用到区间估计。 区间估计 区间估计是一个从样本到总体的推断，区间估计将总体参数置于一个实区间上。区间的边界值由三个因素决定： 1、样本点估计值； 2、联系总体参数和样本点估计的样本统计量（如Z统计量，做正态变换得到）； 3、该统计量的抽样分布（例如，样本均值的理论抽样分布服从正态分布，则Z统计量的抽样分布是标准正态分布）； 总体均值的区间估计公式推导

上述推导给出了总体均值的区间估计的概率形式，基于要求：容量为n的单样本来自无限大且标准差已知的正态分布总体。 置信水平 在进行数据分析时，经常需要输入置信水平，大多数情况选择95%