欧拉法matlab程序

1.Euler法

function [x,y]=naeuler(dyfun,xspan,y0,h) x=xspan(1):h:xspan(2);

y(1)=y0;

for n=1:length(x)-1

y(n+1)=y(n)+h*feval(dyfun,x(n),y(n)); end

x=x';y=y';

x1=0:0.2:1;y1=(1+2*x1).^0.5;

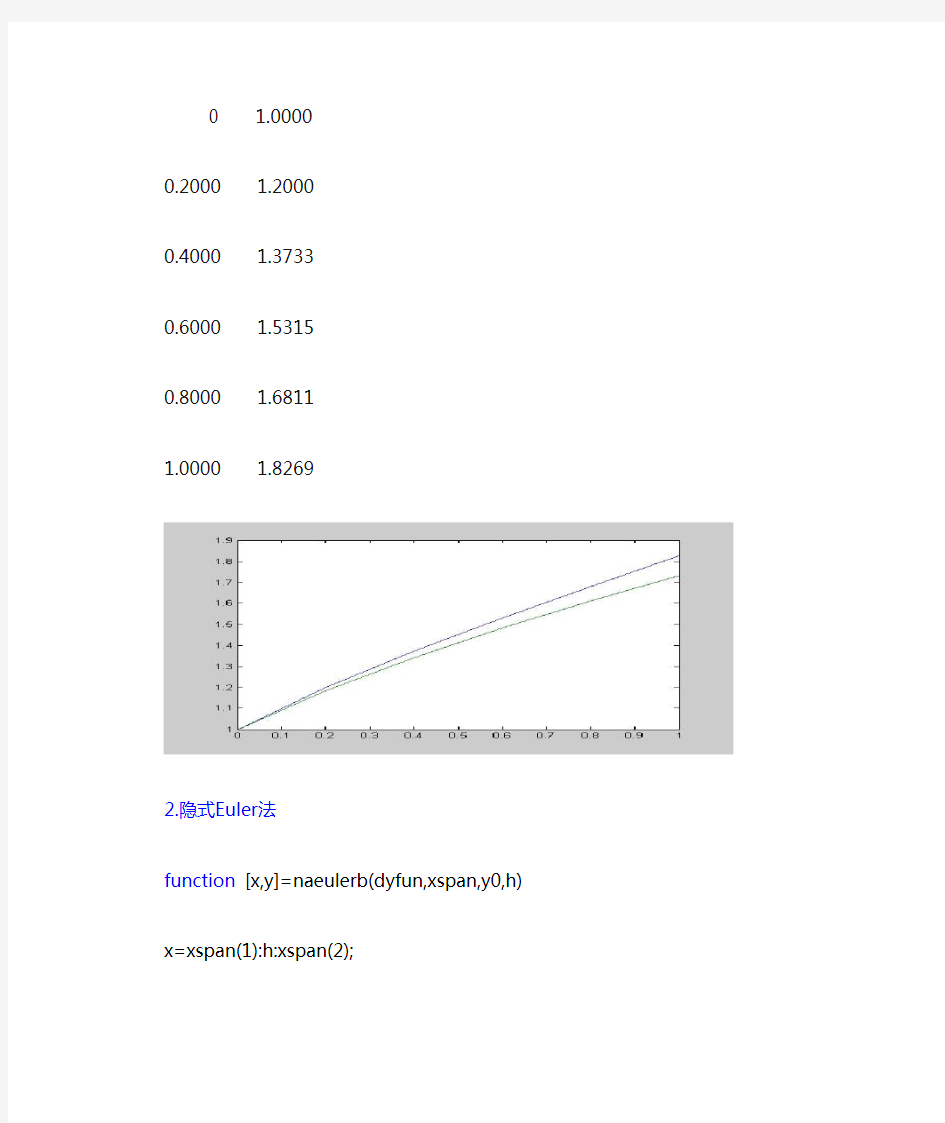
plot(x,y,x1,y1)

>> dyfun=inline('y-2*x/y');

[x,y]=naeuler(dyfun,[0,1],1,0.2);[x,y]

ans =

0 1.0000

0.2000 1.2000

0.4000 1.3733

0.6000 1.5315

0.8000 1.6811

1.0000 1.8269

2.隐式Euler法

function [x,y]=naeulerb(dyfun,xspan,y0,h) x=xspan(1):h:xspan(2);

y(1)=y0;

for n=1:length(x)-1

y(n+1)=iter(dyfun,x(n+1),y(n),h);

end

x=x';y=y';

x1=0:0.2:1;y1=(1+2*x1).^0.5;

plot(x,y,x1,y1)

function y=iter(dyfun,x,y,h)

y0=y;e=1e-4;K=1e+4;

y=y+h*feval(dyfun,x,y);

y1=y+2*e;k=1;

while abs(y-y1)>e

y1=y;

y=y0+h*feval(dyfun,x,y);

k=k+1;

if k>K

error('迭代发散');

end

end

>> dyfun=inline('y-2*x/y');

[x,y]=naeulerb(dyfun,[0,1],1,0.2);[x,y]

ans =

0 1.0000

0.2000 1.1641

0.4000 1.3014

0.6000 1.4146

0.8000 1.5019

1.0000 1.5561

3.改进Euler法

function [x,y]=naeuler2(dyfun,xspan,y0,h) x=xspan(1):h:xspan(2);

y(1)=y0;

for n=1:length(x)-1

k1=feval(dyfun,x(n),y(n));

y(n+1)=y(n)+h*k1;

k2=feval(dyfun,x(n+1),y(n+1));

y(n+1)=y(n)+h*(k1+k2)/2;

end

x=x';y=y';

x1=0:0.2:1;y1=(1+2*x1).^0.5;

plot(x,y,x1,y1)

>> dyfun=inline('y-2*x/y');

[x,y]=naeuler2(dyfun,[0,1],1,0.2);[x,y] ans =

0 1.0000

0.2000 1.1867

0.4000 1.3483

0.6000 1.4937

0.8000 1.6279

1.0000 1.7542

MATLAB代码 解线性方程组的迭代法

解线性方程组的迭代法 1.rs里查森迭代法求线性方程组Ax=b的解 function[x,n]=rs(A,b,x0,eps,M) if(nargin==3) eps=1.0e-6;%eps表示迭代精度 M=10000;%M表示迭代步数的限制值elseif(nargin==4) M=10000; end I=eye(size(A)); n=0; x=x0; tol=1; %迭代过程 while(tol>eps) x=(I-A)*x0+b; n=n+1;%n为最终求出解时的迭代步数tol=norm(x-x0); x0=x; if(n>=M) disp('Warning:迭代次数太多，可能不收敛！'); return; end end 2.crs里查森参数迭代法求线性方程组Ax=b的解 function[x,n]=crs(A,b,x0,w,eps,M) if(nargin==4) eps=1.0e-6;%eps表示迭代精度 M=10000;%M表示迭代步数的限制值 elseif(nargin==5) M=10000; end I=eye(size(A)); n=0; x=x0; tol=1; %迭代过程 while(tol>eps) x=(I-w*A)*x0+w*b; n=n+1;%n为最终求出解时的迭代步数tol=norm(x-x0); x0=x;

if(n>=M) disp('Warning:迭代次数太多，可能不收敛！'); return; end end 3.grs里查森迭代法求线性方程组Ax=b的解 function[x,n]=grs(A,b,x0,W,eps,M) if(nargin==4) eps=1.0e-6;%eps表示迭代精度 M=10000;%M表示迭代步数的限制值 elseif(nargin==5) M=10000; end I=eye(size(A)); n=0; x=x0; tol=1;%前后两次迭代结果误差 %迭代过程 while(tol>eps) x=(I-W*A)*x0+W*b;%迭代公式 n=n+1;%n为最终求出解时的迭代步数tol=norm(x-x0); x0=x; if(n>=M) disp('Warning:迭代次数太多，可能不收敛！'); return; end end 4.jacobi雅可比迭代法求线性方程组Ax=b的解 function[x,n]=jacobi(A,b,x0,eps,varargin) if nargin==3 eps=1.0e-6; M=200; elseif nargin<3 error return elseif nargin==5 M=varargin{1}; end D=diag(diag(A));%求A的对角矩阵 L=-tril(A,-1);%求A的下三角阵

实验五 欧拉法Matlab实验报告

北京理工大学珠海学院实验报告 ZHUHAI CAMPAUS OF BEIJING INSTITUTE OF TECHNOLOGY 班级2012电气2班学号120109021010姓名陈冲指导教师张凯成绩 实验题目（实验五）欧拉法实验地点及时间JD501 2014/1/2（6-7节） 一、实验目的 1.掌握用程序语言来编辑函数。 2.学会用MATLAB编写Euler.m以及TranEuler.m函数。 二、实验环境 Matlab软件 三、实验内容 1、以书中第124页题目11为例编辑程序来实现计算结果。 2、使用MATLAB进行编写： 第一步：编写Euler.m函数，代码如下 编写TranEuler.m函数，代码如下 第二步：利用上述函数编辑命令：（可见实验结果中的截图）

在此之前先建立一个名为f.m 的M 文件，代码如下 function z=f(x); z=8-3y; 再编辑代码： 得到了欧拉法的结果：y （0.4）=2.47838030901267 编辑另一段命令： 得到改进欧拉法的结果：y （0.4）=2.46543714659780 在此基础上，我还编辑龙格库达的命令窗口代码，如下： 四、实验题目 用欧拉法和改进欧拉法求解初值问题'83,(0)2y y y =-=，试取步长0.2h =计算(0.4)y 的近似值。 五、实验结果

六、总结 通过这次实验我掌握了将得到的解进一步精确，而且要学会比较这几种方法的精确性，显然，四阶龙格库达比改进欧拉发精确，改进欧拉发比欧拉法精确。 实验难度不大，要比较n的取值不同，产生的影响不同。

欧拉法matlab程序

法 function [x,y]=naeuler(dyfun,xspan,y0,h) x=xspan(1):h:xspan(2); y(1)=y0; for n=1:length(x)-1 y(n+1)=y(n)+h*feval(dyfun,x(n),y(n)); end x=x';y=y'; x1=0::1;y1=(1+2*x1).^; plot(x,y,x1,y1) >> dyfun=inline('y-2*x/y'); [x,y]=naeuler(dyfun,[0,1],1,;[x,y] ans = 2.隐式Euler法 function [x,y]=naeulerb(dyfun,xspan,y0,h) x=xspan(1):h:xspan(2); y(1)=y0; for n=1:length(x)-1 y(n+1)=iter(dyfun,x(n+1),y(n),h); end x=x';y=y'; x1=0::1;y1=(1+2*x1).^; plot(x,y,x1,y1) function y=iter(dyfun,x,y,h) y0=y;e=1e-4;K=1e+4; y=y+h*feval(dyfun,x,y); y1=y+2*e;k=1; while abs(y-y1)>e y1=y; y=y0+h*feval(dyfun,x,y); k=k+1; if k>K error('迭代发散'); end end >> dyfun=inline('y-2*x/y');

[x,y]=naeulerb(dyfun,[0,1],1,;[x,y] ans = 3.改进Euler法 function [x,y]=naeuler2(dyfun,xspan,y0,h) x=xspan(1):h:xspan(2); y(1)=y0; for n=1:length(x)-1 k1=feval(dyfun,x(n),y(n)); y(n+1)=y(n)+h*k1; k2=feval(dyfun,x(n+1),y(n+1)); y(n+1)=y(n)+h*(k1+k2)/2; end x=x';y=y'; x1=0::1;y1=(1+2*x1).^; plot(x,y,x1,y1) >> dyfun=inline('y-2*x/y'); [x,y]=naeuler2(dyfun,[0,1],1,;[x,y] ans =

高斯-赛德尔迭代法matlab程序

disp('划分为M*M个正方形') M=5 %每行的方格数，改变M可以方便地改变剖分的点数 u=zeros(M+1);%得到一个（M+1）*（M+1）的矩阵 disp('对每个剖分点赋初值，因为迭代次数很高，所以如何赋初值并不重要，故采用对列线性赋值。') disp('对边界内的点赋初值并使用边界条件对边界赋值：') for j=1:M-1 for i=1:M-1 u(i+1,j+1)=100*sin(pi/M*j)/M*(M-i);%对矩阵（即每个刨分点）赋初值 end end for i=1:M+1 u(1,i)=100*sin(pi*(i-1)/M);%使用边界条件对边界赋值 u(1,M+1)=0; end u tic %获取运行时间的起点 disp('迭代次数为N') N=6 %迭代次数，改变N可以方便地改变迭代次数 disp('n为当前迭代次数，u为当前值，结果如下：') for n=1:N for p=2:M i=M+2-p; for j=2:M u(i,j)=0.25*(u(i,j-1)+u(i+1,j)+u(i-1,j)+u(i,j+1));%赛德尔迭代法 end end n %输出n u %输出u end disp('所用的时间：') t=toc %获取算法运行需要的时间 [x,y]=meshgrid(0:1/M:1,0:1/M:1); z=u(1,:); for a=2:M+1 z=[z;u(a,:)];%获取最终迭代的结果，幅值给z，z的值代表该点的点位值 end mesh(x,y,z)%绘制三维视图以便清楚地显示结果 mesh(x,y,z,'FaceColor','white','EdgeColor','black') %绘制三维视图以便清楚地显示结果

matlab 欧拉算法 附截图

设系统方程为：y t y y /2)1(-=,1)0(=y ,用改进欧拉法求解各离散点y 的数值解，步长 10,1.0≤≤=t h ，解析解为t y 21+= 。 解：改进欧拉法 ),(1n n n p n y t hf y y +=+ )],(),([5.0111p n n n n n c n y t f y t f h y y +++++= 已知 n n n n n y t y y t f /2),(-= n n n n n n n p n y ht y h y t y h y y /2)1()/2(1-+=-+=+ 1 111111/5.0/)5.01()]/2()/2[(5.0+++++++-+-+=-+-+=n n n n n n n n n n n n n c n y ht hy y ht y h y t y y t y h y y 程序： h=0.1; t=0:h:1; N=length(t); y=ones(1,N); ey=ones(1,N); zy=ones(1,N); for k=1:N-1 y(1,k+1)=(1+h)*y(1,k)-(2*h*(k-1)/(N-1))./y(1,k);%预估公式 ey(1,k+1)=(1+h)*ey(1,k)-(2*h*(k-1)/(N-1))./ey(1,k);%欧拉公式 y(1,k+1)=(1+0.5*h)*y(1,k)-(h*(k-1)/(N-1))./y(1,k)+0.5*h*y(1,k+1)-(h*k/(N-1))./y(1,k+1);%改进欧拉 zy(1,k+1)=(1+2*k/(N-1)).^0.5;%解析解 end plot(t,zy,'-xk',t,y,':ob',t,ey,'-.*r','linewidth',1.0); xlabel('t'); ylabel('y'); 截图：

数值分析的MATLAB程序

列主元法 function lianzhuyuan(A,b) n=input('请输入n:') %选择阶数A=zeros(n,n); %系数矩阵A b=zeros(n,1); %矩阵b X=zeros(n,1); %解X for i=1:n for j=1:n A(i,j)=(1/(i+j-1)); %生成hilbert矩阵A end b(i,1)=sum(A(i,:)); %生成矩阵b end for i=1:n-1 j=i; top=max(abs(A(i:n,j))); %列主元 k=j; while abs(A(k,j))~=top %列主元所在行 k=k+1; end for z=1:n %交换主元所在行a1=A(i,z); A(i,z)=A(k,z); A(k,z)=a1; end a2=b(i,1); b(i,1)=b(k,1); b(k,1)=a2; for s=i+1:n %消去算法开始m=A(s,j)/A(i,j); %化简为上三角矩阵 A(s,j)=0; for p=i+1:n A(s,p)=A(s,p)-m*A(i,p); end b(s,1)=b(s,1)-m*b(i,1); end end X(n,1)=b(n,1)/A(n,n); %回代开始 for i=n-1:-1:1 s=0; %初始化s for j=i+1:n s=s+A(i,j)*X(j,1);

end X(i,1)=(b(i,1)-s)/A(i,i); end X 欧拉法 clc clear % 欧拉法 p=10; %贝塔的取值 T=10; %t取值的上限 y1=1; %y1的初值 r1=1; %y2的初值 %输入步长h的值 h=input('欧拉法please input number(h=1 0.5 0.25 0.125 0.0625):h=') ; if h>1 or h<0 break end S1=0:T/h; S2=0:T/h; S3=0:T/h; S4=0:T/h; i=1; % 迭代过程 for t=0:h:T Y=(exp(-t)); R=(1/(p-1))*exp(-t)+((p-2)/(p-1))*exp(-p*t); y=y1+h*(-y1); y1=y; r=r1+h*(y1-p*r1); r1=r; S1(i)=Y; S2(i)=R; S3(i)=y; S4(i)=r; i=i+1; end t=[0:h:T]; % 红线为解析解，'x'为数值解 plot(t,S1,'r',t,S3,'x')

lu分解法、列主元高斯法、jacobi迭代法、gaussseidel法的原理及matlab程序

一、实验目的及题目 1.1 实验目的： （1）学会用高斯列主元消去法，LU 分解法，Jacobi 迭代法和Gauss-Seidel 迭代法解线性方程组。 （2）学会用Matlab 编写各种方法求解线性方程组的程序。 1.2 实验题目： 1. 用列主元消去法解方程组： 1241234 123412343421233234x x x x x x x x x x x x x x x ++=??+-+=??--+=-??-++-=? 2. 用LU 分解法解方程组,Ax b =其中 4824012242412120620266216A --?? ?- ?= ? ?-??，4422b ?? ? ?= ?- ?-?? 3. 分别用Jacobi 迭代法和Gauss-Seidel 迭代法求解方程组： 123234 1231234102118311210631125x x x x x x x x x x x x x -+=-??-+=-??-+=??-+-+ =? 二、实验原理、程序框图、程序代码等 2.1实验原理 2.1.1高斯列主元消去法的原理 Gauss 消去法的基本思想是一次用前面的方程消去后面的未知数，从而将方程组化为等价形式： 1111221122222n n n n nn n n b x b x b x g b x b x g b x g +++=??++=????= ? 这个过程就是消元，然后再回代就好了。具体过程如下： 对于1,2, ,1k n =-，若() 0,k kk a ≠依次计算

()() (1)()()(1)()()/,,1, ,k k ik ik kk k k k ij ij ik kj k k k i i ik k m a a a a m a b b m b i j k n ++==-=-=+ 然后将其回代得到： ()() ()()()1/()/,1,2,,1 n n n n nn n k k k k k kj j kk j k x b a x b a x a k n n =+?=??=-=--? ? ∑ 以上是高斯消去。 但是高斯消去法在消元的过程中有可能会出现() 0k kk a =的情况，这时消元就无法进行了，即使主元数() 0,k kk a ≠但是很小时，其做除数，也会导致其他元素数量级的严重增长和舍入误差的扩散。因此，为了减少误差，每次消元选取系数矩阵的某列中绝对值最大的元素作为主元素。然后换行使之变到主元位置上，再进行销元计算。即高斯列主元消去法。 2.1.2直接三角分解法（LU 分解）的原理 先将矩阵A 直接分解为A LU =则求解方程组的问题就等价于求解两个三角形方程组。 直接利用矩阵乘法，得到矩阵的三角分解计算公式为： 1111111 11 1,1,2,,/,2,,,,,1,,,2,3, ()/,1,2, ,i i i i k kj kj km mj m k ik ik im mk kk m u a i n l a u i n u a l u j k k n k n l a l u u i k k n k n -=-===?? ==?? =-=+??=??=-=++≠?? ∑∑且 由上面的式子得到矩阵A 的LU 分解后，求解Ux=y 的计算公式为 11 111,2,3,/()/,1,2, ,1 i i i ij j j n n nn n i i ij j ii j i y b y b l y i n x y u x y u x u i n n -==+=??? =-=?? =??? =-=--?? ∑∑ 以上为LU 分解法。

Euler法解微分方程-Matlab程序

%主程序main.m-----OK! clear; T=0.0; Y=zeros(3,1); Y(1)=1.0;Y(2)=1.0;Y(3)=1.0; H1=0.05;M=3;EPS=1.0e-05;%EPS精度要求M方程个数H1拟定的输出步长 for i=1:10 [X,Y]=euler1(T,H1,Y,M,EPS) T=T+H1; End %变步长euler方法 function [X,Y1]=euler1(T,H1,Y,M,EPS) %M-方程个数,EPS-精度,Y0-右端初值，T-自变量前一点值，H-步长 N=1;P=1+EPS;X=T;G=zeros(M,1); H=H1;%H-在程序中要改变的步长H1－主程序中确定的输出步长 for i=1:M C(i)=Y(i); end K1=zeros(M,1);K2=zeros(M,1);K3=zeros(M,1);K4=zeros(M,1); while P>=EPS %变步长积分一步（H1） for i=1:M G(i)=Y(i); Y(i)=C(i); end DT=H/N; T=X; %－－变步长积分过程 for j=1:N K1=F(Y); K2=F(Y+H/2*K1'); K3=F(Y+H/2*K2'); K4=F(Y+H*K3'); for i=1:M Y(i)=Y(i)+H/6*(K1(i)+2*K2(i)+2*K3(i)+K4(i)); T=T+DT; end end %－－－－－－－－－－－－－－－－－－－－－ P=0.0; for i=1:M Q=abs(Y(i)-G(i)); if Q>P

P=Q; end end H=H/2.0; N=N+N; end T=X; X=T+H1; Y1=Y; %右端函数值function D=F(y) D(1)=y(2); D(2)=-1*y(1); D(3)=y(3);

MATLAB改进欧拉法与四阶龙格-库塔求解一阶常微分方程

姓名：樊元君学号：2012200902 日期：2012.11.06 一、实验目的 掌握MATLAB语言、C/C++语言编写计算程序的方法、掌握改进欧拉法与四阶龙格-库塔求解一阶常微分方程的初值问题。掌握使用MATLAB程序求解常微分方程问题的方法。 二、实验内容 1、分别写出改进欧拉法与四阶龙格-库塔求解的算法，编写程序上机调试出结果，要求所编程序适用于任何一阶常微分方程的数值解问题，即能解决这一类问题，而不是某一个问题。 实验中以下列数据验证程序的正确性。 求，步长h=0.25。 2、实验注意事项 的精确解为，通过调整步长，观察结果的精度的变化

三、程序流程图： ●改进欧拉格式流程图：

●四阶龙格库塔流程图： 四、源程序： ●改进后欧拉格式程序源代码：

format long h=input('h='); x0=input('x0='); y0=input('y0='); disp('输入的范围是：'); X=input('X=');Y=input('Y='); n=round((Y-X)/h); i=1;x1=0;yp=0;yc=0; for i=1:1:n x1=x0+h; yp=y0+h*(-x0*(y0)^2);%yp=y0+h*(y0-2*x0/y0);% yc=y0+h*(-x1*(yp)^2);%yc=y0+h*(yp-2*x1/yp);% y1=(yp+yc)/2; x0=x1;y0=y1; y=2/(1+x0^2);%y=sqrt(1+2*x0);% fprintf('结果=%.3f,%.8f,%.8f\n',x1,y1,y); end end ●四阶龙格库塔程序源代码：

MATLAB Euler法解常微分方程

Euler 法解常微分方程 Euler 法解常微分方程算法： Step 1 分别取积分上限、积分下限、步长 Step 2计算h n n +=判断b n ≤是否成立，成立转到Step 3，否则继续进行Step 4 Step 3 计算),(1n n n n y x hf y y +=+ Step 4 ),(1n n n n y x hf y y +=+ Euler 法解常微分方程算程序： function euler2(fun,y0,A,h) %fun--y' %y0---初值 %A----x 取值范围 %a----x 左区间端点值 %b----x 右区间端点值 %h----给定步长 x=min(A); b=max(A); y=y0; while x

0.4613 指导教师： 年 月 日 改进Euelr 法解常微分方程 改进Euler 法解常微分方程算法： Step 1 分别取积分上限、积分下限、步长 Step 2 取一个以h 为步长，a ，b 分别为左右端点的矩阵 Step 3 （1）做显性Euler 预测),( 1n n i i y x hf y y +=+ （2）将1+i y 带入,(),([2h 11++++=i i i i i x f y x f y y Step 4计算h n n +=判断b n ≤是否成立，成立返回Step 5 )],(),([2h 111+++++=i i i i i i y x f y x f y y 改进Euler 法解常微分方程算程序： function gaijineuler2(fun,y0,A,h) %fun--y' %y0---初值 %A----x 取值范围 %a----x 左区间端点值 %b----x 右区间端点值 %h----给定步长 a=min(A); b=max(A); x=a:h:b; y(1)=y0; for i=1:length(x)-1 w1=feval(fun,x(i),y(i)); y(i+1)=y(i)+h*w1; w2=feval(fun,x(i+1),y(i+1)); y(i+1)=y(i)+h*(w1+w2)/2; end x=x'

matlab 迭代法[精品]

matlab 迭代法[精品] 1. 矩阵 122,211,，，，，,,,,A,111A,222, 11,,,,,,,,221,,112，，，， 证明:求解以为系数矩阵线性方程组的Jacobi迭代式收敛的，而A1 Gauss-Seidel方法是发散的;求解以为系数矩阵线性方程组的A2实验名称Gauss-Seidel是收敛的，而Jacobi方法是发散的. 2. 矩阵 1aa，，,,Aaa,1 ,,,,aa1，， (a) 参数取什么值时，矩阵是正定的. a (b) 取什么值时，求以为系数矩阵线性方程组的Jacobi迭代式收aa 敛的. 1、根据迭代收敛性的充分必要条件来判断Jacobi迭代式与Gauss-Seide 迭代式的收敛性，迭代收敛性仅与方程组系数矩阵有关，与右端无关;而且不依赖于初值的选取。实验目的 2、根据矩阵的判断定理求得矩阵元素a的取值，同时根据矩阵线性方程组的Jacobi迭代式收敛的充分条件(严格对角占优)来求a得取值。 1、(1)检验线性方程组的Jacobi迭代式的收敛性: function jacobi(A) D=zeros(3); for i=1:3 D(i,i)=A(i,i); 实验内容end (算法、程B=D^(-1)*(D-A); 序、步骤和k=max(abs(eig(B))) 方法) if k<1

'该线性方程组的Jacobi迭代式是收敛的' else k>=1 '该线性方程组的Jacobi迭代式是发散的' end (2)检验线性方程组的Gauss-Seide迭代式的收敛性: function Gauss(A) D=zeros(3); L=zeros(3); U=zeros(3); for i=1:3 D(i,i)=A(i,i); end L(2:3,1)=A(2:3,1); L(3,2)=A(3,2); U(1,2:3)=A(1,2:3); U(2,3)=A(2,3); B=-(D+L)^(-1)*U; k=max(abs(eig(B))) if k<1 '该线性方程组的Gauss-Seidel迭代式是收敛的' else k>=1 '该线性方程组的Gauss-Seidel迭代式是发散的' end 2、(1)参数取什么值时，矩阵是正定的.(矩阵的特征值全为正) a >> syms a >> A=[1 a a;a 1 a;a a 1]; >> eig(A) ans = 2*a+1 1-a

向前欧拉公式计算matlab程序函数

向前欧拉公式计算matlab程序函数 function [H,X,Y,k,h,P]=QEuler(funfcn,x0,b,y0,tol) %初始化. pow=1/3; if nargin < 5 | isempty(tol), tol = 1.e-6; end; x=x0; h=0.0078125*(b-x); y=y0(:); p=128; H=zeros(p,1); X=zeros(p,1); Y=zeros(p,length(y)); k=1; X(k)=x; Y(k,:)=y'; % 绘图. clc,x,h,y % end % 主循环. while (xx) if x+h>b h=b-x; end %计算斜率. fxy=feval(funfcn,x,y); fxy=fxy(:); %计算误差，设定可接受误差. delta=norm(h*fxy,'inf'); wucha=tol*max(norm(y,'inf'),1.0); % 当误差可接受时重写解. if delta<=wucha x=x+h; y=y+h*fxy; k=k+1; if k>length(X) X=[X;zeros(p,1)]; Y=[Y;zeros(p,length(y))]; H=[H;zeros(p,1)]; end H(k)=h;

X(k)=x; Y(k,:)=y'; plot(X,Y,'rp'), grid xlabel('自变量X'), ylabel('因变量Y') end %更新步长. if delta~=0.0 h=min(h*8,0.9*h*(wucha/delta)^pow); end end if (x

解微分方程欧拉法-R-K法及其MATLAB实例

欧拉方法（Euler method)用以对给定初值的常微分方程(即初值问题)求解 分为前进EULER法、后退EULER法、改进的EULER法。 缺点： 欧拉法简单地取切线的端点作为下一步的起点进行计算，当步数增多时，误差会因积累而越来越大。因此欧拉格式一般不用于实际计算。 改进欧拉格式： 为提高精度，需要在欧拉格式的基础上进行改进。采用区间两端的斜率的平均值作为直线方程的斜率。改进欧拉法的精度为二阶。 算法为： 微分方程的本质特征是方程中含有导数项，数值解法的第一步就是设法消除其导数值。 对于常微分方程： x∈[a,b] y(a) = y0 可以将区间[a,b]分成n段，那么方程在第xi点有y'(xi) = f(xi,y(xi))，再用向前差商近似代替导数则为： 在这里，h是步长，即相邻两个结点间的距离。因此可以根据xi点和yi点的数值计算出yi+1来： i=0,1,2,L 这就是向前欧拉格式。 改进的欧拉公式： 将向前欧拉公式中的导数f(xi,yi)改为微元两端导数的平均，即 上式便是梯形的欧拉公式。 可见，上式是隐式格式，需要迭代求解。为了便于求解，使用改进的欧拉公式：

数值分析中，龙格－库塔法（Runge-Kutta）是用于模拟常微分方程的解的重要的一类隐式或显式迭代法。 实际上，龙格-库塔法是欧拉方法的一种推广，向前欧拉公式将导数项简单取为f(xn,yn),而改进的欧拉公式将导数项取为两端导数的平均。 龙格-库塔方法的基本思想： 在区间[xn,xn+1]内多取几个点，将他们的斜率加权平均，作为导数的近似。 龙格库塔法的家族中的一个成员如此常用，以至于经常被称为“RK4”或者就是“龙格库塔法”。 令初值问题表述如下。 则，对于该问题的RK4由如下方程给出： 其中 这样，下一个值(y n+1)由现在的值(y n)加上时间间隔(h)和一个估算的斜率的乘积决定。该斜率是以下斜率的加权平均： k1是时间段开始时的斜率；

matlab迭代法代码

matlab 迭代法代码 1、％用不动点迭代法求方程x-e A x+4=0的正根与负根，误差限是 10A-6% disp(' 不动点迭代法 '); n0=100; p0=-5; for i=1:n0 p=exp(p0)-4; if abs(p-p0)<=10(6) if p<0 disp('|p-p0|=') disp(abs(p-p0)) disp(' 不动点迭代法求得方程的负根为 :') disp(p); break; else disp(' 不动点迭代法无法求出方程的负根 .') end else p0=p; end end

if i==n0 disp(n0) disp(' 次不动点迭代后无法求出方程的负根') end p1=1.7; for i=1:n0 pp=exp(p1)-4; if abs(pp-p1)<=10(6) if pp>0 disp('|p-p1|=') disp(abs(pp-p1)) disp(' 用不动点迭代法求得方程的正根为 ') disp(pp); else disp(' 用不动点迭代法无法求出方程的正根 '); end break; else p1=pp; end end if i==n0

disp(n0) disp(' 次不动点迭代后无法求出方程的正根 ') end 2、％用牛顿法求方程x-e A x+4=0的正根与负根，误差限是disp(' 牛顿法') n0=80; p0=1; for i=1:n0 p=p0-(p0-exp(p0)+4)/(1-exp(p0)); if abs(p-p0)<=10(6) disp('|p-p0|=') disp(abs(p-p0)) disp(' 用牛顿法求得方程的正根为 ') disp(p); break; else p0=p; end end if i==n0 disp(n0) disp(' 次牛顿迭代后无法求出方程的解 p1=-3; for i=1:n0 p=p1-(p1-exp(p1)+4)/(1-exp(p1)); 10A-6 ') end

欧拉法matlab程序

1.Euler法 function [x,y]=naeuler(dyfun,xspan,y0,h) x=xspan(1):h:xspan(2); y(1)=y0; for n=1:length(x)-1 y(n+1)=y(n)+h*feval(dyfun,x(n),y(n)); end x=x';y=y'; x1=0:0.2:1;y1=(1+2*x1).^0.5; plot(x,y,x1,y1) >> dyfun=inline('y-2*x/y'); [x,y]=naeuler(dyfun,[0,1],1,0.2);[x,y] ans = 0 1.0000 0.2000 1.2000 0.4000 1.3733 0.6000 1.5315 0.8000 1.6811 1.0000 1.8269 2.隐式Euler法 function [x,y]=naeulerb(dyfun,xspan,y0,h) x=xspan(1):h:xspan(2); y(1)=y0; for n=1:length(x)-1 y(n+1)=iter(dyfun,x(n+1),y(n),h); end x=x';y=y'; x1=0:0.2:1;y1=(1+2*x1).^0.5;

plot(x,y,x1,y1) function y=iter(dyfun,x,y,h) y0=y;e=1e-4;K=1e+4; y=y+h*feval(dyfun,x,y); y1=y+2*e;k=1; while abs(y-y1)>e y1=y; y=y0+h*feval(dyfun,x,y); k=k+1; if k>K error('迭代发散'); end end >> dyfun=inline('y-2*x/y'); [x,y]=naeulerb(dyfun,[0,1],1,0.2);[x,y] ans = 0 1.0000 0.2000 1.1641 0.4000 1.3014 0.6000 1.4146 0.8000 1.5019 1.0000 1.5561 3.改进Euler法 function [x,y]=naeuler2(dyfun,xspan,y0,h) x=xspan(1):h:xspan(2); y(1)=y0; for n=1:length(x)-1 k1=feval(dyfun,x(n),y(n)); y(n+1)=y(n)+h*k1; k2=feval(dyfun,x(n+1),y(n+1));

二分法、简单迭代法的matlab代码实现教学文案

二分法、简单迭代法的m a t l a b代码实现

实验一非线性方程的数值解法（一）信息与计算科学金融崔振威 201002034031 一、实验目的： 熟悉二分法和简单迭代法的算法实现。 二、实验内容： 教材P40 2.1.5 三、实验要求 1 根据实验内容编写二分法和简单迭代法的算法实现 2 简单比较分析两种算法的误差 3 试构造不同的迭代格式，分析比较其收敛性 (一)、二分法程序： function ef=bisect(fx,xa,xb,n,delta) % fx是由方程转化的关于x的函数，有fx=0。 % xa 解区间上限 % xb 解区间下限 % n 最多循环步数，防止死循环。 %delta 为允许误差 x=xa;fa=eval(fx); x=xb;fb=eval(fx); disp(' [ n xa xb xc fc ]'); for i=1:n xc=(xa+xb)/2;x=xc;fc=eval(fx); X=[i,xa,xb,xc,fc]; disp(X), if fc*fa<0 xb=xc; else xa=xc;

end if (xb-xa)eps & k> fplot('[x^5-3*x^3-2*x^2+2]',[-3,3]);grid 得下图：

迭代解法的matlab实现

解线性方程组b AX =的迭代法是从初始解出发，根据设计好的步骤用逐次求出的近似解逼近精确解.在第三章中介绍的解线性方程组的直接方法一般适合于A 为低阶稠密矩阵（指n 不大且元多为非零）的情况，而在工程技术和科学计算中常会遇到大型稀疏矩阵（指n 很大且零元较多）的方程组，迭代法在计算和存贮两方面都适合后一种情况.由于迭代法是通过逐次迭代来逼近方程组的解，所以收敛性和收敛速度是构造迭代法时应该注意的问题.另外，因为不同的系数矩阵具有不同的性态，所以大多数迭代方法都具有一定的适用范围.有时，某种方法对于一类方程组迭代收敛，而对另一类方程组迭代时就发散.因此，我们应该学会针对具有不同性质的线性方程组构造不同的迭代. 4.1 迭代法和敛散性及其MATLAB 程序 4.1.2 迭代法敛散性的判别及其MATLAB 程序 根据定理4.1和谱半径定义，现提供一个名为pddpb.m 的M 文件，用于判别迭代公H=eig(B);mH=norm(H,inf); if mH>=1 disp('请注意：因为谱半径不小于1，所以迭代序列发散,谱半径mH 和B 的所 有的特征值H 如下：') else disp('请注意：因为谱半径小于1，所以迭代序列收敛,谱半径mH 和B 的所有 的特征值H 如下：') end mH 4.1.3 与迭代法有关的MATLAB 命令 （一） 提取（产生）对角矩阵和特征值 可以用表4–1的MATLAB 命令提取对角矩阵和特征值. (二) 提取（产生）上（下）三角形矩阵

可以用表4–2的MATLAB命令提取矩阵的上三角形矩阵和下三角形矩阵. (三)稀疏矩阵的处理 对稀疏矩阵在存贮和运算上的特殊处理，是MA TLAB进行大规模科学计算时的特点和优势之一.可以用表4–3的MATLAB命令，输入稀疏矩阵的非零元（零元不必输入），即可进行运算. 4.2 雅可比（Jacobi）迭代及其MATLAB程序 4.2.2 雅可比迭代的收敛性及其MATLAB程序 [n m]=size(A); for j=1:m a(j)=sum(abs(A(:,j)))-2*(abs(A(j,j))); end for i=1:n if a(i)>=0 disp('请注意：系数矩阵A不是严格对角占优的，此雅可比迭代不一定收敛') return end end if a(i)<0 disp('请注意：系数矩阵A是严格对角占优的，此方程组有唯一解，且雅可比迭代收敛') end 例4.2.2 用判别雅可比迭代收敛性的MATLAB主程序，判别由下列方程组的雅可比迭

欧拉法matlab程序

1.Euler法 function[x,y]=naeuler(dyfun,xspan,y0,h) x=xspan(1):h:xspan(2); y(1)=y0; for n=1:length(x)-1 y(n+1)=y(n)+h*feval(dyfun,x(n),y(n)); end x=x';y=y'; function[x,y]=naeulerb(dyfun,xspan,y0,h) x=xspan(1):h:xspan(2); y(1)=y0; for n=1:length(x)-1 y(n+1)=iter(dyfun,x(n+1),y(n),h); end x=x';y=y'; x1=0:0.2:1;y1=(1+2*x1).^0.5; plot(x,y,x1,y1) >>dyfun=inline('y-2*x/y'); [x,y]=naeuler(dyfun,[0,1],1,0.2);[x,y] ans= 0 1.0000 0.2000 1.2000 0.4000 1.3733 0.6000 1.5315 0.8000 1.6811 1.0000 1.8269 2.隐式Euler法 function y=iter(dyfun,x,y,h) y0=y;e=1e-4;K=1e+4; y=y+h*feval(dyfun,x,y);

y1=y+2*e;k=1; while abs(y-y1)>e y1=y; y=y0+h*feval(dyfun,x,y); k=k+1; if k>K error('迭代发散'); end end >>dyfun=inline('y-2*x/y'); [x,y]=naeulerb(dyfun,[0,1],1,0.2);[x,y] ans= 0 1.0000 0.2000 1.1641 0.4000 1.3014 0.6000 1.4146 0.8000 1.5019 1.0000 1.5561 3.改进Euler法 function[x,y]=naeuler2(dyfun,xspan,y0,h) x=xspan(1):h:xspan(2); y(1)=y0; for n=1:length(x)-1 k1=feval(dyfun,x(n),y(n)); y(n+1)=y(n)+h*k1; k2=feval(dyfun,x(n+1),y(n+1)); y(n+1)=y(n)+h*(k1+k2)/2; end x=x';y=y'; >>dyfun=inline('y-2*x/y');

MATLABEuler法解常微分方程

Euler法解常微分方程 Euler法解常微分方程算法： Step 1 分别取积分上限、积分下限、步长 Step 2计算判断是否成立，成立转到Step 3，否则继续进行Step 4 Step 3 计算 Step 4 Euler法解常微分方程算程序： function euler2(fun,y0,A,h) %fun--y' %y0---初值 %A----x取值范围 %a----x左区间端点值 %b----x右区间端点值 %h----给定步长 x=min(A); b=max(A); y=y0; while x

Step 3 （1）做显性Euler预测 （2）将带入 Step 4计算判断是否成立，成立返回Step 3，否则继续进行Step 5 Step 5 改进Euler法解常微分方程算程序： function gaijineuler2(fun,y0,A,h) %fun--y' %y0---初值 %A----x取值范围 %a----x左区间端点值 %b----x右区间端点值 %h----给定步长 a=min(A); b=max(A); x=a:h:b; y(1)=y0; for i=1:length(x)-1 w1=feval(fun,x(i),y(i)); y(i+1)=y(i)+h*w1; w2=feval(fun,x(i+1),y(i+1)); y(i+1)=y(i)+h*(w1+w2)/2; end x=x' y=y' 例：用改进Euler法计算下列初值问题（取步长h=0.25） 输入：fun=inline('-x*y^2') gaijineuler2(fun,2,[0 5],0.25) 得到： x = 0.2500 0.5000 0.7500 1.0000 1.2500 1.5000 1.7500 2.0000 2.2500 2.5000 2.7500