第3章习题 波(答案)

第3章波动部分习题(答案)
一、选择题
1. 一平面简谐波表达式为)2(sin 05.0x t y --=π (SI) ,则该波的频率v (Hz)、波速u (m ?s -1)及波线上各点振动的振幅A (m)依次为:[ C ]
(A) 2/1,2/1,05.0- (B) 2/1,1,05.0- (C) 2/1,2/1,05.0 (D) 2 ,2,05.0
解:平面简谐波表达式可改写为
)2(sin 05.0x t y --=π
与标准形式的波动方程 ])(2[cos ?π+-=u
x
t v A y 比较,可得
)s (m 2
1
,(Hz)21,
(m)05.01-?===u v A 。 2. 一横波沿绳子传播时的波动方程为)104cos(05.0t x y ππ-= (SI),则 [ A ] (A) 其波长为0.5 m ; (B) 波速为5 m ?s -1 ;
(C) 波速25 m ?s -1 ; (D) 频率2 Hz 。
解:将波动方程与标准形式 ])(2[cos ?π+-=u x t v A y 比较,????
?
?
???
?-
=)4(10cos 05.0πππx
t y )s m (5.2),Hz (51-?==u v )m (5.05
5
.2==
=v u λ 3. 一平面简谐波的波动方程为)3cos(1.0πππ+-=x t y (SI),t = 0时的波形曲线如图所示。则[ C ] (A) O 点的振幅为-0.1 m ; (B) 波长为3 m ;
(C) a 、b 两点位相差 π2
1
;
(D) 波速为9 m ?s -1。
解:由波动方程可知??
?
???+-=ππ)3(3cos 1.0x t y
(Hz),2
3
(m),1.0=
=νA )s (m 31-?=u ,(m)2=λ, a 、b 两点间相位差为:2
422πλλ
π
λ
π
?===?ab
4. 一简谐波沿x 轴负方向传播,圆频率为ω,波速为u 。设t = T /4时刻的波形如图所示,则该波的表
达式为: [ D ] )/(cos (A)u x t A y -=ω ]2)/(c o s [(B )π
ω+-=u x t A y )]/(cos[(C)u x t A y +=ω ])/(c o s [(D )πω++=u x t A y
解:设波方程为])/(cos[?ω++=u x t A y ,只有?不知道。求?有两种方法,
(1) 把4/,0T t x ==代入,此时O 的相位应该为π-。
(2) 把波往回推4/T ,如图所示,为零时刻的波形图,把0,0==t x 代入,此时O 的相位应该为π-
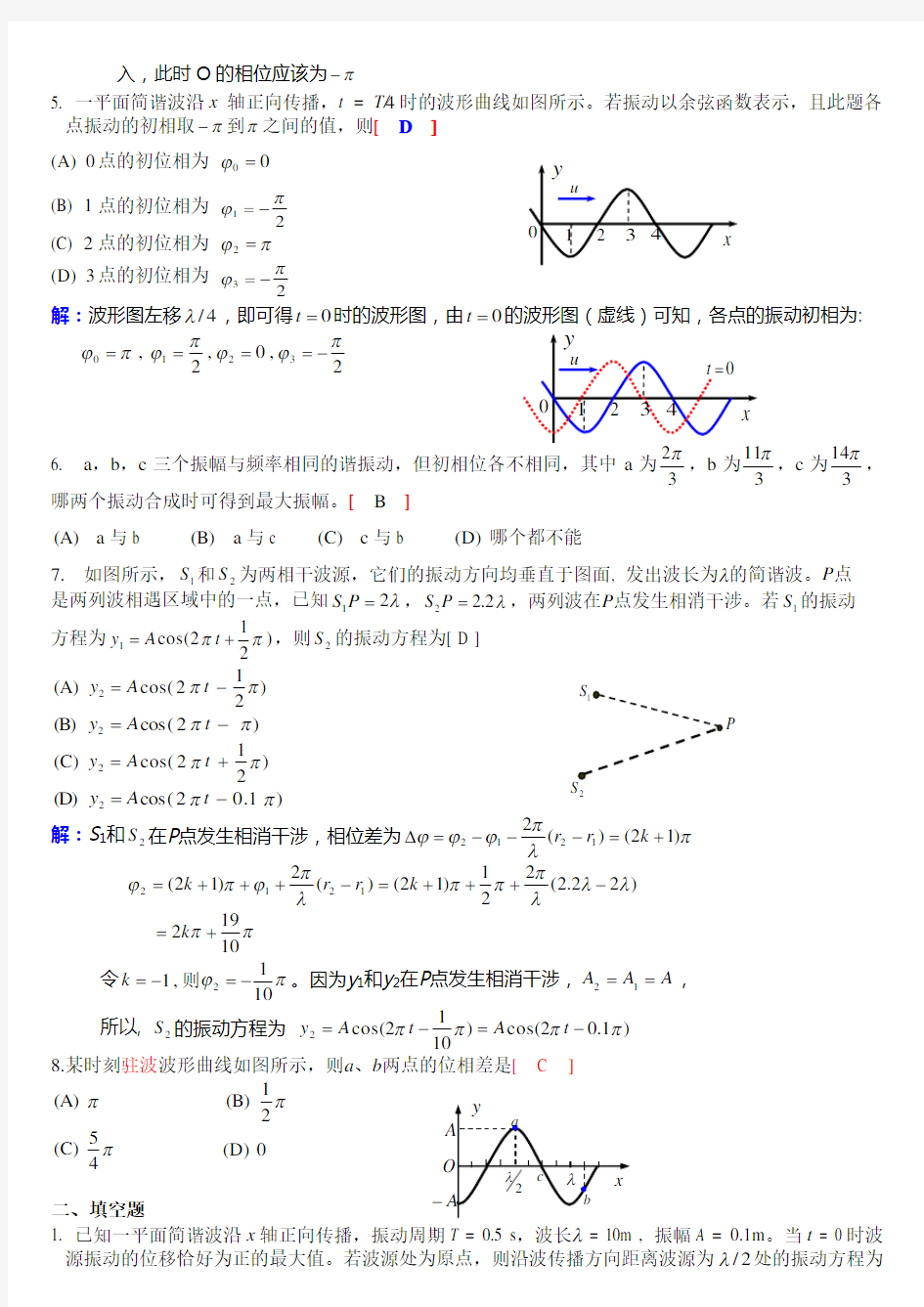
5. 一平面简谐波沿x 轴正向传播,t = T/4时的波形曲线如图所示。若振动以余弦函数表示,且此题各
点振动的初相取π-到π之间的值,则[ D ] (A) 0点的初位相为 00=? (B) 1点的初位相为 2
1π
?-
=
(C) 2点的初位相为 π?=2 (D) 3点的初位相为 2
3π?-=
解:波形图左移4/λ,即可得0=t 时的波形图,由0=t 的波形图(虚线)可知,各点的振动初相为:
2,0,2,3210π
??π?π?-====
6. a ,b ,c 三个振幅与频率相同的谐振动,但初相位各不相同,其中a 为3
,b 为3,c 为3
14
π
,
哪两个振动合成时可得到最大振幅。[ B ]
(A) a 与b (B) a 与c (C) c 与b (D)
哪个都不能
7. 如图所示,1S 和2S 为两相干波源,它们的振动方向均垂直于图面, 发出波长为λ的简谐波。P 点是两列波相遇区域中的一点,已知λ21=P S ,λ2.22=P S ,两列波在P 点发生相消干涉。若1S 的振动
方程为)21
2(cos 1ππ+=t A y ,则2S 的振动方程为[ D ]
)2
1
2(cos (A)2ππ-=t A y )2(cos (B)2ππ-=t A y
)2
1
2(cos (C)2ππ+=t A y
)1.02(cos (D)2ππ-=t A y
解:S 1和2S 在P 点发生相消干涉,相位差为πλ
π
???)12()(21212+=---=?k r r )(2)12(1212r r k -+++=λπ?π?)22.2(221)12(λλλ
π
ππ-+++=k
ππ10
19
2+=k
令π?10
1
,12-=-=则k 。因为y 1和y 2在P 点发生相消干涉,A A A ==12,
所以, 2S 的振动方程为 )1.02cos()10
1
2cos(2ππππ-=-=t A t A y
8.某时刻驻波波形曲线如图所示,则a 、b 两点的位相差是[ C ]
π(A) π21
(B ) π45
(C) 0(D)
二、填空题
1. 已知一平面简谐波沿x 轴正向传播,振动周期T = 0.5 s ,波长λ = 10m , 振幅A = 0.1m 。当t = 0时波源振动的位移恰好为正的最大值。若波源处为原点,则沿波传播方向距离波源为2/λ处的振动方程为(SI))4(cos 1.0ππ-=t y 。当 t = T / 2时,4/λ=x 处质点的振动速度为1s m 26.1-?-。
2
解:波动方程为(SI))20(4cos 1.0])(cos[?????
?
-=+-=x t u x t A y π?ω,
m 52==λ
x 处的质点振动方程为 )4cos(1.0ππ-=t y (SI)
m 5.24==λx 处的振动方程为)4sin(1.0)2
4cos(1.0t t y ππ
π=-=
振动速度 )4cos(4.0)4cos(41.0d d t t t
y
v ππππ=?==
s 25.02
==
T t 时 )s (m 26.14.0)25.04cos(4.01
-?-=-=?=πππv
2. 一简谐波沿 x 轴正向传播。1x 和2x 两点处的振动曲线分别如图(a) 和
所示。已知 12x x > 且 λ
<-12x x (λ为波长),则2x 点的相位1x 比点相位滞后 3π/2
。
解:由图(a)、(b)可知,1x 和2x 处振动初相分别为:
π?231=
,02=?二点振动相位差为π???2
3
21=-=? 因为λ<->1212,x x x x ,所以2x 的相位比1x 的相位滞后π2
3
。
3. 图示一平面简谐波在 t = 2 s 时刻的波形图,波的振幅为 0.2 m ,周期为4 s 。则图中P 点处质点的振动方程为)(SI)2
1
21cos(2.0ππ-=t y p
解:画出零时刻的波形图:P 点的初相位为2
π
-
)2c o s (|πω
-=t A y P )242c o s (2.0ππ-=t )2
1
21c o s (2.0ππ-=t (SI )
4. 图(a )为波源的振动曲线,此振动以波速s m u /20=向X 轴正方向传播。若以波源处作为坐标原点,根据图中数据,此简谐波的波动方程为 图(b )为一简谐波某时刻的波形图,若以此时刻作为起始时刻,并已知波速s m u /5=,此波的波动方程为 。 ]2
)20(2cos[π
π--=x t T A y
]2
)5(10cos[π
λπ--=x t A y
5. 两相干波源1S 和2S 的振动方程分别是 t A y ωcos 1=和)2
1(cos 2πω+=t A y 。 1S 距P 点3个波长, 2S 距P 点4/21个波长。两波在P 点引起的两个振动的相位差的绝对值是π4 。 解:两相干波在P 点的相位差为:
A O
y y
πλλλππλ
π
???4)34
21(2021)(21212-=---=
--
-=?r r π?4=?
作业题3
3-1.原长为m 5.0的弹簧,上端固定,下端挂一质量为kg 1.0的物体,当物体静止时,弹簧长为m 6.0.现将物体上推,使弹簧缩回到原长,然后放手,以放手时开始计时,取竖直向下为正向,写出振动式。(g 取9.8) 解:振动方程:cos()x A t ω?=+,在本题中,kx mg =,所以9.8k =;
∴ ω=
==。 取竖直向下为x 正向,弹簧伸长为0.1m 时为物体的平衡位置,所以如果使弹簧的初状态为原长,那么:A =0.1m , 当t =0时,x =-A ,那么就可以知道物体的初相位为π。
所以:0.1cos x π=+)
即:)x =- 3-4.两质点作同方向、同频率的简谐振动,振幅相等。当质点1在 2/1A x =处,且向左运动时,另一个质点2在
2/2A x -= 处,且向右运动。求这两个质点的位相差。
解:由旋转矢量图可知:
当质点1在 2/1A x =处,且向左运动时, 相位为
3
π, 而质点2在 2/2A x -= 处,且向右运动, 相位为
43
π。 所以它们的相位差为π。
3-9.沿一平面简谐波的波线上,有相距2.0m 的两质点A 与B ,B 点振动相位比A 点落后6
π
,已知振动周期为2.0s ,求波长和波速。
解:根据题意,对于A 、B 两点,m x A B 26=?-
=-=?,π
???,
而相位和波长之间满足关系:πλ
πλ???22x
x x A B
A B ?-=--=-=?, 代入数据,可得:波长λ=24m 。又∵T =2s ,所以波速12/u m s T
λ
=
=。
3-10.已知一平面波沿x 轴正向传播,距坐标原点O 为1x 处P 点的振动式为)cos(?ω+=t A y ,波速为u ,求:
(1)平面波的波动式;
(2)若波沿x 轴负向传播,波动式又如何?
解:(1)设平面波的波动式为0cos[]x
y A t u
ω
?=-+(),则P 点的振动式为: 1
0cos[]P x y A t u
ω?=-
+(),与题设P 点的振动式cos()P y A t ω?=+比较, 有:10x u
ω??=+,∴平面波的波动式为:1
cos[()]x x y A t u ω?-=-+;
(2)若波沿x 轴负向传播,同理,设平面波的波动式为:0cos[]x
y A t u
ω?=++(),则P 点的振动式为: 10cos[]P x
y A t u ω?=++(),与题设P 点的振动式cos()P y A t ω?=+比较,
有:10x u ω??=-+,∴平面波的波动式为:1
cos[()]x x y A t u ω?-=++。
3-12.已知一沿x 正方向传播的平面余弦波,s 3
1
=
t 时的波形如图所示,且周期T 为s 2。 (1)写出O 点的振动表达式;
(2)写出该波的波动表达式; (3)写出A 点的振动表达式; (4)写出A 点离O 点的距离。
解:由图可知:0.1A m =,0.4m λ=,而2T s =,
则:/0.2/u T m s λ==,
2T πωπ=
=,25k ππλ
==,∴波动方程为:00.1cos(5)y t x ππ?=-+ O 点的振动方程可写成:00.1cos()O y t π?=+
由图形可知:s 31=t 时:0.05O y =,有:00.050.1cos()3
π
?=+
考虑到此时0O
d y d t
<,∴03π?=,
53π(舍去) 那么:(1)O 点的振动表达式:0.1cos()3
O y t π
π=+
;
(2)波动方程为:0.1cos(5)3
y t x π
ππ=-+
;
(3)设A 点的振动表达式为:0.1cos()A A y t π?=+
由图形可知:s 31=
t 时:0A y =,有:cos()03
A π
?+= 考虑到此时0A
d y d t
>,∴56A π?=-
(或76A π?=) ∴A 点的振动表达式:50.1cos()6A y t ππ=-,或70.1cos()6
A y t ππ=+; (4)将A 点的坐标代入波动方程,可得到A 的振动方程为:
0.1cos(5)3
A A y t x π
ππ=-+,与(3)求得的A 点的振动表达式比较,有:
5563A t t x πππππ-=-+,所以:m x A 233.030
7== 。
3-13.一平面简谐波以速度m/s 8.0=u 沿x 轴负方向传播。已知原点的振动曲线如图所示。试写出:
(1)原点的振动表达式; (2)波动表达式;
(3)同一时刻相距m 1的两点之间的位相差。 解:这是一个振动图像!
由图可知A =0.5cm ,设原点处的振动方程为:30510cos()O y t ω?-=?+。 (1)当0t =时,30
2.510O t y -==?,考虑到:
0O t d y d t
=>,有:03
π
?=-
,
当1t =时,10O
t y ==,考虑到:
10O t d y d t
=<,有:3
2
π
π
ω-
=
,56
πω=
, ∴原点的振动表达式:3
5510cos(
)63
O y t ππ-=?-; (2)沿x 轴负方向传播,设波动表达式:3
5510cos()63
y t k x ππ
-=?+- 而512460.825k u ωππ==?=,∴3
524510cos(
)6253
y t x πππ-=?+-; (3)位相差:25
2 3.2724
x k x rad ?ππλ??==?== 。 例题: 例3-1、例3-2、例3-3、例3-4、例3-5
