金融工程实验报告3 根据B-S-M期权定价公式,研究无收益欧式看涨、看跌期权价格随股票价格的变动过程

金融工程实验报告（三）

一、实验名称

根据B-S-M 期权定价公式，研究无收益欧式看涨、看跌期权价格随股票价

格的变动过程。

二、实验目的

在已知布莱克舒尔斯期权定价公式下，通过控制其他变量，如股票年波动率、

无风险利率、看涨看跌期权执行价格以及到期时间对期权价格的影响。研究无收益欧式看涨、看碟期权价格随股票价格的变动过程

三、实验内容

1.实验准备

（1）首先实验需要用到以下公式： B-S-M 无收益欧式看涨期权定价公式：

B-S-M 无收益欧式看跌期权定价公式：

其中：

（2）其他假定条件

在研究无收益欧式看涨、看碟期权价格随股票价格的变动过程，需要空置其他变量固定不变，为了试验结果较好，先控制其他变量数据如下：

)

()(12)(d SN d N Xe p t T r ---=--()12()()

r T t C SN d Xe N d --=-t

T d t T t T r X S d t

T t T r X S d --=---+=--++=σσσσσ12221)

)(2/()/ln())(2/()/ln(

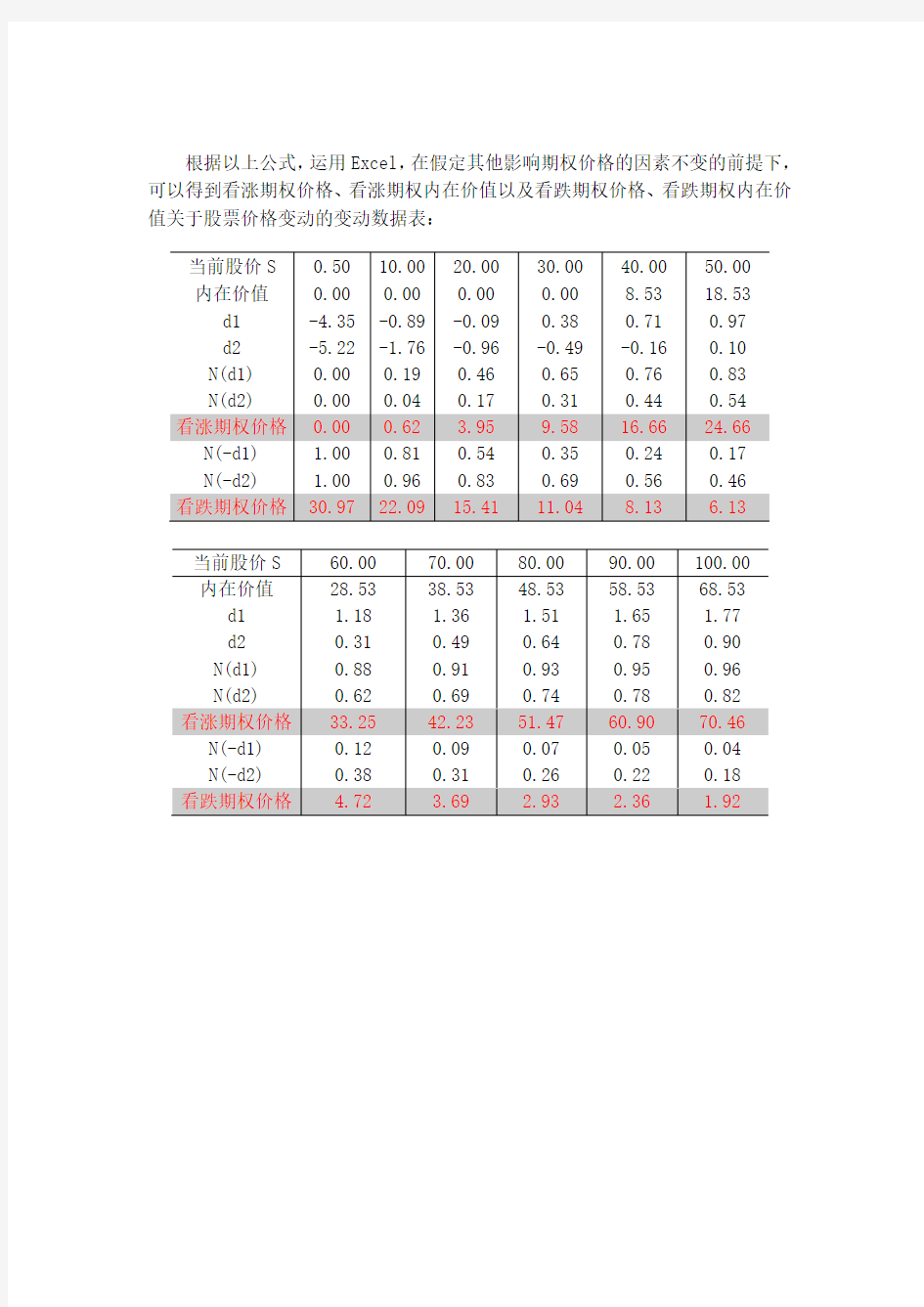
根据以上公式，运用Excel，在假定其他影响期权价格的因素不变的前提下，可以得到看涨期权价格、看涨期权内在价值以及看跌期权价格、看跌期权内在价值关于股票价格变动的变动数据表：

2.无收益欧式看涨期权定价公式

根据以上公式，运用Excel，在假定其他影响期权价格的因素不变的前提下，可以得到看涨期权价格以及看涨期权内在价值关于股票价格变动的变动图

3. 无收益欧式看跌期权定价公式

同样，运用Excel，在假定其他影响期权价格的因素不变的前提下，可以得到看跌期权价格关于股票价格变动的变动图：

四、实验结论

可以得知，在假定其他条件不变的情况下，当当前股票价格大于看涨期权执行价格时，看涨期权执行价格随着骨架市价的增加而成上升趋势，而且执行价格的变化随着市价的上升逐渐增大，同时不断的趋于它的内在价值。而当当前股票价格小于看涨期权执行价格时，它的价格为0，而此时看涨期权的内在价值也为0。

跌期权，同样可以得到，随着市价逐渐下降，即与执行价格差额逐渐增加，看跌期权价格逐渐上升，当股票价格趋近于0时，看跌期权价格趋于看跌期权价格上限，即未来执行价格按照无风险利率的贴现值。

(完整版)期权定价实验报告(E101613109黄冬璇)

广东金融学院实验报告课程名称：金融工程

)t σ T-σ。 t T-

B.实验算例 算例：考虑一个不分红利5个月欧式看涨期权：股票价格为50，执行价格为50，无风险利率为10%，波动率为40。试构造二叉树模型，确定期权的价格。 C.实验过程 在Excel 中创建欧式期权表单模型步骤为（将Excel 求解过程和输出结果截图填写在下面） （1）输入. 在EXCEL 的单元格A4：A9中分别输入“标的资产”、“执行价格”、“波动率”、“到期日”、“无风险利率”和“红利”。其中将期限为5个月的欧式期权的到期日化为单位为年，即为5/12=0.416666667年 ；并且题目中的标的资产的不考虑红利的，所以红利等于0,所以根据题目给出的要求，在对应的单元格B4：B9中分别输入初始值。如下图： 图2-1 欧式看涨期权初始值赋值后的对话框1 （2）欧式看涨期权初始值赋值 假定使用10期的二叉树来计算标的资产的价值，接下来我们可以根据公式t e u ?=σ和t e d ?-=σ来 计算二叉树中的上行和下行的幅度，即u 和d 的值。同时再根据公式d u d e p t r --=?计算其风险中性概率。 利用EXCEL 软件来计算，我们可以先在单元格A14：A16分别输入u 、d 和p 。并在对应的单元格中B14：B16中分别输入公式为“=EXP(B6*SQRT(B7/B12))”，“=1/B14”和“=(EXP(B8*B7/B12)-B15)/(B14-B15)”。得到的结果为u 的值为1.085075596及d 的值为0.921594775，p 的值为0.50513928。计算过程和计算结果如下图：

欧式看涨期权二叉树定价

欧式看涨期权二叉树定价（含m a t l a b代码和结果图）实验概述 本实验首先介绍了二叉树方法的来源和主要理论基础，然后给出期权的二叉树定价方法的基本过程和MATLAB7. 0实现的过程。 19. 2 实验目的 (1)了解二叉树的定价机理; (2)掌握用MATLAB7. 0生成股票价格的二叉树格子方法; (3)掌握欧式期权和美式期权的二叉树定价方法。 19. 3 实验工具 MATLAB 7. 0。 19. 4 理论要点 构造二叉树图(Binomial Tree)是期权定价方法中最为常见的一种。这个树图表示了在期权有效期内股票价格可能遵循的路径。二叉树定价方法与风险中性定价理论是紧密联系的。Cox, Ross & Rubinstein (1979)首次提出了构造离散的风险中性概率可以给期权定价，在此基础上他们给出了二叉树定价方法。 1)一个简单的例子 假设当前(3月份)股票的价格So =50元，月利率是25%。4月份股票价格有两种可能:S高=100元，S低=25元。有一份看涨期权合约，合约约定在4月份可以以50元价格买进一股股票。现在考虑一个投资组合，进行几项操作:以价格C卖出3份看涨期权合约;以50元购入2股股票;以25%的月利率借人40元现金，借期为一个月。 根据上述组合，我们可以得到以下到期收益分布表，如表19. 1所示。 表19.1 投资组合的到期收益分布表 四月份 三月份

S低=25元S高=100元 卖出3份看涨期权合约3C 0 -150 买人两股股票-100 50 200 借人现金40 -50 -50 总计0 0 0 由一价定律3C-100+40=0，可得C= 20元，即为期权的价格。这个例子说明，可以用一个相当简单的方法为期权定价，唯一需要做的是假设对投资者而言不存在套利机会。我们可以通过某种方式构造一个股票和期权的组合，使得在4月份该组合的价值是确定的。于是我们可以说该组合无风险，它的收益率一定等于无风险收益率。二叉树方法正是基于上述思想构造了二项分布下的风险中性概率。 2)二叉树模型 考虑一个不支付红利的股票期权价格估值。我们把期权的有效期分为很多很小的时间间隔Δt。假设在每一个时间段内股票价格从开始的价格S以概率p上升到Su,以概率1-p下降到Sd，其中，u>1,O

金融工程实验报告

金融工程实验报告（一） 布莱克-舒尔斯期权定价模型–基础1.实验目的： 上机操作，利用excel进行与布莱克-舒尔斯期权定价模型有关的分析。 2.实验内容（以看涨期权为例） （1）当前股价与期权价格： 当前股价S（元）看涨期权价格c 80 0.215068699 85 0.653561175 90 1.587638752 95 3.220751797 100 5.65833817 105 8.873031471 110 12.73302365 115 17.06301665 120 21.69844563 125 26.51358001 （2）年波动利率与期权价格： 年波动率 看涨期权价格c 0 0.679096098 0.05 1.814247076 0.1 2.733670055

0.15 3.69937439 0.2 4.676720884 0.25 5.65833817 0.3 6.64163733 0.35 7.625415737 0.4 8.608994221 0.45 9.591927384 （3）无风险利率与期权价格： 无风险利率r 看涨期权价格c 0.47% 5.039542952 5.47% 5.159953019 10.47% 5.282046195 15.47% 5.405814239 20.47% 5.405814239 25.47% 5.65833817 30.47% 5.787073798 35.47% 5.917443799 40.47% 6.04943621 45.47% 6.183038354

（4）协议价格与期权价格： 协议价格X（元）看涨期权价格c 80 21.210864 85 16.56484355 90 12.29478924 95 8.608483995 100 5.65833817 105 3.484203788 110 2.010571467 115 1.089612271 120 0.556432696 125 0.268835874 （5）到期时间与期权价格： 到期时间T-t（年）看涨期权价格c 0.05 2.366046696

林清泉主编的《金融工程》笔记和课后习题详解 第九章 期权定价公式及其应用【圣才出品】

第九章期权定价公式及其应用 9.1复习笔记 一、布莱克一斯科尔斯期权定价公式 1．引言 关于期权定价问题的研究，最早可以追溯到1900年。法国的天才巴彻列尔，在其博士论文中首次给出了初步的欧式买权的定价公式。 20世纪60年代末，布莱克和斯科尔斯得到了描述期权价格变化所满足的偏微分方程，即所谓的B—S方程。1976年，默顿把B—S期权定价模型推广到股票价格变化可能存在跳跃点的场合，并包含了标的股票连续支付股利的情况，从而把该模型的实用性又大大推进了一步，学术界将其称为默顿模型。 2．布莱克一斯科尔斯期权定价公式 （1）基本假设 ①股票价格满足的随机微分方程（9—1）中的μ、σ为常数。 ②股票市场允许卖空。 ③没有交易费用或税收。 ④所有证券都是无限可分的。 ⑤证券在有效期内没有红利支付。 ⑥不存在无风险套利机会。 ⑦交易是连续的。 ⑧无风险利率r为常数。

（2）股票价格的轨道 在通常情况下，假设股票价格S：满足下列随机微分方程： （9—1） （9—2）其中S。称为对数正态过程。 （3）期权套期保值 寻找期权定价公式（函数）的主要思路为：构造以某一种股票和以该股票为标的期权的一个证券组合，而且所构造的证券组合正好是一个无风险资产的复制。 命题9—1设C t=r（t，S t）为期权现价格（t时刻的价格），F（t，z）关于t有一阶连续偏导数，关于x有二阶连续有界偏导数，且满足终值条件： （9—3）则F（t，S）是下列偏微分方程的解： （9—4）为了套期保值此期权，投资者必须卖空r2（t，S）股此股票。反之，若r（t，S）是方程（9—4）的解，则r（t，S t）是满足终值条件h（S T）的自融资证券组合的现值。 （4）布莱克一斯科尔斯公式用（9-5）式解的概率表示： （9—5）定理9—1 ①设S t所满足的方程中的系数均为常数，则期权价格可由下式给出： （9

期权定价

第八章期权定价的二叉树模型 8.1 一步二叉树模型 我们首先通过一个简单的例子介绍二叉树模型。 例8.1 假设一只股票的当前价格是$20，三个月后该股票价格有可能上升到$22，也有可能下降到$18. 股票价格的这种变动过程可通过图8.1直观表示出来。 在上述二叉树中，从左至右的节点（实圆点）表示离散的时间点，由节点产生的分枝（路径）表示可能出现的不同股价。由于从开始至期权到期日只考虑了一个时间步长，图8.1表示的二叉树称为一步（one-step）二叉树。这是最简单的二叉树模型。 一般地，假设一只股票的当前价格是，基于该股票的欧式期权价格为。经过一个时间步（至到期日T）后该股票价 格有可能上升到相应的期权价格为；也有可能下降到相应的期权价格为. 这种过程可通过一步（one-step）二叉树表示出来，如图8.2所示。我们的问题是根据这个二叉树对该欧式股票期权定价。为了对该欧式股票期权定价，我们采用无套利（no arbitrage）假设，即市场上无套利机会存在。构造一个该股票和期权 的组合（portfolio），组合中有股的多头股票和1股空头期权。如果该股票价格上升到，则该组合在期权到期 日的价值为；如果该股票价格下降到，则该组合在期权到期日的价值为。根据无套利假设，该组合在股票上升和下降两种状态下的价值应该相等，即有 由此可得 (8.1) 上式意味着是两个节点之间的期权价格增量与股价增量之比率。在这种情况下，该组合是无风险的。以表示无风险 利率，则该组合的现值（the present value）为,又注意到该组合的当前价值是，故有

即 将(8.1)代入上式，可得基于一步二叉树模型的期权定价公式为 (8.2) (8.3) 需要指出的是，由于我们是在无套利（no arbitrage）假设下讨论欧式股票期权的定价，因此无风险利率应该满足： . 现在回到前面的例子中，假设相应的期权是一个敲定价为$21，到期日为三个月的欧式看涨权，无风险的年利率为12%，求该期权的当前价值。 已知：且在期权到期日， 当时，该看涨权的价值为而当时，该看涨权的价值为 根据(8.3)和(8.2)，可得 . 上述期权定价公式(8.2)和(8.3)似乎与股价上升或下降的概率无关，实际上，在我们推导期权价值时它已经隐含在股票价 格中了。不妨令股价上升的概率为，则股价下降的概率就是，在时间的期望股票价格为

B-S期权定价模型的推导过程

B-S期权定价模型(以下简称B-S模型)及其假设条件 (一)B-S模型有7个重要的假设 1、股票价格行为服从对数正态分布模式； 2、在期权有效期内，无风险利率和金融资产收益变量是恒定的； 3、市场无摩擦，即不存在税收和交易成本，所有证券完全可分割； 4、金融资产在期权有效期内无红利及其它所得(该假设后被放弃)； 5、该期权是欧式期权，即在期权到期前不可实施。 6、不存在无风险套利机会； 7、证券交易是持续的； 8、投资者能够以无风险利率借贷。 (二)荣获诺贝尔经济学奖的B-S定价公式[1] C = S * N(d 1) ? Le? rT N(d2) 其中: C—期权初始合理价格 L—期权交割价格 S—所交易金融资产现价 T—期权有效期 r—连续复利计无风险利率H

σ2—年度化方差 N()—正态分布变量的累积概率分布函数，在此应当说明两点： 第一，该模型中无风险利率必须是连续复利形式。一个简单的或不连续的无风险利率(设为r0)一般是一年复利一次，而r要求利率连续复利。r0必须转化为r方能代入上式计算。两者换算关系为:r = ln(1 + r 0)或r0=Er-1。例如r0=0.06，则r=ln(1+0.06)=0.0583，即100以5.83%的连续复利投资第二年将获106，该结果与直接用r0=0.06计算的答案一致。 第二，期权有效期T的相对数表示，即期权有效天数与一年365天的比值。如果期权有效期为100天，则。 B-S定价模型的推导与运用[1] (一)B-S模型的推导B-S模型的推导是由看涨期权入手的，对于一项看涨期权，其到期的期值是: E[G] = E[max(S t? L,O)] 其中，E[G]—看涨期权到期期望值 S t—到期所交易金融资产的市场价值 L—期权交割(实施)价 到期有两种可能情况: 1、如果S t > L，则期权实施以进帐(In-the-money)生效，且max(S t? L,O) = S t? L 2、如果S t < L，则期权所有人放弃购买权力，期权以出帐(Out-of-the-money)失效，且有: max(S t? L,O) = 0 从而: 其中:P：(S t > L)的概率E[S t | S t > L]：既定(S t > L)下S t的期望值将E[G]按有效期无风险连续复利rT贴现，得期权初始合理价格:

实验5标准欧式看涨期权定价的蒙特卡洛模拟实验报告.doc

陕西科技大学实验报告 课 程： 数理金融 实验日期： 2015 年 6 月 11 日 班 级： 数学122 交报告日期： 2015 年 6 月 12 日 姓 名： 报告退发： （订正、重做） 学 号： 201212010119 教 师： 刘利明 实验名称： 标准欧式看涨期权定价的蒙特卡洛模拟 一、实验预习： 1.标准欧式看涨期权的定价模型。 2.标的资产到期日价格的运动轨迹或分布. 3.蒙特卡洛模拟的过程 二、实验的目的和要求： 通过对标准的欧式期权进行定价模拟，掌握标的资产到期日价格的分布，会熟练运用蒙特卡洛模拟进行期权的定价模拟，并学会分析模拟次数、模拟精度之间的关系，最后和标准的欧式期权的解析解比较给出相对误差。 三、实验过程：（实验步骤、原理和实验数据记录等） 参数：起初（或0时刻）S 取学号后3位除以10取整，然后加上学号最后一位（例如：201212010119，S=[119/10]+9=20）；X 取S 加3；r 取0.03；T 取0.25； σ取0.5。(模拟100次取最后结果平均值) 注意：实验为标准的欧式看涨期权。 实验步骤、原理 蒙特卡罗模拟进行期权定价的核心在于生成股票价格的随机过程。模型假定在期权到期的T 时刻。 标的股票价格的随机方程为： 其中，随机变量ε服从标准正态分布，即服从N(0,1)，随机变量YT 服从正态分布，其均值为()T u u T 25.0σ-=，方差为T T σσ=，u 为股票的收益率，σ为股票的波动率。期权的收益依赖于ST 在风险中性世界里的期望值，因此对于风险中性定价，股票的收益率u 可以用无风险利率r 减去连续红利收益率q 代替，也就是（r-q ）。 风险中性定价的随机方程为：()[] T T q r S S T εσσ+--=25.0ex p 其中ε服从标准正态分布。 成绩 ()() T T T T u S Y S S εσ+==ex p ex p

欧式看涨期权二叉树定价

欧式看涨期权二叉树定价（含ｍａｔlab代码和结果 图) 实验概述 本实验首先介绍了二叉树方法的来源和主要理论基础,然后给出期权的二叉树定价方法的基本过程和MAＴLAB7.0实现的过程。 19. 2 实验目的 （1)了解二叉树的定价机理; (2）掌握用MＡTLAB７. ０生成股票价格的二叉树格子方法; (3）掌握欧式期权和美式期权的二叉树定价方法。 19．３实验工具 ＭＡTLAＢ7. ０。 19. 4理论要点 构造二叉树图(Biｎｏmial Tree）是期权定价方法中最为常见的一种。这个树图表示了在期权有效期内股票价格可能遵循的路径。二叉树定价方法与风险中性定价理论是紧密联系的。Cox,Rosｓ＆Ｒubｉnstein（19７9)首次提出了构造离散的风险中性概率可以给期权定价,在此基础上他们给出了二叉树定价方法。 1)一个简单的例子 假设当前（３月份)股票的价格So =50元，月利率是25%。4月份股票 价格有两种可能:S 高=10０元,S 低 =25元。有一份看涨期权合约,合约约定在4月份

可以以50元价格买进一股股票。现在考虑一个投资组合,进行几项操作：以价格C卖出3份看涨期权合约;以50元购入２股股票;以２5%的月利率借人40元现金，借期为一个月。 根据上述组合，我们可以得到以下到期收益分布表，如表19.1所示。 表１9.1投资组合的到期收益分布表 四月份 三月份 =25元 S 低=100元 Ｓ 高 卖出3份看涨期权合约3C 0 －150 买人两股股票-10０50 200 借人现金40 -50 －5０ 总计0 ０0 由一价定律３Ｃ-10０+40=0,可得C=20元，即为期权的价格。这个例子说明,可以用一个相当简单的方法为期权定价，唯一需要做的是假设对投资者而言不存在套利机会。我们可以通过某种方式构造一个股票和期权的组合，使得在4月份该组合的价值是确定的。于是我们可以说该组合无风险,它的收益率一定等于无风险收益率。二叉树方法正是基于上述思想构造了二项分布下的风险中性概率。 ２)二叉树模型 考虑一个不支付红利的股票期权价格估值。我们把期权的有效期分为很多很小的时间间隔Δt。假设在每一个时间段内股票价格从开始的价格S以概率p 上升到Su,以概率1-p下降到Ｓd,其中,u>1,Ｏ

B-S期权定价公式

Black-Scholes 期权定价模型 一、Black-Scholes 期权定价模型的假设条件 Black-Scholes 期权定价模型的七个假设条件如下: 1、 风险资产(Black-Scholes 期权定价模型中为股票),当前时刻市场价格为S 。S 遵循几何布朗运动,即dz dt S dS σμ+=。 其中,dz 为均值为零,方差为dt 的无穷小的随机变化值(dt dz ε=,称为标准布朗运动,ε代表从标准正态分布(即均值为0、标准差为1的正态分布)中取的一个随机值),μ为股票价格在单位时间内的期望收益率,σ则就是股票价格的波动率,即证券收益率在单位时间内的标准差。μ与σ都就是已知的。 简单地分析几何布朗运动,意味着股票价格在短时期内的变动(即收益)来源于两个方面:一就是单位时间内已知的一个收益率变化μ,被称为漂移项,可以被瞧成一个总体的变化趋势;二就是随机波动项,即dz σ,可以瞧作随机波动使得股票价格变动偏离总体趋势的部分。 2.没有交易费用与税收,不考虑保证金问题,即不存在影响收益的任何外部因素。 3、 资产价格的变动就是连续而均匀的,不存在突然的跳跃。 4、 该标的资产可以被自由地买卖,即允许卖空,且所有证券都就是完全可分的。 5、 在期权有效期内,无风险利率r 保持不变,投资者可以此利率无限制地进行借贷。 6.在衍生品有效期间,股票不支付股利。 7.所有无风险套利机会均被消除。 二、Black-Scholes 期权定价模型 (一)B-S 期权定价公式 在上述假设条件的基础上,Black 与Scholes 得到了如下适用于无收益资产

欧式瞧涨期权的Black-Schole 微分方程: rf S f S S f rS t f =??+??+??2 22221σ 其中f 为期权价格,其她参数符号的意义同前。 通过这个微分方程,Black 与Scholes 得到了如下适用于无收益资产欧式瞧涨期权的定价公式:)()(2)(1d N Xe d SN c t T r ---= 其中, t T d t T t T r X S d t T t T r X S d --=---+=--++=σσσσσ12221))(2/()/ln() )(2/()/ln( c 为无收益资产欧式瞧涨期权价格;N(x)为标准正态分布变量的累计概率分布函数(即这个变量小于x 的概率),根据标准正态分布函数特性,我们有)(1)(x N x N -=-。 (二)Black-Scholes 期权定价公式的理解 1、 1()SN d 可瞧作证券或无价值瞧涨期权的多头;()2()r T t Ke N d --可瞧作K 份现金或无价值瞧涨期权的多头。 可以证明,1/()f S N d ??=。为构造一份欧式瞧涨期权,需持有1()N d 份证券多头,以及卖空数量为2 ()rT K e N d -的现金。 Black-Scholes 期权定价公式用于不支付股利的欧式瞧涨期权的定价。 注意: 该公式只在一定的假设条件下成立,如市场完美(无税、无交易成本、资产无限可分、允许卖空)、无风险利率保持不变、股价遵循几何布朗运动等。 2、风险中性定价原理 风险中性定价原理:我们可以注意到期权价格就是与标的资产的预期收益率无关的。C(S, t)与 S 、r 、t 、T 、σ以及 K 有关,而与股票的期望收益率μ无关。这说明欧式Call 的价格与投资者的风险偏好无关。 在对欧式Call 定价时,可假设投资者就是风险中性的(对所承担的风险不要求额外回报,所有证券的期望收益率等于无风险利率)。

期权定价实验报告M101613110黄清霞

阅读使人充实，会谈使人敏捷，写作使人精确。——培根广东金融学院实验报告 课程名称：金融工程

法拉兹·日·阿卜——学问是异常珍贵的东西，从任何源泉吸收都不可耻。．阅读使人充实，会谈使人敏捷，写作使人精确。——培根

阅读使人充实，会谈使人敏捷，写作使人精确。——培根

法拉兹·日·阿卜——学问是异常珍贵的东西，从任何源泉吸收都不可耻。． 阅读使人充实，会谈使人敏捷，写作使人精确。——培根 MATLA中的计算过程和结果如下（请将运算过程和结果粘贴下面1二叉树定价函数确定期权价 >> [AssetPrice,OptionValue]=binprice(50,50,0.1,5/12,1/12,0.4,1) AssetPrice = 50.0000 56.1200 62.9892 70.6991 79.3528 89.0656 0 44.5474 50.0000 56.1200 62.9892 70.6991 0 0 39.6894 44.5474 50.0000 56.1200 0 0 0 35.3611 39.6894 44.5474 0 0 0 0 31.5049 35.3611 0 0 0 0 0 28.0692 OptionValue = 6.3595 9.8734 14.8597 21.5256 29.7677 39.0656 0 2.8493 4.9066 8.2481 13.4041 20.6991 0 0 0.7794 1.5491 3.0791 6.1200 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2求解公式确定期权价 p =q = d =a =u = 0.50731.00840.4927 1.12240.8909 BinTree = 50.0000 56.1200 62.9892 70.6991 79.3528 89.0656 0 44.5474 50.0000 56.1200 62.9892 70.6991 0 0 39.6894 44.5474 50.0000 56.1200 0 0 0 35.3611 39.6894 44.5474 0 0 0 0 31.5049 35.3611 0 0 0 0 0 28.0692 BinPrice = 6.3595 9.8734 14.8597 21.5256 29.7677 39.0656 0 2.8493 4.9066 8.2481 13.4041 20.6991 0 0 0.7794 1.5491 3.0791 6.1200 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

金融工程-二叉树模型——期权定价方法试验报告---用于合并

期权定价（二叉树模型）实验报告1204200308 学号：1201 姓 名：郑琪瑶班级：创金 一、实验目的计算出支付连续红利率资产Excel 本实验基于二叉树模型对 期权定价。利用的期权价格，并探究输入参数（如无风险利率、波动率、期限、时间区间划分方从而巩固二叉树模型这种期权定价的数对于期权价格的影响，式、收益率等等）值方法的相关知识。 二、实验原理的红利时，在风险中性条件下，证券价格的当标的资产支付连续收益率为q应该满足以下，因此参数（股票价格上升的概率）、、增长率应该为pq?r u d式子：tq)?(r?dpe)(?pu?1?；同时在一小段时间内股票价格变化的方差 满足下式：2222?]p1?)p)dd?[pu?(?t?pu?(1?；1，将三式联列，可以解考克斯、罗斯和鲁宾斯确定参数的第三个条件是?u d）得（*(r?q)?t??edp?? u?d????t u?e????t?d?e???t?0?三、实验内容 1.假定有一支付连续红利率股票的美式看涨期权，有效期期限为5个月，目前 的股票价格和期权执行价格都为50元，无风险利率为10%，波动率为40%，连续收益率为3%，为了使得估计的期权价格比较准确，把时间区间划分成30步，即N=30，利用excel加载宏可以计算得到相应美式和欧式期权的价格 2.探究基于不同红利支付类型：支付已知收益率和支付已知红利数额，计算出相应的美式和欧式期权价格。 3.以支付已知收益率模式下分析期权价格。使资产连续复利收益率在[1%,10%]变化，保持其余变量不变，分别计算出相应美式f和欧式f期权的价格21 4.以支付已知红利数额模式下分析期权价格。探究下一期的红利支付数额为常数、递增及递减情况下，保持其余变量不变，分别计算出相应美式和欧式期权的价格。 5.根据上述每一步计算得到的当期期权价格的数据绘制折线图，观察折线图，得出结论。 四、实验过程：步骤一：输入已知参数输入参数支付连续收TRSX N 步数无风险利率波动率σ股票价格期限期权执行价格0RC益率9.00% 5 50.00

期权定价模型

期权定价模型 什么是期权 期权，又称为选择权，指一种能在未来某特定时间以特定价格买入或卖出一定数量的某种特定商品的权利。它是在期货的基础上产生的一种金融工具，给予买方（或持有者）购买或出售标的资产的权利。期权的持有者可以在该项期权规定的时间内选择买或不买、卖或不卖的权利，他可以实施该权利，也可以放弃该权利，而期权的出卖者则只负有期权合约规定的义务。 Black-Scholes 期权定价模型 股票价格的变动一般没有规律可循，但我们可以用随机过程来刻画股价的变动过程。特别的，我们可以假设股价遵循几何维纳过程。1973年，斯坦福大学的教授Myron Scholes 和他的同事、已故数学家Fischer Black 在美国《政治经济学》上发表了论文《期权与公司债务的定价》，给出了欧式看涨期权的定价公式，即著名的Black-Scholes 期权定价模型。该模型被称为“不仅在金融领域，而且在整个经济学中最成功的理论”。在模型的应用、改进和扩展方面，哈佛商学院的教授Merton 也做了大量的研究工作。因此，Scholes 和Merton 被授予1997年的诺贝尔经济学奖，以表彰他们所做出的杰出贡献。 二叉树期权定价模型 虽然Black-Scholes 期权定价模型有许多优点，但是它复杂的数学推导和求解过程在金融界较难被广泛接受和掌握。1979年，J.C.Cox 、S.A.Ross 和M.Rubinstein 在《金融经济学杂志》上发表论文《期权定价：一种简单的方法》，提出了一种比较浅显的期权定价方法，被称为Cox-Ross-Rubinstein 二项式期权定价模型（Binomial Model ）或二叉树期权定价模型（Binomial tree ）。二叉树期权定价模型建立在一个基本假设基础上，即在给定的时间间隔内，证券的价格运动有两个可能的方向：上涨或者下跌。 窝轮的定价及影响因素 目前香港的窝轮发行商给窝轮定价时基本上都是采用Black-Scholes 期权定价模型。所不同的是，各个发行商对模型中的参数如无风险利率，红利和波动率的选取都有所不同。比如发行商会考虑自身的资产状况和借贷资金成本来界定无风险利率，对公司红利的派发预期也有所不同，另外对波动率的选取和稳定性维护更是能体现发行商的信誉和资质水平。 牛熊证的定价及影响因素 牛熊证作为一种新型结构性产品于2006年6月被引入香港市场之后，发展至今深受市场欢迎。由于牛熊证设有收回价机制，在定价方面，牛熊证和窝轮完全不同。用数学公式表示，即为： ()E r T X X S c ??+?=)(，()E r T S S X p ??+?=)( 其中p c 、分别为牛证和熊证的价格，E r T X S 、、、、分别为正股股价、行使价、剩余期限、年息和兑换比率。 招商证券（香港）研究部 陈文质 (86-755) 83295367 cwz@https://www.wendangku.net/doc/4519119405.html, 何 钟 (852) 31896818 hezhong@https://www.wendangku.net/doc/4519119405.html, 2009年4月2日

期权定价的数值方法

期权定价的数值方法 小结 1.当不存在解析解时，可以用不同的数值方法为期权定价，其中主要包括二叉树图方法、蒙特卡罗模拟和有限差分方法。 2.二叉树图方法用离散的随机游走模型模拟资产价格的连续运动在风险中性世界中可能遵循的路径，每个小的时间间隔中的上升下降概率和幅度均满足风险中性原理。从二叉树图的末端开始倒推可以计算出期权价格。 3.蒙特卡罗方法的实质是模拟标的资产价格在风险中性世界中的随机运动，预测期权的平均回报，并由此得到期权价格的一个概率解。 4.有限差分方法将标的变量满足的偏微分方程转化成差分方程来求解，具体的方法包括隐性有限差分法、显性有限差分法、“跳格子方法”和 Crank-Nicolson方法等。 5.树图方法和有限差分方法在概念上是相当类似的，它们都可以看成用离散化过程解出偏微分方程的数值方法，都适用于具有提前执行特征的期权，不太适合路径依赖型的期权。其中二叉树模型由于其简单直观和容易实现，是金融界中应用得最广泛的数值定价方法之一；有限差分方法则日益受到人们的重视。 6.蒙特卡罗方法的优点在于应用起来相当直接，能处理许多盈亏状态很复杂的情况，尤其是路径依赖期权和标的变量超过三个的期权，但是不擅长于处理美式期权，而且往往所需计算时间较长。 二叉树定价方法的基本思想：假设资产价格的运动是由大量的小幅度二值运动构成，用离散的随机游走模型模拟资产价格连续运行可能遵循的路径。模型中隐含导出的概率是风险中性世界中的概率p，从而为期权定价。 蒙特卡洛模拟的基本思想：由于大部分期权的价值都可以归结为期权到期回报的期望值的贴现，因此尽可能地模拟风险中性世界中标的资产价格的多种运动路径，计算每种结果路径下的期权回报均值，之后贴现就可以得到期权价值。 蒙特卡洛模拟的优点：在大多数情况下，人们可以很直接地应用蒙特卡洛模拟，而无需对期权定价模型有深刻的认识；蒙特卡洛模拟的适用情形相当广泛。 蒙特卡洛模拟的缺点：只能为欧式期权定价，难以处理提前执行期权的的定价情形；为了达到一定的精准度，需要大量的模拟运算。 有限差分方法的基本思想：将衍生证券所满足的偏微分方程转化为一系列近似的差分方程，即用离散算子逼近偏微分方程中的各项，之后用迭代法求解以得到期权价值。

第七章美式期权定价金融衍生品定价理论讲义

第七章 美式期权定价 由于美式期权提前执行的可能，使得解决最优执行决策成为美式期权定价和套期保值的关键。由第三章的内容我们知道，如果标的股票在期权的到期日之前不分红，则美式看涨期权不会提前执行，因为在到期日之前执行将损失执行价格的利息。但是，如果标的股票在期权到期日以前支付红利，则提前执行美式看涨期权可能是最优的。提前执行可以获得股票支付的红利，而红利的收入超过利息损失。事实上，我们将证明，投资者总是在股票分红前执行美式看涨期权。 对于美式看跌期权而言，问题变的更复杂。看跌期权的支付以执行价格为上界，这限制了等待的价值，所以对于美式看跌期权而言，即使标的股票不支付红利，也可能提前执行。提前执行可以获得执行价格的利息收入。 许多金融证券都暗含着美式期权的特性，例如可回购债券（called bond ），可转换债券（convertible bond ）， 假设： 1．市场无摩擦 2．无违约风险 3．竞争的市场 4．无套利机会 1．带息价格和除息价格 每股股票在时间t 支付红利t d 元。当股票支付红利后，我们假设股价将下降，下降 的规模为红利的大小。可以证明，当市场无套利且在资本收益和红利收入之间没有税收差别时，这个假设是成立的。 ()()t e c d t S t S += 这里()t S c 表示股票在时间t 的带息价格，()t S e 表示股票在时间t 的除息价格。 这个假设的证明是非常直接的。如果上述关系不成立，即()()t e c d t S t S +≠，则存在套利机会。 首先，如果()()t e c d t S t S +>，则以带息价格卖出股票，在股票分红后马上以除息 价格买回股票。因为我们卖空股票，所以红利由卖空者支付，从而这个策略的利润为 ()()()t e c d t S t S +-。因为红利是确定知道的，所以只要()()() t S t S e c -var =0，则利润是 没有风险的。 其次，如果()()t e c d t S t S +<，则以带息价格买入股票，获得红利后以除息价格卖 出，获得利润为()()t S d t S c t e -+。

(实验5)标准欧式看涨期权定价的蒙特卡洛模拟实验报告

课程：数理金融实验日期：2013 年 5 月21 日班级：数学102 交报告日期：2013 年 5 月23 日姓名：张瑞琪报告退发：（订正、重做）学号：201012010213 教师：刘利明 实验名称：标准欧式看涨期权定价的蒙特卡洛模拟 一、实验预习： 1.标准欧式看涨期权的定价模型。 2.标的资产到期日价格的运动轨迹或分布. 3.蒙特卡洛模拟的过程 二、实验的目的和要求： 通过对标准的欧式期权进行定价模拟，掌握标的资产到期日价格的分布，会熟练运用蒙特卡洛模拟进行期权的定价模拟，并学会分析模拟次数、模拟精度之间的关系，最后和标准的欧式期权的解析解比较给出相对误差。 三、实验过程：（实验步骤、原理和实验数据记录等） 参数：起初（或0时刻）S取学号后3位除以10取整，然后加上学号最后一位（例如：200912010119，S=[119/10]+9=20）；X取S加3；r取0.03；T取0.25；σ取0.5。 注意：实验为标准的欧式看涨期权。 实验原理 1.标准欧式看涨期权的定价模型。 (1)看涨期权价格的上限。在任何情况下，期权的价值都不会超过标的资产的价格。否则的话，套利者就可以通过买入标的资产并卖出期权来获取无风险利润。 c S c代表欧式看涨期权价格，S代表标的资产价格 （2）)看涨期权价格的下限。 2.标的资产到期日价格的运动轨迹或分布. 3.蒙特卡洛模拟的过程 蒙特卡洛模拟（Monte Carlo simulation）：计算机仿真 蒙特卡洛模拟也是一种非参数方法，其计算原理与历史模拟法相同，都是通过模 拟资产回报的得到各种可能结果，并由此计算VaR。

陕西科技大学理学院实验报告 与历史模拟不同的是：蒙特卡洛模拟法对资产价格分布的估计不是来自历史的观测值，而是通过产生大量的随机数得到的。 蒙特卡洛模拟法的本质：把所有的可能列出（枚举法）。 基本步骤 1情景产生：通过产生服从某种分布的随机数，构造可能情景（比如东南亚金融危机）。 2资产估值：在每个情景下计算资产的价格。 3估计VaR ：根据资产价格分布，计算某个置信水平下的VaR 。 S=[213/10]+3=24 ,X=S+3=27 ,r=0.03 ,T=0.25 , σ=0.5 四、实验总结：（实验数据处理和实验结果讨论等） 实验数据处理 1.标准的欧式期权定价（风险中性定价）： 当t ?很小时：T t =? d u d e p t r --=? （8.4） t e u ?=σ （8.5） t e d ?-=σ （8.6） ) 0,*max()0,*max(X s d f X s u f d u -=-= 从而 ()1r t u d f e pf p f -?=+-???? 带入 25.0=?t ，S=24，X=27，r=0.03,T=0.25,σ=0.5 得期权价格为：f =1.7150 程序代码： b=0.5,r=0.03,T=0.25,s=24,x=27; u=exp(b*sqrt(T)); d=exp(-(b*sqrt(T))); p=(exp(r*T)-d)/(u-d); f1=max(u*s-x,0); f2=max(d*s-x,0); f=exp(-(r*T))*(p*f1+(1-p)*f2) 2.蒙特卡洛模拟的过程(1000次模拟): Price =1.7570 程序代码：

欧式期权二叉树定价MATLAB代码

调用函数代码 function Price=EuroOption(S0,K,T,r,M,type,sigma) dt = T/M; u=exp(sqrt(dt)*sigma); d=1/u; p = (exp(r*dt)-d)/(u-d); S=zeros(M+1,M+1); S(1,1)=S0; for j=1:M for i=0:j S(i+1,j+1)= S0*u^(j-i)*d^i; end end V=zeros(M+1,M+1); for i=0:M switch type case'call' V(i+1,M+1)=max(S(i+1,M+1)-K,0); case'put' V(i+1,M+1)=max(K-S(i+1,M+1),0); case'stra' V(i+1,M+1)=max(S(i+1,M+1)-K,0)+max(K-S(i+1,M +1),0); case'bino' V(i+1,M+1) =(S(i+1,M+1)>K); end end

for j=M-1:-1:0 for i=0:j V(i+1,j+1)=exp(-r*dt)*(p*V(i+1,j+2)+(1-p)*V( i+2,j+2)); end end Price=V(1,1); 数据作图 S0 = 6; K = 5; T = 1; r = 0.05; sigma = 0.20; for M=1:100 type='call'; Price=EuroOption(S0,K,T,r,M,type,sigma); Vec(M)=Price; end for M=1:100 type='put'; Price=EuroOption(S0,K,T,r,M,type,sigma); Vep(M)=Price; end for M=1:100 type='call'; Price=AmOption(S0,K,T,r,M,type,sigma); Vac(M)=Price; end for M=1:100 type= 'put'; Price=AmOption(S0,K,T,r,M,type,sigma);

第八章--蒙特卡洛期权定价方法

第八章蒙特卡洛期权定价方法 在金融计算中蒙特卡洛模拟是一种重要的工具：可以用来评估投资组合管理规则、为期权定价、模拟套期保值交易策略、估计风险价值。蒙特卡洛方法主要的优势在于对大多数情况都适用、易于使用、灵活。它把随机波动性和奇异期权的很多复杂特性都考虑进去了，更倾向于使用处理高维问题，而网格和PDF分析框架却不适用。蒙特卡洛模拟潜在的劣势在于它的计算量大。多次的重复需要完善我们所关注的置信区间的估计。利用方差缩减技术和低差异序列可以部分的解决这个问题。本章的目的是解释这些技术在一些例子上的应用，包括一些路径依赖型期权。这章是第四章的延伸，在第四章里我们讨论了蒙特卡洛积分。需要强调的是蒙特卡洛方法是概念上的一个数字积分工具，即使我们适用更多的“模拟”或“抽样”。在使用低差异序列而不是伪随机生成时这需要牢记。 如果可能，我们可以把模拟的结果和分析公式进行比较。很明显我们这样做的目标是一个纯粹的教学。如果你要计算一个矩形房间的面积，你只需要用房间的长度乘以房间的宽度即可，而不必要计算有多少次一块标准砖与这个表面相匹配。尽管如此，你还是应该学会在一些简单案例中首先适用模拟的方法，在这些简单的例子中我们可以检验答案的一致性；更进一步，我们也要看为达到方差减小的目的分析公式可用于的模拟期权可能更有力的控制变量。 蒙特卡洛应用的出发点是生成样本路径，这个生成的样本路径给予一个描述价格（或利率）动态的随机微分方程。在8.1节我们解释几何布朗运动的路径生成；

在一个具体例子中模拟两个对冲策略，我们也会讨论布朗桥，它是适时推进模拟样本的一个替代方案。在8.2节将讨论交换期权，它被用作为一个如何将这种方法推广到多维过程的一个简单实例。在8.3节我们考虑一个弱路径依赖型期权的例子，这是个下跌敲出看跌期权；我们加入了有条件的蒙特卡洛和为减小方差抽样的重要性。在8.4节将讨论到强路径依赖型期权，同时我们证明了运用控制变量和低差异序列为算术平均亚式期权定价。我们以概述由蒙特卡洛抽样产生的估计期权敏感性的基本问题来结束本章；在8.5节我们考虑一个普通的看涨期权A的简单案例。在第10.4节将讨论到随机模拟期权定价的另一个应用，它应用于美式期权；而一个简单的模拟方法在早期的应用中不可实行，并且这个问题在随机动态优化的框架里被强制转换。 8.1 路径生成 蒙特卡洛期权定价方法的应用的出发点是对样本基本因素路径的产生。对于一般的期权就像在第四章里面一样不需要产生路径：只需要关注标的资产到期日的价格。但是如果路径依赖型期权，我们就需要整条路径或者至少需要在给定时刻的一系列价值。如果服从几何布朗运动，情况的处理就非常简单。事实上，必须认识到在路径生成中有两个误差源：样本误差、离散误差。 样本错误时因为蒙特卡洛方法的随机性，这个问题可以通过减小方差的办法得到缓解。为了理解什么是离散错误，我们考虑一个典型的离散连续时间模型，例如：伊藤随机微分方程：

5蒙特卡洛方法模拟期权定价

材料五：蒙特卡洛方法模拟期权定价 1．蒙特卡洛方法模拟欧式期权定价 利用风险中性的方法计算期权定价： ?()rt T f e E f -= 其中，f 是期权价格，T f 是到期日T 的现金流，?E 是风险中性测度 如果标的资产服从几何布朗运动： dS Sdt sdW μσ=+ 则在风险中性测度下，标的资产运动方程为： 2 0exp[()]2T S S r T σ=-+ 对于欧式看涨期权，到期日欧式看涨期权现金流如下： 2 (/2)max{0,(0)}r T S e K σ-+- 其中，K 是执行价，r 是无风险利率，σ是标准差， ε是正态分布的随机变量。 对到期日的现金流用无风险利率贴现，就可知道期权价格。 例1 假设股票价格服从几何布朗运动，股票现在价格为50，欧式期权执行价格为52，无风险利率为0.1，股票波动标准差为0.4，期权的到期日为5个月，试用蒙特卡洛模拟方法计算该期权价格。 下面用MATLAB 编写一个子程序进行计算： function eucall=blsmc(s0,K,r,T,sigma,Nu) %蒙特卡洛方法计算欧式看涨期权的价格 %输入参数 %s0 股票价格 %K 执行价 %r 无风险利率 %T 期权的到期日 %sigma 股票波动标准差 %Nu 模拟的次数 %输出参数 %eucall 欧式看涨期权价格 %varprice 模拟期权价格的方差 %ci 95%概率保证的期权价格区间

randn('seed',0); %定义随机数发生器种子是0, %这样保证每次模拟的结果相同 nuT=(r-0.5*sigma^2)*T sit=sigma*sqrt(T) discpayoff=exp(-r*T)*max(0,s0*exp(nuT+sit*randn(Nu,1))-K) %期权到期时的现金流 [eucall,varprice,ci]=normfit(discpayoff) %在命令窗口输入：blsmc(50,52,0.1,12/5,0.4,1000) 2． 蒙特卡洛方法模拟障碍期权定价 障碍期权，就是确定一个障碍值b S ，在期权的存续期有可能超过该价格，也可能低于该价格，对于敲出期权而言，如果在期权的存续期标的资产价格触及障碍值时，期权合同可以提前终止执行；相反，对于敲入价格，如果标的资产价格触及障碍值时，期权合同开始生效。 当障碍值b S 高于现在资产价格0S ，称上涨期权，反之称下跌期权。 对于下跌敲出看跌期权，该期权首先是看跌期权，股票价格是0S ，执行价格是K ，买入看跌期权就首先保证以执行价K 卖掉股票，下跌敲出障碍期权相当于在看跌期权的基础上附加提前终止执行的条款，容是当股票价格触及障碍值b S 时看跌期权就提前终止执行。因为该期权对于卖方有利，所以其价格应低于看跌期权的价格。 对于下跌敲出看跌期权，该期权首先是看跌期权，股票价格是0S ，执行价格是K ，买入看跌期权就首先保证以执行价K 卖掉股票，下跌敲出障碍期权相当于在看跌期权的基础上附加提前终止执行的条款，容是当股票价格触及障碍值b S 时看跌期权就提前终止执行。因为该期权对于卖方有利，所以其价格应低于看跌期权的价格。 对于下跌敲入看跌期权，该期权首先是看跌期权，下跌敲出障碍期权相当于在看跌期权的基础上附加提前何时生效的条款，容是当股票价格触及障碍值b S 时看跌期权开始生效。 当障碍值b S 确定时，障碍期权存在解： 4275{()()[()()]}rT P Ke N d N d a N d N d -=--- 03186{()()[()()]}S N d N d b N d N d ---- 其中 212/0()r b S a S σ-+=， 212/0 ()r b S b S σ+=， 2 1d =