互相关延时估计加权函数性能分析报告

互相关延时估计加权函数性能分析

广义互相关函数法是通过首先求出俩信号之间的互功率谱，然后在频域内给予一定的加权，以此对信号和噪音进行白化处理，从而增强信号中信噪比较高的频率成分，抑制噪声的影响，最后再反变换到时域，得到两信号之间的互相关函数，即：

?=π

τψτ0121212)()()(dw e w G w R jw （1） 其中)(12w ψ是广义互相关加权函数。广义互相关加权函数的选择主要基于俩个方面：噪声和反射情况。根据不同的情况选择加权函数，其目的就是使)(12τR 具有比较尖锐的峰值。)(12τR 峰值处就是俩个传感器之间的时延。

由于来自同一声源的信号存在一定的相关性，通过计算不同麦克风所接受到的信号之间的相关函数，就可以估计出TDOA 值。然而在实际环境中，由于噪声和混响的影响，相关函数的最大峰会被弱化，有时还会出现多个峰值，这些都造成了实际峰值的检测困难。此时就通过加权的方法来锐化峰值，通常我们通过时间、精度来确定算法的合理性。

一、 广义互相关函数模拟

clear all; clc; close all;

N=1024; %长度

Fs=500; %采样频率

n=0:N-1;

t=n/Fs; %时间序列

a1=5; %信号幅度

a2=5;

d=2; %延迟点数

x1=a1*cos(2*pi*10*n/Fs); %信号1

x1=x1+randn(size(x1)); %加噪声

x2=a2*cos(2*pi*10*(n+d)/Fs); %信号2

x2=x2+randn(size(x2));

subplot(211);

plot(t,x1,'r');

axis([-0.2 1.5 -6 6]);

hold on;

plot(t,x2,':');

axis([-0.2 1.5 -6 6]);

legend('x1信号', 'x2信号');

xlabel('时间/s');ylabel('x1(t) x2(t)');

title('原始信号');grid on;

hold off

%互相关函数

X1=fft(x1,2*N-1);

X2=fft(x2,2*N-1);

Sxy=X1.*conj(X2);

Cxy=fftshift(ifft(Sxy));

%Cxy=fftshift(real(ifft(Sxy)));

subplot(212);

t1=(0:2*N-2)/Fs; %注意

plot(t1,Cxy,'b');

title('互相关函数');xlabel('时间/s');ylabel('Rx1x2(t)');grid on [max,location]=max(Cxy);%求出最大值max,及最大值所在的位置（第几行）location;

%d=location-N/2-1 %算出延迟了几个点

d=location-N

Delay=d/Fs %求得时间延迟

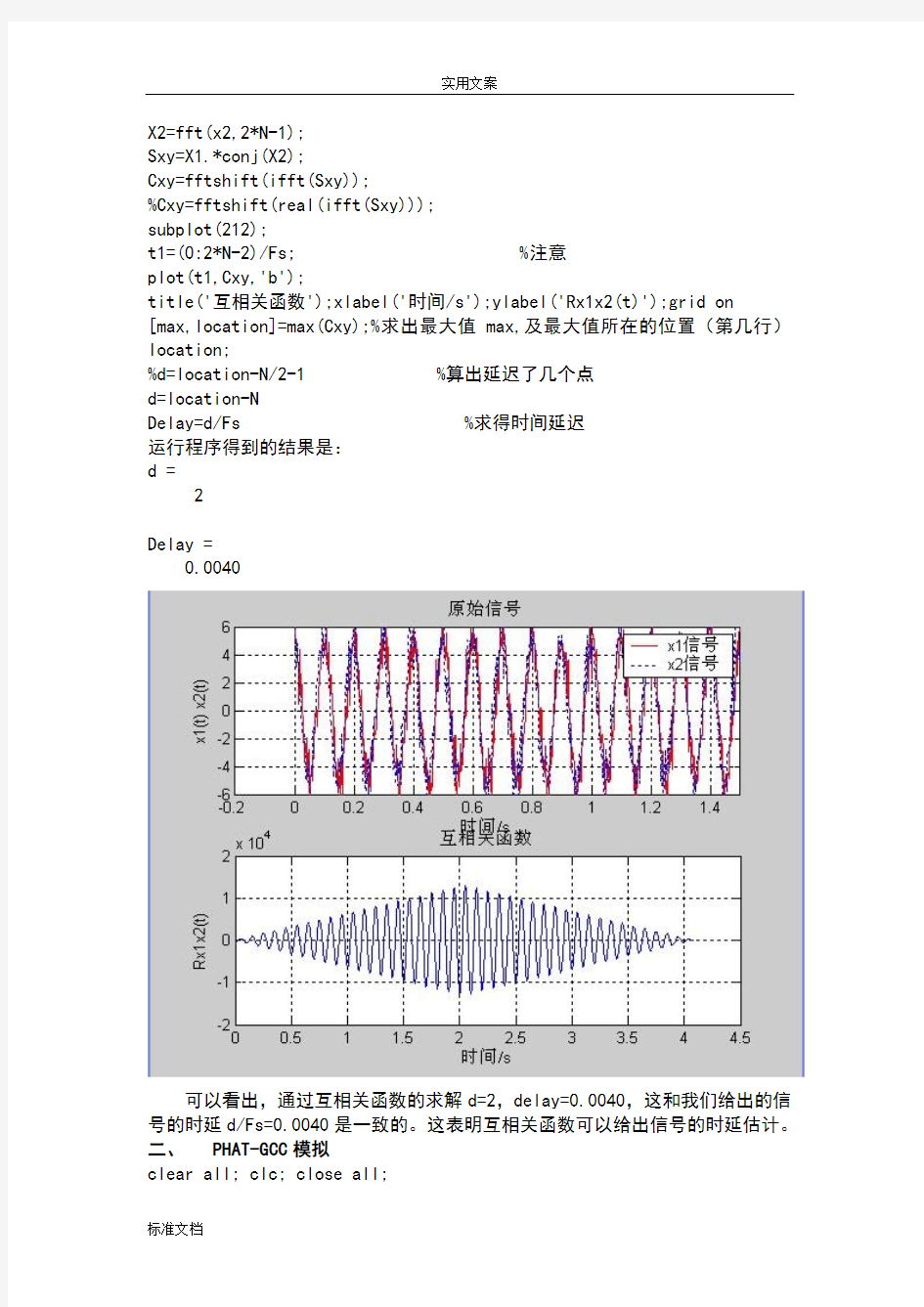
运行程序得到的结果是：

d =

2

Delay =

0.0040

可以看出，通过互相关函数的求解d=2，delay=0.0040，这和我们给出的信号的时延d/Fs=0.0040是一致的。这表明互相关函数可以给出信号的时延估计。

二、PHAT-GCC模拟

clear all; clc; close all;

N=1024; %长度

Fs=500; %采样频率

n=0:N-1;

t=n/Fs; %时间序列

a1=5; %信号幅度

a2=5;

d=9; %延迟点数

x1=a1*cos(2*pi*10*n/Fs); %信号1

x1=x1+randn(size(x1)); %加噪声

%x1=x1.*hamming(max(size(x1)))';%加窗

x2=a2*cos(2*pi*10*(n+d)/Fs); %信号2

x2=x2+randn(size(x2));

%x2=x2.*hamming(max(size(x2)))';%加窗

subplot(211);

plot(t,x1,'r');

axis([-0.2 2 -6 6]);

hold on;

plot(t,x2,':');

axis([-0.2 2 -6 6]);

legend('x1信号', 'x2信号');

xlabel('时间/s');ylabel('x1(t) x2(t)');

title('原始信号');grid on;

hold off

%互相关函数

X1=fft(x1,2*N-1);

X2=fft(x2,2*N-1);

Sxy=X1.*conj(X2);

%Cxy=fftshift(ifft(Sxy));

Cxy=fftshift(ifft(Sxy./abs(Sxy)));

subplot(212);

t1=(-N+1:N-1)/Fs;

plot(t1,Cxy,'b');

title('Rx1x2');xlabel('t/s');ylabel('Rx1x2(t)');grid on [max,location]=max(Cxy);

%d=location-N/2-1

d=location-N

Delay=d/Fs %求得时间延迟

运行程序得到的结果是：

d =

1

Delay =

0.0020

我们可以看见结果是d=1,delay=0.0020，而实例中给出的时延为d/fs=0.016，这并不表示PHAT-GCC算法是错误的，只是因为，我们在信号中加入了均值为0，方差为1的高斯白噪音，所以才会导致了误差的存在。

三、ROTH-GCC模拟

clear;

N=1024;%信号长度

fs=500;%采样频率

n=0:N-1;

t=n/fs;%时间序列

a1=5;%信号幅度

a2=5;%信号幅度

d=2;%延迟点数

x1=a1*sin(2*pi*10*n/fs);

x2=a2*sin(2*pi*10*(n+d)/fs);

%x2=awgn(x1./4,-3); %噪声强度大于信号

%x2=x2 .* hamming(N);

x1=x1+randn(size(x1)); %加入噪声

x2=x2+randn(size(x2));

S1=fft(x1,2*N-1);

S2=fft(x2,2*N-1);

S12 = S1.* conj(S2);

S11 = S1.* conj(S1);

R1 =real(fftshift(ifft(S12./abs(S11))));

ts=(-N+1:N-1)/fs;

plot(ts,R1);

xlabel('时间/s');ylabel('R1(t)');

title('互相关函数');

[max,location]=max(R1);

%d=location-N/2-1

d=location-N

Delay=d/fs

运行程序的结果为：

d =

4

Delay =

0.0080

四、SCOT-GCC模拟

clear;

N=1024;%信号长度

fs=1000;%采样频率

n=0:N-1;

t=n/fs;%时间序列

ts = 1/fs * (-N + (1 : 2*N - 1)); %互相关时间序列

a1=5;%信号幅度

a2=5;%信号幅度

d=26;%延迟点数

x1=a1*sin(2*pi*10*t)+1.9*sin(2*pi*18*t)+2.8*sin(2*pi*55*t);

x2=a2*sin(2*pi*10*(n+d)/fs)+1.9*sin(2*pi*18*(n+d)/fs)+2.8*sin(2*pi*55 *(n+d)/fs);

%x2=awgn(x1./4,-3); %噪声强度大于信号

%x2=x2 .* hamming(N);

x=awgn(x1,20); %加入噪声

y=awgn(x2,0.001);

S1=fft(x,2*N-1);

S2=fft(y,2*N-1);

X = S1.* conj(S2);

X11 = S1.* conj(S1);

X22 = S2.* conj(S2);

Y=sqrt(X11.*X22);

R1 =real(fftshift(ifft(X./Y)));

plot(ts,R1);

xlabel('时间/s');ylabel('R1(t)');

title('ifft计算结果')

[max,location]=max(R1);

%d=location-N/2-1

d=location-N

Delay=d/fs

运行程序的结果是：

d =

8

Delay =

0.0080

五、相同信噪比不同算法的比较

clear all; clc; close all;

N=1024; %长度

Fs=500; %采样频率

n=0:N-1;

t=n/Fs; %时间序列

a1=30; %信号幅度

a2=30;

d=9; %延迟点数

x1=a1*cos(2*pi*10*n/Fs); %信号1 x1=awgn(x1,20); %加噪声

%x1=x1.*hamming(max(size(x1)))';%加窗x2=a2*cos(2*pi*10*(n+d)/Fs); %信号2 x2=awgn(x2,20);

%x2=x2.*hamming(max(size(x2)))';%加窗subplot(511);

plot(t,x1,'r');

axis([-0.2 2 -40 40]);

hold on;

plot(t,x2,':');

axis([-0.2 2 -40 40]);

legend('x1信号', 'x2信号');

xlabel('时间/s');ylabel('x1(t) x2(t)');

title('原始信号');grid on;

%互相关函数

tic

X1=fft(x1,2*N-1);

X2=fft(x2,2*N-1);

Sxy=X1.*conj(X2);

%Cxy=fftshift(ifft(Sxy));

%GCC

Cxy=fftshift(ifft(Sxy));

subplot(512);

t1=(-N+1:N-1)/Fs;

plot(t1,Cxy,'b');

title('GCC');xlabel('t/s');ylabel('Cxy');grid on;

[max1,location1]=max(Cxy);

%d=location-N/2-1

d1=location1-N

Delay1=d1/Fs %求得时间延迟

toc

%phat-gcc

tic

X1=fft(x1,2*N-1);

X2=fft(x2,2*N-1);

Sxy=X1.*conj(X2);

Pxy=fftshift(ifft(Sxy./abs(Sxy)));

subplot(513);

t1=(-N+1:N-1)/Fs;

plot(t1,Pxy,'b');

title('phat-gcc');xlabel('t/s');ylabel('Pxy');grid on;

[max2,location2]=max(Pxy);

%d=location-N/2-1

d2=location2-N

Delay2=d2/Fs %求得时间延迟

toc

%rhat-gcc

tic

X1=fft(x1,2*N-1);

X2=fft(x2,2*N-1);

Sxy=X1.*conj(X2);

S11 = X1.* conj(X1);

Rxy=fftshift(ifft(Sxy./abs(S11)));

subplot(514);

t1=(-N+1:N-1)/Fs;

plot(t1,Rxy,'b');

title('phat-gcc');xlabel('t/s');ylabel('Rxy');grid on;

[max3,location3]=max(Rxy);

%d=location-N/2-1

d3=location3-N

Delay3=d3/Fs %求得时间延迟

toc

%scot-gcc

tic

X1=fft(x1,2*N-1);

X2=fft(x2,2*N-1);

Sxy=X1.*conj(X2);

S11 = X1.* conj(X1);

S22 = X2.* conj(X2);

Y=sqrt(S11.*S22);

SCxy=fftshift(ifft(Sxy./Y));

subplot(515);

t1=(-N+1:N-1)/Fs;

plot(t1,SCxy,'b');

title('scot-gcc');xlabel('t/s');ylabel('SCxy');grid on;

[max4,location4]=max(SCxy);

%d=location-N/2-1

d4=location4-N

Delay4=d4/Fs %求得时间延迟

toc

SNR=0时

●SNR=10时：

●SNR=20时

SNR=50时

分析：从运行结果上来看，在时间上，基本互相关、PHAT加权、ROTH加权和SCOT 加权四种算法的运行时间基本相同；但是从峰度的锐化来说，这四种方式的时延

估计的准确性随着信噪比的降低而恶化，互相关函数峰值的尖锐程度随信噪比的降低而降低。对于SCOT加权来说，随着信噪比的降低，性能急剧下降。基本互相关函数和RHOT加权虽然有一定的抗噪能力，但随着信噪比的降低，其波动程度明显加强，特别是对外围的噪声、反射和有限观测数据很敏感，会造成峰值不明显；对于PHAT加权，在较高的信噪比的时候，表现出了波动小、峰值尖锐的特性，在降低信噪比时，也表现出了较强的抗干扰性。

总结：在这些互相关函数的算法中，PHAT加权有比较好的性质。

自相关函数与互相关函数 不错的材料

2.4.3 相关函数 １．自相关函数 自相关函数是信号在时域中特性的平均度量，它用来描述信号在一个时刻的取值与另一时刻取值的依赖关系，其定义式为 （2.4.6） 对于周期信号，积分平均时间T为信号周期。对于有限时间内的信号，例如单个脉冲，当T趋于无穷大时，该平均值将趋于零，这时自相关函数可用下式计算 （2.4.7） 自相关函数就是信号x(t)和它的时移信号x(t+τ)乘积的平均值，它是时移变量τ的函数。 例如信号的自相关函数为 若信号是由两个频率与初相角不同的频率分量组成，即 ，则

对于正弦信号，由于，其自相关函数仍为 由此可见，正弦（余弦）信号的自相关函数同样是一个余弦函数。它保留了原信号的频率成分，其频率不变，幅值等于原幅值平方的一半，即等于该频率分量的平均功率，但丢失了相角的信息。 自相关函数具有如下主要性质： （1）自相关函数为偶函数，，其图形对称于纵轴。因此，不论时移方向是导前还是滞后（τ为正或负），函数值不变。 （2）当τ＝0时，自相关函数具有最大值，且等于信号的均方值，即 （2.4.8）（3）周期信号的自相关函数仍为同频率的周期信号。 （4）若随机信号不含周期成分，当τ趋于无穷大时，趋于信号平均值的平方，即 （2.4.9） 实际工程应用中，常采用自相关系数来度量其不同时刻信号值之间的相关程

度，定义式为 （2.4.10） 当τ＝0时，＝1，说明相关程度最大；当τ＝∞时，，说明信号x(t)与 x(t+τ)之间彼此无关。由于，所以。值的大小表示信号相关性的强弱。 自相关函数的性质可用图2.4.3表示。 图2.4.3 自相关函数的性质 常见四种典型信号的自相关函数如图2.4.4所示，自相关函数的典型应用包括：（1）检测信号回声（反射）。若在宽带信号中存在着带时间延迟的回声，那么该信号的自相关函数将在处也达到峰值（另一峰值在处），这样可根据确定反射体的位置，同时自相关系数在处的值将给出反射信号相对强度的度量。 时间历程自相关函数图形

现代测试技术习题解答--第二章--信号的描述与分析---副本

第二章 信号的描述与分析 补充题2-1-1 求正弦信号0()sin()x t x ωt φ=+的均值x μ、均方值2 x ψ和概率密度函数 p (x )。 解答： (1)0 00 11lim ()d sin()d 0T T x T μx t t x ωt φt T T →∞== +=? ? ，式中02π T ω = —正弦信号周期 (2) 2 222 2 2 0000 1 1 1cos 2() lim ()d sin ()d d 22 T T T x T x x ωt φψx t t x ωt φt t T T T →∞-+== += = ? ? ? (3)在一个周期内 012ΔΔ2Δx T t t t =+= 000 2Δ[()Δ]lim x x T T T t P x x t x x T T T →∞<≤+=== Δ0Δ000 [()Δ]2Δ2d ()lim lim ΔΔd x x P x x t x x t t p x x T x T x →→<≤+==== 正弦信号 x

2-8 求余弦信号0()sin x t x ωt 的绝对均值x μ和均方根值rms x 。 2-1 求图示2.36所示锯齿波信号的傅里叶级数展开。

2-4周期性三角波信号如图2.37所示，求信号的直流分量、基波有效值、信号有效值及信号的平均功率。

2-1 求图示2.36所示锯齿波信号的傅里叶级数展开。 补充题2-1-2 求周期方波（见图1-4）的傅里叶级数（复指数函数形式），划出|c n|–ω和φn–ω

图，并与表1-1对比。 解答：在一个周期的表达式为 00 (0)2 () (0) 2 T A t x t T A t ? --≤

三角函数正余弦函数的图像及性质复习汇总

一、正弦函数和余弦函数的图象： 正弦函数sin y x =和余弦函数cos y x =图象的作图方法：五点法：先取横坐标分别为0，3,,,222ππ ππ 的五点，再用光滑的曲线把这五点连接起来，就得到正弦曲线和余弦曲线在一个周期内的图象。 二、正弦函数sin ()y x x R =∈、余弦函数cos ()y x x R =∈的性质： （1）定义域：都是R 。 （2）值域： 1、都是[]1,1-， 2、sin y x =，当()22 x k k Z π π=+ ∈时，y 取最大值1；当()322 x k k Z π π=+ ∈时，y 取最小值－1； 3、cos y x =，当()2x k k Z π=∈时，y 取最大值1，当()2x k k Z ππ=+∈时，y 取最小值－1。 例：（1）若函数sin(3)6 y a b x π=-+的最大值为23，最小值为21 -，则=a __，=b ＿

（答：,12 a b ==或1b =-）； ⑵ 函数y=-2sinx+10取最小值时，自变量x 的集合是_________________________。 （3）周期性： ①sin y x =、cos y x =的最小正周期都是2π； ②()sin()f x A x ω?=+和()cos()f x A x ω?=+的最小正周期都是2|| T πω=。 例：(1)若3 sin )(x x f π=，则(1)(2)(3)(2003)f f f f ++++＝___（答：0） ； ⑵．下列函数中，最小正周期为π的是（ ） A.cos 4y x = B.sin 2y x = C.sin 2x y = D.cos 4x y = （4）奇偶性与对称性： 1、正弦函数sin ()y x x R =∈是奇函数，对称中心是()(),0k k Z π∈，对称轴是直线()2 x k k Z π π=+ ∈； 2、余弦函数cos ()y x x R =∈是偶函数，对称中心是(),02k k Z ππ? ?+∈ ???，对称轴是直线()x k k Z π=∈ （正(余)弦型函数的对称轴为过最高点或最低点且垂直于x 轴的直线，对称中心为图象与x 轴的交点）。 例：（1）函数522y sin x π?? =- ??? 的奇偶性是______（答：偶函数）； （2）已知函数31f (x )ax b sin x (a,b =++为常数），且57f ()=，则5f ()-=______（答：－5）； （5）单调性： ()sin 2,222y x k k k Z ππππ??=-+∈????在上单调递增，在()32,222k k k Z ππππ? ?++∈????单调递减； cos y x =在[]()2,2k k k Z πππ+∈上单调递减，在[]()2,22k k k Z ππππ++∈上单调递增。特别提醒，别忘了k Z ∈！ ⑴函数y=sin2x 的单调减区间是（ ）

正弦函数余弦函数的性质

正弦函数余弦函数的性质 教学目标 1．掌握y＝sin x(x∈R)，y＝cos x(x∈R)的周期性、奇偶性、单调性和最值．(重点) 2．会用正弦函数、余弦函数的性质解决一些简单的三角函数问题．(难点) 3．了解周期函数、周期、最小正周期的含义．(易混点) [基础·初探] 教材整理1函数的周期性 阅读教材P34～P35“例2”以上部分，完成下列问题． 1．函数的周期性 (1)对于函数f(x)，如果存在一个非零常数T，使得当x取定义域内的每一个值时，都有f(x＋T)＝f(x)，那么函数f(x)就叫做周期函数，非零常数T叫做这个函数的周期． (2)如果在周期函数f(x)的所有周期中存在一个最小的正数，那么这个最小正数就叫做f(x)的最小正周期． 2．两种特殊的周期函数 (1)正弦函数是周期函数，2kπ(k∈Z且k≠0)都是它的周期，最小正周期是2π． (2)余弦函数是周期函数，2kπ(k∈Z且k≠0)都是它的周期，最小正周期是2π． 函数y＝2cos x＋5的最小正周期是________．

解：函数y ＝2cos x ＋5的最小正周期为T ＝2π. 【答案】 2π 教材整理2 正、余弦函数的奇偶性 阅读教材P 37“思考”以下至P 37第14行以上内容，完成下列问题． 1．对于y ＝sin x ，x ∈R 恒有sin(－x )＝－sin x ，所以正弦函数y ＝sin x 是奇函数，正弦曲线关于原点对称． 2．对于y ＝cos x ，x ∈R 恒有cos(－x )＝cos x ，所以余弦函数y ＝cos x 是偶函数，余弦曲线关于y 轴对称． 判断函数f (x )＝sin ? ?? ?? 2x ＋ 3π2的奇偶性． 解：因为f (x )＝sin ? ???? 2x ＋3π2＝－cos 2x . 且f (－x )＝－cos(－2x )＝－cos 2x ＝f (x )，所以f (x )为偶函数． 教材整理3 正、余弦函数的图象和性质 阅读教材P 37～P 38“例3”以上内容，完成下列问题．

自相关函数和互相关函数的利用MATLAB计算和作图

互相关函数，自相关函数计算和作图 1.自相关和互相关的概念。 ●互相关函数是描述随机信号x(t),y(t)在任意两个不同时刻t1，t2间的相关程度。 ●自相关函数是描述随机信号x(t)在任意两个不同时刻t1，t2间的相关程度。 互相关函数是在频域内两个信号是否相关的一个判断指标，把两测点之间信号的互谱与各自的自谱联系了起来。它能用来确定输出信号有多大程度来自输入信号，对修正测量中接入噪声源而产生的误差非常有效。 -----------------------------------------------------------------------------------事实上，在图象处理中，自相关和互相关函数的定义如下：设原函数是f(t)，则自相关函数定义为R(u)=f(t)*f(-t)，其中*表示卷积；设两个函数分别是f(t)和g(t)，则互相关函数定义为R(u)=f(t)*g(-t)，它反映的是两个函数在不同的相对位置上互相匹配的程度。 2.利用matlab中实现这两个相关并用图像显示： 自相关函数： dt=.1; t=[0:dt:100];x=cos(t); [a,b]=xcorr(x,'unbiased'); plot(b*dt,a)

互相关函数：把[a,b]=xcorr(x,'unbiased');改为[a,b]=xcorr(x,y,'unbiased');便可。 3.实现过程： 在Matalb中，求解xcorr的过程事实上是利用Fourier变换中的卷积定理进行的，即 R(u)=ifft(fft(f)×fft(g))，其中×表示乘法，注：此公式仅表示形式计算，并非实际计算所用的公式。当然也可以直接采用卷积进行计算，但是结果会与xcorr的不同。事实上，两者既然有定理保证，那么结果一定是相同的，只是没有用对公式而已。下面是检验两者结果相同的代码： dt=.1; t=[0:dt:100]; x=3*sin(t); y=cos(3*t); subplot(3,1,1); plot(t,x); subplot(3,1,2); plot(t,y); [a,b]=xcorr(x,y); subplot(3,1,3); plot(b*dt,a); yy=cos(3*fliplr(t));%or use:yy=fliplr(y); z=conv(x,yy); pause; subplot(3,1,3); plot(b*dt,z,'r'); 即在xcorr中不使用scaling。

Matlab自相关函数和互相关函数的计算和作图

自相关函数(Autocorrelation function，缩写ACF)是信号处理、时间序列分析中常用的数学工具，反映了同一序列在不同时刻的取值之间的相关程度。 自相关函数在不同的领域，定义不完全等效。在某些领域，自相关函数等同于自协方差(autocovariance)。 信号处理 在信息分析中，通常将自相关函数称之为自协方差方程。用来描述信息在不同时间τ的，信息函数值的相关性。 ，其中“*”是卷积算符，为取共轭 自相关函数的性质 以下以一维自相关函数为例说明其性质，多维的情况可方便地从一维情况推广得到。 ?对称性：从定义显然可以看出R(i) = R(?i)。连续型自相关函数为偶函数当f为实函数时，有： 当f是复函数时，该自相关函数是厄米函数，满足： 其中星号表示共轭。 ?连续型实自相关函数的峰值在原点取得，即对于任何延时τ，均有 。该结论可直接有柯西-施瓦茨不等式得到。离散型自相关函数亦有此结论。 ?周期函数的自相关函数是具有与原函数相同周期的函数。 ?两个相互无关的函数（即对于所有τ，两函数的互相关均为0）之和的自相关函数等于各自自相关函数之和。 ?由于自相关函数是一种特殊的互相关函数，所以它具有后者的所有性质。

?连续时间白噪声信号的自相关函数是一个δ函数，在除τ = 0 之外的所有点均为0。 ?维纳-辛钦定理（Wiener–Khinchin theorem）表明，自相关函数和功率谱密度函数是一对傅里叶变换对： ?实值、对称的自相关函数具有实对称的变换函数，因此此时维纳-辛钦定理中的复指数项可以写成如下的余弦形式： 白噪声的自相关函数为δ函数： 自相关函数和偏相关函数的问题 在时间序列分析的研究中，首先是判别时间序列的稳定性，如果时间序列是平稳的就可以计算这些数据的自相关函数和偏相关函数。 如果自相关函数是拖尾的，偏相关函数是截尾的，那麽数据符合AR（P）模型。 如果自相关函数是截尾的，偏相关函数是拖尾的，那麽数据复合MA( Q )模型 如果自相关函数和偏相关函数都是拖尾的，那麽数据复合ARMA( P,Q )模型。 自相关函数和互相关函数的matlab计算和作图 1. 首先说说自相关和互相关的概念。 这个是信号分析里的概念，他们分别表示的是两个时间序列之间和同一个时间序列在任意两个不同时刻的取值之间的相关程度，即互相关函数是描述随机信号x(t),y(t)在任意两个不同时刻t1，t2的取值之间的相关程度，自相关函数是描述随机信号x(t)在任意两个不同时刻t1，t2的取值之间的相关程度。互相关函数给出了在频域内两个信号是否相关的一个判断指标，把两测点之间信号的互谱与

正余弦函数的图像与性质(周期性)

第一课时 题目：正弦函数、余弦函数的图象 授课时间：3月25日，星期一 课型：新授课 教学目标： 理解借助单位圆中的三角函数线（正弦线）画出y sin x =的图象，进而画出 y cos x =的图象；会用“五点法”画y sin x =和y cos x =在一个周期内的简图。 教学重点和难点： 重点：利用三角函数线画正弦函数[]x 0,2 蝡的图象，用“五点法”画y sin x =和 y cos x =在一个周期内的简图。 难点：正弦函数与余弦函数图象间的关系、图象变换。 学情分析： 学生在之前已经学了一次函数、二次函数、指数函数、对数函数和幂函数，已掌握了一些基础函数的图像和性质，并了解一些函数图像的画法。而且刚分班学生的学习动力很足，但学生分析、理解能力较差，对具体形象的事物比较感兴趣，但对学习抽象理论知识存在畏难情绪，缺乏学习主动性，因此在教学中要注意引导学生积极思考和多动手画图练习。 教学方法： 通过多媒体展示正弦函数的形成，是学生更直观形象的了解正弦函数的形成，加深印象增加兴趣。并配合适当讲授法。在五点法画图中要学生动手实践，加深印象和理解。 教具、学具的准备：多媒体、直尺、圆规 教学过程： （一）知识链接 1、正弦线的概念 2、诱导公式（六） （二）情景设置 在初中和必修一的函数学习中，我们知道函数的图像为我们解决相关的函数问题提供了重要的方法和工具，那么三角函数的图像是怎样的呢？ 这节课让我们来共同探讨正、余弦函数的图像问题。 【设计意图】从原有知识出发，类比联想，引入问题情景，学生主动参与，积极思考 （三）课题导入 提问1、如何作正弦函数的图象？ ①列表描点法： 步骤：列表、描点、连线 大家试着画出正弦函数sin y x =[]0,2x π∈的图像

自相关和互相关

1. 首先说说自相关和互相关的概念。 这个是信号分析里的概念，他们分别表示的是两个时间序列之间和同一个时间序列在任意两个不同时刻的取值之间的相关程度，即互相关函数是描述随机信号x(t),y(t)在任意两个不同时刻t1，t2的取值之间的相关程度，自相关函数是描述随机信号x(t)在任意两个不同时刻t1，t2的取值之间的相关程度。 自相关函数是描述随机信号X(t)在任意两个不同时刻t1，t2的取值之间的相关程度；互相关函数给出了在频域内两个信号是否相关的一个 判断指标，把两测点之间信号的互谱与各自的自谱联系了起来。它能用来确定输出信号有多大程度来自输入信号，对修正测量中接入噪声源而产生的误差非常有效. 事实上，在图象处理中，自相关和互相关函数的定义如下：设原函数是f(t)，则自相关函数定义为R(u)=f(t)*f(-t)，其中*表示卷积；设两个函数分别是f(t)和g(t)，则互相关函数定义为R(u)=f(t)*g(-t)，它反映的是两个函数在不同的相对位置上互相匹配的程度。 那么，如何在matlab中实现这两个相关并用图像显示出来呢？ dt=.1; t=[0:dt:100]; x=cos(t); [a,b]=xcorr(x,'unbiased'); plot(b*dt,a) 上面代码是求自相关函数并作图，对于互相关函数，稍微修改一下就可以了，即把[a,b]=xcorr(x,'unbiased');改为[a,b]=xcorr(x,y,'unbiased');便可。 2. 实现过程： 在Matalb中，求解xcorr的过程事实上是利用Fourier变换中的卷积定理进行的，即R(u)=ifft(fft(f)×fft(g))，其中×表示乘法，注：此公式仅表示形式计算，并非实际计算所用的公式。当然也可以直接采用卷积进行计算，但是结果会与xcorr的不同。事实上，两者既然有定理保证，那么结果一定是相同的，只是没有用对公式而已。下面是检验两者结果相同的代码： dt=.1; t=[0:dt:100]; x=3*sin(t); y=cos(3*t); subplot(3,1,1); plot(t,x); subplot(3,1,2); plot(t,y); [a,b]=xcorr(x,y); subplot(3,1,3); plot(b*dt,a); yy=cos(3*fliplr(t)); % or use: yy=fliplr(y); z=conv(x,yy); pause;

(完整版)相关函数及其应用

第一专题: 1、相关函数的计算方法（方法的选取及选取的原因） 2、相关函数的性质和应用（选一个应用讲解并仿真） 相关函数的计算方法 利用计算机计算自相关估值有两种方法。一种是直接方法，先计算出随机信号和它的滞后序列的乘积，再取其平均值即得相关函数的估计值。另一种是间接方法，先用快速变换算法计算随机序列的功率谱密度，再作反变换计算出相关函数。 1、直接计算 （1）公式计算 对于时域信号，可以直接按照下面的公式来计算其相关函数，两个能量信号 (t)s 1和(t)2s 互相关函数的定义为 ?+∞ ∞ +=-2112x )dt (t (t)s s (x )R 功率信号(t)s 1和(t)2s 的互相关函数定义为 ?+∞→+=2 /2 /-2112x)dt (t (t)s s 1lim (x)T T T T R （2）自相关函数的估计 在计算机处理数字信号的过程中，一般是对自相关函数进行估计来计算。 假定X[k]是宽平稳各态遍历信号，x[k]是其中的一个样本，其自相关可由单一样本x[k]的时间平均来实现，即 ∑==∞→++=N N N R k -k N x n]x [k]x [k 121lim [n] 由于在实际中仅能得到随即信号的一次样本序列x[0]，x[1]，……，x[N-1]，用[k]x N 来表示，因此只能得到自相关函数的估计，即 ∑-=+= 1 k N N n] [k [k]x x 1(n)N x N r

上式中，对每一固定延迟n ，可利用的数据只有N-n 个，所以自相关函数的估计可以表示成 ∑-=+= 1-n 0 k N N ] n [k [k]x x 1 (n)N x N r 2、间接算法 间接方法是利用自相关函数与其功率谱密度互为一对傅里叶变换的关系来计算的。在数字信号处理中，利用快速傅里叶变换的方法计算出功率谱密度函数的估值，然后再计算它的傅里叶反变换，即得自相关函数估值。由于采用了快速傅里叶变换算法，计算速度较快。如当N =2P 时，间接算法所需要的运算量约为8NP 次实数乘加运算。因此,两种方法的速度比是 速度比= 8p m p 8m =N N 如P ＝13，m ＝0.1N ＝819，则比值约为8，即间接算法比直接算法约快8倍。 对于能量信号，计算R(x)可用以下公式： ? +∞ ∞ =-fx j22 df e )f ((x )πS R 对于功率信号计算R(x)可用以下公式： ? ∑∞+∞ ∞ ∞ =-fx j20-2 df )e nf -(f δ(f) (x )πC R 相关函数的性质及应用 1、自相关函数的性质及其应用 自相关函数具有如下性质： （1） R(x)为实函数； （2） R(x)为偶函数，即R(x)=R(-x)； （3） R(0)等于信号的均方值； （4） 对于各态历经性的随机信号s(t)有R(x)在R(0)处取得最大值； （5） 当随机信号s(t)的均值为u 时，有2x u (x)lim =∞ →R ，当s(t)为确定性信号时， 当x →∞时，自相关函数值不为均值的平方；

三角函数正余弦函数的图像及性质复习汇总

课题三角函数的图像及性质 1.借助单位圆中的三角函数线推导出诱导公式( π2/±α , π的±正α弦、余弦、正切) 教学目标 2.利用单位圆中的三角函数线作出y sin x,x R的图象，明确图象的形状； 3.根据关系cosx sin(x ) ，作出y cosx,x R的图象； 2 4.用“五点法”作出正弦函数、余弦函数的简图，并利用图象解决一些有关问题； 重点、难点 1、正确地用三角函数线表示任意角的三角函数值 2、作余弦函数的图象。 教学内容 、正弦函数和余弦函数的图象： -1 正弦函数y sin x 和余弦函数y cos x图象的作图方法：五点法：先取横坐标分别为0，, ,3 ,2 22 的五点，再用光滑的曲线把这五点连接起来，就得到正弦曲线和余弦曲线在一个周期内的图象。 二、正弦函数y sin x(x R) 、余弦函数y cosx(x R) 的性质： ( 1)定义域：都是R。 (2)值域： 1、都是1,1 ， 2、y sinx ，当x 2k k 2 3、y cosx ，当x 2k k Z 例： ( 1)若函数y a bsin(3 x Z 时，y 取最大值1 ；当x 时，y 取最大值1，当x 2k ) 的最大值为3，最小值为 62 3 2k 3 k Z 时，y 取最小值－1； 2 k Z 时，y 取最小值－ 1 。 1，则 a __， b ＿ 2 3 y -2 1 y=cosx -3 -5 -32 -4 -7 -2 -3 22

1 答： a 1 2,b 1或b 1)； ⑵ 函数 y=-2sinx+10 取最小值时，自变量 x 的集合是 3）周期性 ： （正（余）弦型函数的对称轴为过最高点或最低点且垂直于 x 轴的直线，对称中心为图象与 x 轴的交 点）。 5）单调性 ： 别忘了 k Z ！ ⑴函数 y=sin2x 的单调减区间是（ ① y sin x 、 y cos x 的最小正周期都是 2 ； ② f ( x) A sin( x )和 f (x) Acos( 2 x ） 的最小正周期都是 T 2 sin 3x ，则 f （1） f （2） ⑵．下列函数中，最小正周期为 例： (1)若 f (x) f (3) L 的是（ A. y cos 4x B. y sin 2x C.y f (2003) ＝ 答： 0）； x sin 2 D.y x cos 4 （ 4）奇偶性与对称性 ： 1、正弦函数 y sin x （ x R ） 是奇函 数， 对称中心是 k ,0 k Z ，对称轴是直线 x k k Z ； 2 2、余弦函数 y cosx （x R ） 是偶函数， 对称中心是 k 2 ,0 k Z ，对称轴是直线 x k k Z 5 例：（1） 函数 y sin 5 2 2x 的奇偶性是 答：偶函数）； 2）已知函数 f （ x ） a x bsin 3 x 1( a,b 为常数)， 且 f (5 ) 7， 则 f ( 5) 答：－ 5）； y sin x 在 2k , 2k 2 k Z 上单调递增，在 2k , 2k 2 3 k Z 单调递减； 2 y cosx 在 2k ,2 k Z 上单调递减，在 2k ,2k k Z 上单调递增。 特别提醒 ，

自相关与互相关函数

相关函数 １．自相关函数 自相关函数是信号在时域中特性的平均度量，它用来描述信号在一个时刻的取值与 另一时刻取值的依赖关系，其定义式为 （2.4.6） 对于周期信号，积分平均时间T为信号周期。对于有限时间的信号，例如单个脉 冲，当T趋于无穷大时，该平均值将趋于零，这时自相关函数可用下式计算 （2.4.7） 自相关函数就是信号x(t)和它的时移信号x(t+τ)乘积的平均值，它是时移变量τ的函数。 例如信号的自相关函数为 若信号是由两个频率与初相角不同的频率分量组成，即 ，则

对于正弦信号，由于，其自相关函数仍为 由此可见，正弦（余弦）信号的自相关函数同样是一个余弦函数。它保留了原信号的频率成分，其频率不变，幅值等于原幅值平方的一半，即等于该频率分量的平均功率 ，但丢失了相角的信息。 自相关函数具有如下主要性质： （1）自相关函数为偶函数，，其图形对称于纵轴。因此，不论时移方向是导前还是滞后（τ为正或负），函数值不变。 （2）当τ＝0时，自相关函数具有最大值，且等于信号的均方值，即 （2.4.8）（3）周期信号的自相关函数仍为同频率的周期信号。 （4）若随机信号不含周期成分，当τ趋于无穷大时，趋于信号平均值的平方，即 （2.4.9）实际工程应用中，常采用自相关系数来度量其不同时刻信号值之间的相关程度，定义式为 （2.4.10）

当τ＝0时，＝1，说明相关程度最大；当τ＝∞时，，说明信号x(t)与x(t+τ)之间彼此无关。由于，所以。值的大小表示信号相关性的强弱。 自相关函数的性质可用图2.4.3表示。 图2.4.3 自相关函数的性质 常见四种典型信号的自相关函数如图2.4.4所示，自相关函数的典型应用包括： （1）检测信号回声（反射）。若在宽带信号中存在着带时间延迟的回声，那么该 信号的自相关函数将在处也达到峰值（另一峰值在处），这样可根据确定 反射体的位置，同时自相关系数在处的值将给出反射信号相对强度的度量。 时间历程自相关函数图形 正 弦 波

正、余弦函数的图象和性质

xx －xx 学年度下学期 高中学生学科素质训练 高一数学同步测试（6）—正、余弦函数的图象和性质 一、选择题（每小题5分，共60分，请将正确答案填在题后的括号内） 1．函数)4 sin(π +=x y 在闭区间（ ）上为增函数. （ ） A ．]4 ,43[ππ- B ．]0,[π- C ．]4 3 ,4[ππ- D ．]2 ,2[π π- 2．函数)4 2sin(log 2 1π + =x y 的单调减区间为 （ ） A ．)(],4(Z k k k ∈- ππ π B ．)(]8,8(Z k k k ∈+- π πππ C ．)(] 8 ,83(Z k k k ∈+-π πππ D ．)(]8 3 ,8(Z k k k ∈++ππππ 3．设a 为常数，且π20,1≤≤>x a ，则函数1sin 2cos )(2 -+=x a x x f 的最大值为 （ ） A ．12+a B ．12-a C ．12--a D ．2 a 4．函数)2 5 2sin(π+=x y 的图象的一条对称轴方程是 （ ） A ．2 π - =x B ．4 π - =x C ．8π=x D ．π4 5=x 5．方程x x lg sin =的实根有 （ ） A ．1个 B ．2个 C ．3个 D ．无数个 6．下列函数中，以π为周期的偶函数是 （ ） A ．|sin |x y = B ．||sin x y = C ．)32sin(π + =x y D ．)2 sin(π +=x y 7．已知)20(cos π≤≤=x x y 的图象和直线y=1围成一个封闭的平面图形，该图形的面积 是 （ ） A ．4π B ．2π C ．8 D ．4 8．下列四个函数中为周期函数的是 （ ）

自相关函数

自相关函数在不同的领域，定义不完全等效。在某些领域，自相关函数等 同于自协方差(autocovariance)。 统计学 R(k) = \frac{E[(X_i - \mu)(X_{i+k} - \mu)]}{\sigma^2} 信号处理 R_f(\tau) = f(\tau) * f^*(-\tau)= \int_{-\infty}^{\infty} f(t+\tau)f^*(t)\, dt = \int_{-\infty}^{\infty} f(t)f^*(t-\tau)\, dt，其中“*”是卷积算符，(\cdot)^*为取共轭。 同一时间函数在瞬时t和t+a的两个值相乘积的平均值作为延迟时间t 的函数，它是信号与延迟后信号之间相似性的度量。延迟时间为零时，则 成为信号的均方值，此时它的值最大。 编辑本段 自相关函数的性质 以下以一维自相关函数为例说明其性质，多维的情况可方便地从一维 情况推广得到。 对称性：从定义显然可以看出R(i) = R(?i)。连续型自相关函数为偶 函数 当f为实函数时，有： R_f(-\tau) = R_f(\tau)\, 当f是复函数时，该自相关函数是厄米函数，满足： R_f(-\tau) = R_f^*(\tau)\, 其中星号表示共轭。 连续型实自相关函数的峰值在原点取得，即对于任何延时τ，均有 |R_f(\tau)| \leq R_f(0)。该结论可直接有柯西-施瓦兹不等式得到。离 散型自相关函数亦有此结论。 周期函数的自相关函数是具有与原函数相同周期的函数。 两个相互无关的函数（即对于所有τ，两函数的互相关均为0）之和 的自相关函数等于各自自相关函数之和。 由于自相关函数是一种特殊的互相关函数，所以它具有后者的所有性质。 连续时间白噪声信号的自相关函数是一个δ函数，在除τ = 0 之外 的所有点均为0。 维纳-辛钦定理（Wiener–Khinchin theorem）表明，自相关函数和功 率谱密度函数是一对傅里叶变换对： R(\tau) = \int_{-\infty}^\infty S(f) e^{j 2 \pi f \tau} \, df

自相关函数和互相关函数计算和作图的整理之欧阳家百创编

自相关函数和互相关函数计算和作图的整理 欧阳家百（2021.03.07） 1. 首先说说自相关和互相关的概念。 --[转版友gghhjj]------------------------------------------------------------------------------------- 这个是信号分析里的概念，他们分别表示的是两个时间序列之间和同一个时间序列在任意两个不同时刻的取值之间的相关程度，即互相关函数是描述随机信号 x(t),y(t)在任意两个不同时刻t1，t2的取值之间的相关程度，自相关函数是描述随机信号x(t)在任意两个不同时刻t1，t2的取值之间的相关程度。 ---------------------------------------------------------------------------------------------------------------------------------------------- --[转版友hustyoung]----------------------------------------------------------------------------------- 自相关函数是描述随机信号X(t)在任意两个不同时刻t1，t2的取值之间的相关程度；互相关函数给出了在频域内两个信号是否相关的一个判断指标，把两测点之间信号的互谱与各自的自谱联系了起来。它能用来确定输出信号有多大程度来自输入信号，对修正测量中接入噪声源而产生的误差非常有效。 ---------------------------------------------------------------------------------------------------------------------------------------------- 事实上，在图象处理中，自相关和互相关函数的定义如下：设原函数是f(t)，则自相关函数定义为R(u)=f(t)*f(-t)，其中*表示卷积；设两个函数分别是f(t)和g(t)，则互相关函数定义为R(u)=f(t)*g(-t)，它反映的是两个函数在不同的相对位置上互相匹配的程度。 那么，如何在matlab中实现这两个相关并用图像显示出来呢？这个问题happy教授给出了完整答案： -----------[转happy教授]--------------------- dt=.1; t=[0:dt:100]; x=cos(t); [a,b]=xcorr(x,'unbiased'); plot(b*dt,a) ----------------------------------------------------- 上面代码是求自相关函数并作图，对于互相关函数，稍微修改一下就可以了，即把[a,b]=xcorr(x,'unbiased');改为[a,b]=xcorr(x,y,'unbiased');便可。 2. 实现过程： 在Matalb中，求解xcorr的过程事实上是利用Fourier变换中的卷积定理进行的，即R(u)=ifft(fft(f)×fft(g))，其中 ×表示乘法，注：此公式仅表示形式计算，并非实际计算所用的公式。当然也可以直接采用卷积进行计算，但是结果会与xcorr的不同。事实上，两者既然有定理保证，那么结果一定是相同的，只是没有用对公式而已。下面是检验两者结果相同的代码： dt=.1; t=[0:dt:100]; x=3*sin(t); y=cos(3*t); subplot(3,1,1); plot(t,x); subplot(3,1,2); plot(t,y); [a,b]=xcorr(x,y); subplot(3,1,3); plot(b*dt,a); yy=cos(3*fliplr(t)); % or use: yy=fliplr(y); z=conv(x,yy); pause; subplot(3,1,3); plot(b*dt,z,'r'); 即在xcorr中不使用scaling。 3. 其他相关问题： 1) 相关程度与相关函数的取值有什么联系？ -------------[转版友gghhjj]------------------------------------------------------------------------------------- 相关系数只是一个比率，不是等单位量度，无什么单位名称，也不是相关的百分数，一般取小数点后两位来表示。 相关系数的正负号只表示相关的方向，绝对值表示相关的程度。因为不是等单位的度量，因而不能说相关系数0.7是0.35两倍，只能说相关系数为0.7的二列变量相关程度比相关系数为0.35的二列变量相关程度更为密切和更高。也不能说相关系数从0.70到0.80与相关系数从0.30到0.40增加的程度一样大。 对于相关系数的大小所表示的意义目前在统计学界尚不一致，但通常按下是这样认为的： 相关系数相关程度 0.00-±0.30 微相关 ±0.30-±0.50 实相关 ±0.50-±0.80 显著相关 ±0.80-±1.00 高度相关 ---------------------------------------------------------------------------------------------------------------------------------------------- 2) 功率，能量，自相关函数的关系： ---[转happy教授]------------------------------------------------------------------------------------------- 参见https://www.wendangku.net/doc/838433499.html,/jingpinke/xhst/final/XiTongJiaoCai/chap6/chap6_3/chap6_3_3.htm 需要指出的是，相关和相关函数的概念原本是为描述随机过程的统计特征而引入的，称之为统计相关函数。按照随机过程的理论，要获得一个实际随机过程的统计相关函数是相当困难的，但对于满足各态历经性(遍历性)或广义平稳的随机过程，它们的统计相关函数等于其一个样本函数的时间相关函数。从确定性信号引出相关的概念，是为后续课程的学习打下一个基础。 两信号互相关函数的傅里叶变换等于其中第一个信号变换与第二个信号变换取共轭二者之乘积，这就是相关定理。对于自相关函数，它的傅里叶变换等于原信号幅度谱的平方。 周期余弦信号和它的自相关函数具有相同的角频率，即周期信号的自相关函数仍然是同周期的周期信号。 在实际应用中，有些信号无法求它的傅里叶变换，但是可以用求自相关函数的方法求得信号的功率谱。

互相关函数自相关函数计算和作图

互相关函数-自相关函数计算和作图

————————————————————————————————作者: ————————————————————————————————日期: ?

互相关函数，自相关函数计算和作图 1.自相关和互相关的概念。 ●互相关函数是描述随机信号ｘ(t）,y(t)在任意两个不同时刻t1，t2间的相关程度。 ●自相关函数是描述随机信号x(t）在任意两个不同时刻t１，ｔ2间的相关程度。 互相关函数是在频域内两个信号是否相关的一个判断指标，把两测点之间信号的互谱与各自的自谱联系了起来。它能用来确定输出信号有多大程度来自输入信号，对修正测量中接入噪声源而产生的误差非常有效。 ---－-－－-------－----－－－--－－－---------－-－------------－---－－--------－----－-－－--－-－--－- 事实上，在图象处理中，自相关和互相关函数的定义如下：设原函数是f(ｔ）,则自相关函数定义为Ｒ(u）=f(t)*f(-ｔ)，其中*表示卷积；设两个函数分别是ｆ（t)和ｇ(t），则互相关函数定义为R（u)=f(t）*g(-t)，它反映的是两个函数在不同的相对位置上互相匹配的程度。 2.利用ｍａtlab中实现这两个相关并用图像显示: 自相关函数：? dt＝.1; t=[０:dt:100];x=ｃos（t); [a,b]=xｃorr(x,'ｕnbiasｅｄ＇); ｐloｔ(b＊dt,ａ） ?

互相关函数：把［ａ,b]＝ｘｃｏrr(x,＇unbｉased');改为[a,b]=ｘｃｏｒr(x,ｙ,'ｕｎｂia ｓed');便可。 ?３. 实现过程: 在Ｍaｔalb中，求解ｘcorr的过程事实上是利用Ｆoｕrier变换中的卷积定理进行的，即R(ｕ)=ｉffｔ(fｆｔ(f）×ｆft(g)),其中×表示乘法，注：此公式仅表示形式计算，并非实际计算所用的公式。当然也可以直接采用卷积进行计算,但是结果会与xcorr的不同。事实上,两者既然有定理保证，那么结果一定是相同的，只是没有用对公式而已。下面是检验两者结果相同的代码:??dt=.1; ｔ=[0:dt:１00];?x=3*ｓｉn（t）;?ｙ=ｃos（3*t)；?subplot(3,１,1); plｏｔ(t，ｘ）； ｓubplｏt(３,1，2);?ｐlot(t,ｙ); [ａ,b]=ｘcoｒｒ(x，y）； sｕbplot(３,１,３);?plot（b*dt,a）;?yｙ=cos(3*fliｐlr(t)); % ｏr ｕsｅ：ｙy=flｉplr(ｙ）; ｚ=ｃonｖ（x，yy); pause; sｕｂｐｌot（３,1,3）; plot(b＊dt,z,'r＇）;??即在xcoｒr中不使用scａling。 ?4. 其他相关问题：?1) 相关程度与相关函数的取值有什么联系？

互相关函数求相位差

互相关函数求相位差 法一、利用互相关函数的性质：对于单频信号而言，时移相当于相移，相关系数从初始值变成最大值的时候，说明相位差也从初始相位差变为零。 法二、利用互相关函数的两同频正弦信号的互相关函数零时刻值与其相位差的余弦值成正比的原理获得相位差。 比较两种方法可知：第二种方法的计算精度较高。可见如果只是简单的求取互相关函数，用

第一种方法即可（直接调用xcorr），但是如果要求取延迟时间，则可以按照互相关的具体公式编写函数！ 具体程序如下： n=512;%设定每周期数据采集点数 T=5;%采样周期数 fen=60;%将度转化为分:1度=60分 hs=360/(2*pi);%弧度转化为度数 t=0:2*pi/(n-1):2*T*pi;%采样数 N=length(t);%采样长度 y1=4*sin(t);%信号1 y2=4*sin(t+pi/(180*6));%信号2 Cc=xcorr(y1);%求互相关函数 %用互相关函数数学表达式求相位差:rm(n)=Rxy(n)/sqrt(Rxx(0)*Ryy(0)) C0=sum(y1.*y2);%y1和y2互相关 A0=sum(y1.*y1);%y1自相关 B0=sum(y2.*y2);%y2自相关 a=sqrt(A0); b=sqrt(B0); zhunquezhi=(pi/(180*6))*hs*fen jiaocha=acos(C0/(a*b))*hs*fen%相位差计算公式 jdwucha=jiaocha-zhunquezhi%绝对误差 xdwucha=((jiaocha-zhunquezhi)/zhunquezhi)*100%相对误差 %用有效值计算比值差 youxiaoy1=sqrt((1/(N-1))*sum(y1.^2)) %计算y1有效值 youxiaoy2=sqrt((1/(N-1))*sum(y2.^2)) %计算y2有效值 bizhicha=abs((youxiaoy1-youxiaoy2)/youxiaoy1)*100 %计算比值差 %作图 m=(-N+1):(N-1); subplot(311); plot(t,y1); grid; subplot(312); plot(t,y2); grid; subplot(313); plot(m,Cc); grid;