用Minitab画出漂亮的正态分布曲线
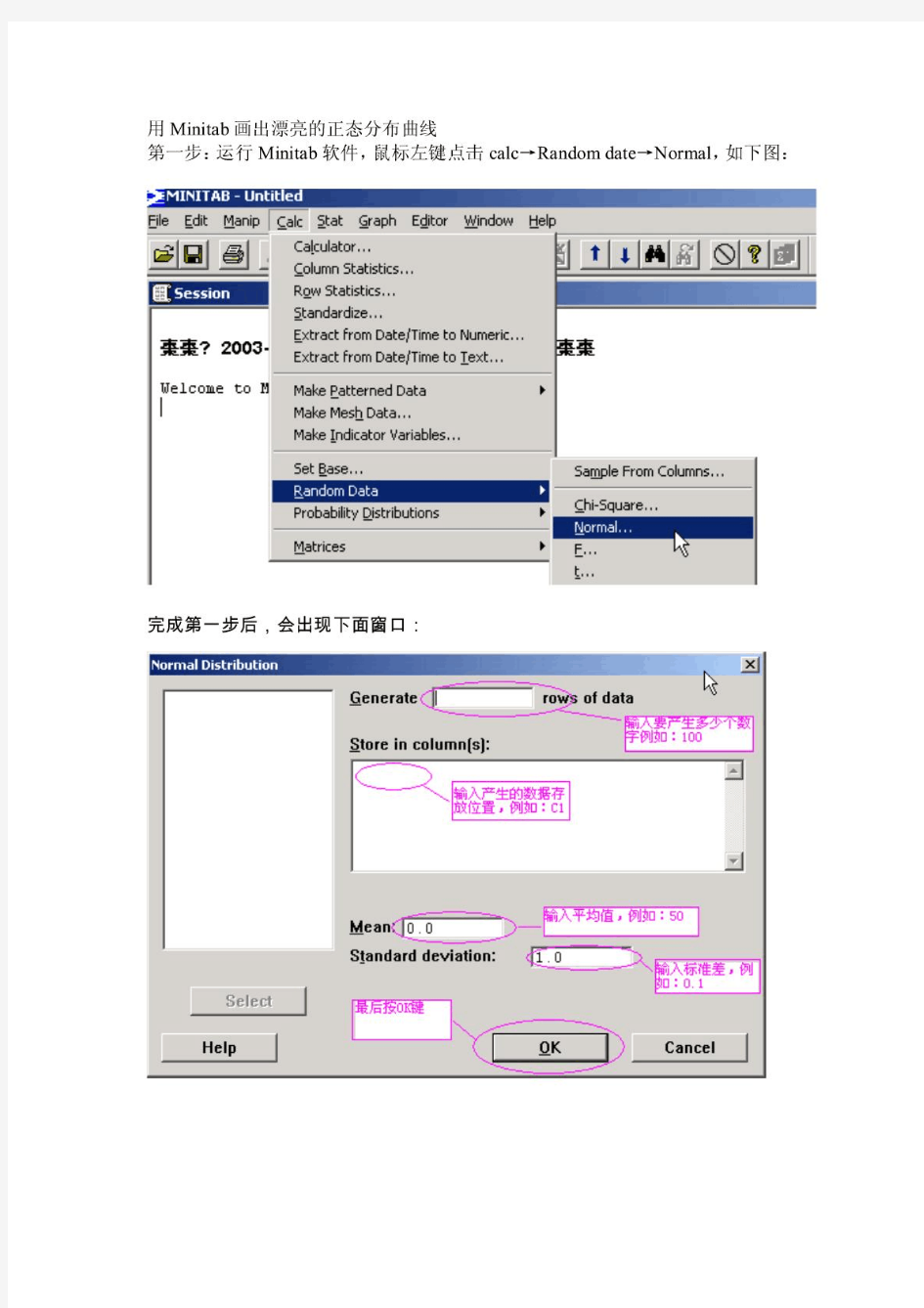

标准正态分布表
标准正态分布表 集团文件发布号:(9816-UATWW-MWUB-WUNN-INNUL-DQQTY-
标准正态分布表
4432198653 1.80.964 1 0.964 8 0.965 6 0.966 4 0.967 2 0.967 8 0.968 6 0.969 3 0.970 0.970 6 1.90.971 3 0.971 9 0.972 6 0.973 2 0.973 8 0.974 4 0.975 0.975 6 0.976 2 0.976 7 20.977 2 0.977 8 0.978 3 0.978 8 0.979 3 0.979 8 0.980 3 0.980 8 0.981 2 0.981 7 2.10.982 1 0.982 6 0.983 0.983 4 0.983 8 0.984 2 0.984 6 0.985 0.985 4 0.985 7 2.20.986 1 0.986 4 0.986 8 0.987 1 0.987 4 0.987 8 0.988 1 0.988 4 0.988 7 0.989 2.30.989 3 0.989 6 0.989 8 0.990 1 0.990 4 0.990 6 0.990 9 0.991 1 0.991 3 0.991 6 2.40.991 8 0.992 0.992 2 0.992 5 0.992 7 0.992 9 0.993 1 0.993 2 0.993 4 0.993 6 2.50.993 8 0.994 0.994 1 0.994 3 0.994 5 0.994 6 0.994 8 0.994 9 0.995 1 0.995 2 2.60.995 3 0.995 5 0.995 6 0.995 7 0.995 9 0.996 0.996 1 0.996 2 0.996 3 0.996 4 2.70.996 5 0.996 6 0.996 7 0.996 8 0.996 9 0.997 0.997 1 0.997 2 0.997 3 0.997 4 2.80.997 4 0.997 5 0.997 6 0.997 7 0.997 7 0.997 8 0.997 9 0.997 9 0.998 0.998 1 2.90.998 1 0.998 2 0.998 2 0.998 3 0.998 4 0.998 4 0.998 5 0.998 5 0.998 6 0.998 6 x00.10.20.30.40.50.60.70.80.9 30.998 7 0.999 0.999 3 0.999 5 0.999 7 0.999 8 0.999 8 0.999 9 0.999 9 1.000 正态分布概率表 Φ( u ) =
t分布和标准规定正态分布
数理统计实验 t分布与标准正态分布 院(系): 班级: 成员:
成员: 成员: 指导老师: 日期:
目录 t分布与标准正态分布的关系 (1) 一、实验目的 (1) 二、实验原理 (1) 三、实验内容及步骤 (1) 四、实验器材 (6) 五、实验结果分析 (6) 六、实验结论 (6)
t分布与标准正态分布的关系 一、实验目的 正态分布是统计中一种很重要的理论分布,是许多统计方法的理论基础。正态分布有两个参数,μ和σ,决定了正态分布的本质。为了应用和计算方便,常将一般的正态变量X通过μ变换[(X-μ)/σ]转化成标准正态变量μ,以使原来各种形态的正态分布都转换为μ=0,σ=1的标准正态分布,亦称μ分布。对于标准正态分布来说,μ是数据整体的平均值,σ是整体的标准差。但实际操作过程中,人们往往难以获得μ和σ。因此人们只能通过样本对这两个参数做出估计,用样本平均值和样本标准差代替整体的平均值和标准差,从而得出了t分布。另外从图像的层面说,正态分布的位置和形态只与μ和σ有关,而t分布不只与样本平均值和样本标准差有关,还与自由度相关。通过实验了解t分布与标准正态分布之间的关系。 二、实验原理 运用EXCEL软件验证t分布与标准正态分布的关系,绘制相应的统计图表进行分析。 三、实验内容及步骤 1.打开Excel文件,将“t分布与标准正态分布N(0,1)”合并并居中,黑体,20字号,红色;
2.选中文件,选项,自定义功能区,加载开发工具.在开发工具中插入滚动条,调节滚动条大小; 3.设置A2单元格格式,数字自定义区”!n=#,##0;[红 色]¥-#,##0”.然后左对齐,设置为红色;
一、标准正态曲线的特点.
一、标准正态曲线的特点: 1)、曲线在z=0位最高点; 2)、曲线以z=0处为中心,双侧对称。 3)、曲线从最高点向左右缓慢下降,并无限延伸,但永不与基线相交。 4)、在正态曲线下中央位置6个标准差内,包含了99.73%的数据。 二、二项试验应当满足以下几个条件: (1) 一次试验只有两种可能结果,即成功与失败。 (2) 各次试验相互独立,几个次试验之间互不影响。 各次试验中成功的概率相等,各次试验中失败的概率自然也相等。 三、1、 解 T=10×Z+50=10×0.4+50=54 学生A 的标准T 分数为54。 四、检验 1、假设:22210:σσ=H 22211:σσ≠H 2、计算检验统计量 F=36.1) 150/(650)146/(746)1/()1/(2222221211≈-?-?=--n n n n x x σσ 3、统计决断 因为,F=1.36
标准正态分布查询表
附表1. 标准正态分布表 x0.000.010.020.030.040.050.060.070.080.09 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.90.500 0 0.539 8 0.579 3 0.617 9 0.655 4 0.691 5 0.725 7 0.758 0 0.788 1 0.815 9 0.841 3 0.864 3 0.884 9 0.903 2 0.919 2 0.933 2 0.945 2 0.955 4 0.964 1 0.971 3 0.977 2 0.982 1 0.986 1 0.989 3 0.991 8 0.993 8 0.995 3 0.996 5 0.997 4 0.998 1 0.504 0 0.543 8 0.583 2 0.621 7 0.659 1 0.695 0 0.729 1 0.761 1 0.791 0 0.818 6 0.843 8 0.866 5 0.886 9 0.904 9 0.920 7 0.934 5 0.946 3 0.956 4 0.964 8 0.971 9 0.977 8 0.982 6 0.986 4 0.989 6 0.992 0 0.994 0 0.995 5 0.996 6 0.997 5 0.998 2 0.508 0 0.547 8 0.587 1 0.625 5 0.662 8 0.698 5 0.732 4 0.764 2 0.793 9 0.821 2 0.846 1 0.868 6 0.888 8 0.906 6 0.922 2 0.935 7 0.947 4 0.957 3 0.965 6 0.972 6 0.978 3 0.983 0 0.986 8 0.989 8 0.992 2 0.994 1 0.995 6 0.996 7 0.997 6 0.998 2 0.512 0 0.551 7 0.591 0 0.629 3 0.666 4 0.701 9 0.735 7 0.767 3 0.796 7 0.823 8 0.848 5 0.870 8 0.890 7 0.908 2 0.923 6 0.937 0 0.948 4 0.958 2 0.966 4 0.973 2 0.978 8 0.983 4 0.987 1 0.990 1 0.992 5 0.994 3 0.995 7 0.996 8 0.997 7 0.998 3 0.516 0 0.555 7 0.594 8 0.633 1 0.670 0 0.705 4 0.738 9 0.770 3 0.799 5 0.826 4 0.850 8 0.872 9 0.892 5 0.909 9 0.925 1 0.938 2 0.949 5 0.959 1 0.967 2 0.973 8 0.979 3 0.983 8 0.987 4 0.990 4 0.992 7 0.994 5 0.995 9 0.996 9 0.997 7 0.998 4 0.519 9 0.559 6 0.598 7 0.636 8 0.673 6 0.708 8 0.742 2 0.773 4 0.802 3 0.828 9 0.853 1 0.874 9 0.894 4 0.911 5 0.926 5 0.939 4 0.950 5 0.959 9 0.967 8 0.974 4 0.979 8 0.984 2 0.987 8 0.990 6 0.992 9 0.994 6 0.996 0 0.997 0 0.997 8 0.998 4 0.523 9 0.563 6 0.602 6 0.640 4 0.677 2 0.712 3 0.745 4 0.776 4 0.805 1 0.835 5 0.855 4 0.877 0 0.896 2 0.913 1 0.927 9 0.940 6 0.951 5 0.960 8 0.968 6 0.975 0 0.980 3 0.984 6 0.988 1 0.990 9 0.993 1 0.994 8 0.996 1 0.997 1 0.997 9 0.998 5 0.527 9 0.567 5 0.606 4 0.644 3 0.680 8 0.715 7 0.748 6 0.779 4 0.807 8 0.834 0 0.857 7 0.879 0 0.898 0 0.914 7 0.929 2 0.941 8 0.952 5 0.961 6 0.969 3 0.975 6 0.980 8 0.985 0 0.988 4 0.991 1 0.993 2 0.994 9 0.996 2 0.997 2 0.997 9 0.998 5 0.531 9 0.571 4 0.610 3 0.648 0 0.684 4 0.719 0 0.751 7 0.782 3 0.810 6 0.836 5 0.859 9 0.881 0 0.899 7 0.916 2 0.930 6 0.943 0 0.953 5 0.962 5 0.970 0 0.976 2 0.981 2 0.985 4 0.988 7 0.991 3 0.993 4 0.995 1 0.996 3 0.997 3 0.998 0 0.998 6 0.535 9 0.575 3 0.614 1 0.651 7 0.687 9 0.722 4 0.754 9 0.785 2 0.813 3 0.838 9 0.862 1 0.883 0 0.901 5 0.917 7 0.931 9 0.944 1 0.953 5 0.963 3 0.970 6 0.976 7 0.981 7 0.985 7 0.989 0 0.991 6 0.993 6 0.995 2 0.996 4 0.997 4 0.998 1 0.998 6 x0.00.10.20.30.40.50.60.70.80.9 30.998 70.999 00.999 30.999 50.999 70.999 80.999 80.999 90.999 9 1.000 0
正态分布讲解(含标准表)
2.4正态分布 复习引入: 总体密度曲线:样本容量越大,所分组数越多,各组的频率就越接近于总体在相应各组取值的概率.设想样本容量无限增大,分组的组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线,这条曲线叫做总体密度曲线. 总体密度曲线 b 单位 O 频率/组距 a 它反映了总体在各个范围内取值的概率.根据这条曲线,可求出总体在区间(a,b)内取值的概率等于总体密度曲线,直线x=a,x=b及x轴所围图形的面积. 观察总体密度曲线的形状,它具有“两头低,中间高,左右对称”的特征,具有这种特征的总体密度曲线一般可用下面函数的图象来表示或近似表示: 2 2 () 2 , 1 (),(,) 2 x x e x μ σ μσ ? πσ - - =∈-∞+∞ 式中的实数μ、)0 (> σ σ是参数,分别表示总体的平均数与标准差,, ()x μσ ? 的图象为正态分布密度曲线,简称正态曲线. 讲解新课:
一般地,如果对于任何实数a b <,随机变量X 满足 ,()()b a P a X B x dx μσ?<≤=?, 则称 X 的分布为正态分布(normal distribution ) .正态分布完全由参数μ和σ确定,因此正态分布常记作),(2 σ μN .如果随机变量 X 服从正态分布,则记为X ~),(2σμN . 经验表明,一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似服从正态分布.例如,高尔顿板试验中,小球在下落过程中要与众多小木块发生碰撞,每次碰撞的结果使得小球随机地向左或向右下落,因此小球第1次与高尔顿板底部接触时的坐标 X 是众多随机碰撞的结果,所以它近似服从正态分布.在现实生活中,很多随机变量都服从或近似地服从正态分布.例如长度测量误差;某一地区同年龄人群的身高、体重、肺活量等;一定条件下生长的小麦的株高、穗长、单位面积产量等;正常生产条件下各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命等);某地每年七月份的平均气温、平均湿度、降雨量等;一般都服从正态分布.因此,正态分布广泛存在于自然现象、生产和生活实际之中.正态分布在概率和统计中占有重要的地位. 说明:1参数μ是反映随机变量取值的平均水平的特征数,可以用样本均值去佑计;σ是衡量随机变量总体波动大小的特征数,可以用样本标准差去估计. 2.早在 1733 年,法国数学家棣莫弗就用n !的近似公式得到了正态分布.之后,德国数学家高斯在研究测量误差时从另一个角度导出了它,并研究了它的性质,因此,人们也称正态分布为高斯分布. 2.正态分布),(2 σ μN )是由均值μ和标准差σ唯一决定的分布 通过固定其中一个值,讨论均值与标准差对于正态曲线的影响
正态曲线
正态曲线主要内涵
主要内涵 在联系自然、社会和思维的实践背景下,我们以正态分布的本质为基础,以正态分布曲 线及面积分布图为表征 (以后谈及正态分布及正态分布论就要浮现此图) 进行抽象与提升, , 抓住其中的主要哲学内涵,归纳正态分布论(正态哲学)的主要内涵如下: 整体论 正态分布启示我们,要用整体的观点来看事物。“系统的整体观念或总体观念是系统概 念的精髓。” 正态分布曲线及面积分布图由基区、负区、正区三个区组成,各区比重不一样。 用整体来看事物才能看清楚事物的本来面貌, 才能得出事物的根本特性。 不能只见树木不见 森林,也不能以偏概全。此外整体大于部分之和,在分析各部分、各层次的基础上,还要从 整体看事物, 这是因为整体有不同于各部分的特点。 用整体观来看世界, 就是要立足在基区, 放眼负区和正区。要看到主要方面,还要看到次要方面,既要看到积极的方面还要看到事物 消极的一面, 看到事物前进的一面还要看到落后的一面。 片面看事物必然看到的是偏态或者 是变态的事物,不是真实的事物本身。 重点论 正态分布曲线及面积分布图非常清晰的展示了重点,那就是基区占 68.27%,是主体, 要重点抓,此外 95%,99%则展示了正态的全面性。认识世界和改造世界一定要住住重点, 因为重点就是事物的主要矛盾,它对事物的发展起主要的、支配性的作用。抓住了重点才能 一举其纲,万目皆张。事物和现象纷繁复杂,在千头万绪中不抓住主要矛盾,就会陷入无限 琐碎之中。由于我们时间和精力的相对有限性,出于效率的追求,我们更应该抓住重点。在 正态分布中,基区占了主体和重点。如果我们结合 20/80 法则,我们更可以大胆的把正区也 可以看做是重点。 发展论 联系和发展是事物发展变化的基本规律。任何事物都有其产生、发展和灭亡的历史,如 果我们把正态分布看做是任何一个系统或者事物的发展过程的话, 我们明显的看到这个过程 经历着从负区到基区再到正区的过程。 无论是自然、 社会还是人类的思维都明显的遵循这这 样一个过程。准确的把握事物或者事件所处的历史过程和阶段极大的有助于掌握我们对事 物、事件的特征和性质,是我们分析问题,采取对策和解决问题的重要基础和依据。发展的 阶段不同,性质和特征也不同,分析和解决问题的办法要与此相适应,这就是具体问题具体 分析,也是解放思想、实事求是、与时俱乐进的精髓。正态发展的特点还启示我们,事物发 展大都是渐进的和累积的,走渐进发展的道路是事物发展的常态。例如,遗传是常态,变异 是非常态。 总之,正态分布论是科学的世界观,也是科学的方法论,是我们认识和改造世界的最重 要和最根本的工具之一,对我们的理论和实践有重要的指导意义。以正态哲学认识世界,能 更好的认识和把握世界的本质和规律, 以正态哲学来改造世界, 能更好的在尊重和利用客观 规律,更有效的改造世界。
正态分布的概念和特征
第一节正态分布的概念和特征 一、正态分布的概念 由表的频数表资料所绘制的直方图,图(1)可以看出,高峰位于中部,左右两侧大致对称。我们设想,如果观察例数逐渐增多,组段不断分细,直方图顶端的连线就会逐渐形成一条高峰位于中央(均数所在处),两侧逐渐降低且左右对称,不与横轴相交的光滑曲线图(3)。这条曲线称为频数曲线或频率曲线,近似于数学上的正态分布(normal distribution)。由于频率的总和为100%或1,故该曲线下横轴上的面积为100%或1。 图频数分布逐渐接近正态分布示意图 为了应用方便,常对正态分布变量X作变量变换。 ()
该变换使原来的正态分布转化为标准正态分布 (standard normal distribution),亦称u分布。u被称为标准正态变量或标准正态离差(standard normal deviate)。 二、正态分布的特征: 1.正态曲线(normal curve)在横轴上方均数处最高。 2.正态分布以均数为中心,左右对称。 3.正态分布有两个参数,即均数和标准差。是位置参数,当固定不变时,越大,曲线沿横轴越向右移动;反之,越小,则曲线沿横轴越向左移动。 是形状参数,当固定不变时,越大,曲线越平阔;越小,曲线越尖峭。通常用表示均数为,方差为的正态分布。用N(0,1)表示标准正态分布。 4.正态曲线下面积的分布有一定规律。 实际工作中,常需要了解正态曲线下横轴上某一区间的面积占总面积的百分数,以便估计该区间的例数占总例数的百分数(频数分布)或观察值落在该区间的概率。正态曲线下一定区间的面积可以通过附表1求得。对于正态或近似正态分布的资料,已知均数和标准差,就可对其频数分布作出概约估计。 查附表1应注意:①表中曲线下面积为-∞到u的左侧累计面积;②当已知μ、σ和X时先按式()求得u值,再查表,当μ、σ未知且样本含量n足够大时,可用样本均数和标准差S分别代替μ和σ,按式求得u值,再查表;③曲线下对称于0的区间面积相等,如区间(-∞,)与区间(,∞)的面积相等,④曲线下横轴上的总面积为100%或1。
标准正态分布表
标准正态分布表 标准正态分布表怎么看 将未知量Z对应的列上的数与行所对应的数字结合查表定位 例如要查Z=1.96的标准正态分布表 首先在Z下面对应的数找到1.9 然后在Z右边的行中找到6 这两个数所对应的值为0.9750 即为所查的值 有谁知道,为什么标准正态分布表x的右边和下边都有值啊,难道一个x可以有两个值,看表是怎么看啊 那是一个精度问题,例如当x=0.12,那么应该先在x下方找到0.1,再在右边找到0.02,那么这两个同时对应的那个数就应该是你所要的! 标准正态分布的x值算出来介于两个之间,取哪一个。概论值如果介于两个间,取更大的还是更近的啊 精度要求不是很高的话,在正中取中间值,靠一边取更近的,四舍五入。 精度要求高的话用插值函数,比如在两点间作一次函数逼近。 为什么u0.025等于1.96?标准正态分布表查不到这个结果啊。u0.05是多少?u0.1是多少? 因为P{Z<1.96}=1-0.025=0.975 u0.05=1.645 因为P{Z<1.645}=1-0.05 u0.1类似 统计学中,标准正态分布表中Z值代表意义 Z值只是一个临界值,他是标准化的结果,本身没有意义,有意义的在于在标准正态分布模型中它代表的概率值。通过查表便可以知道。 标准正态分布 期望值μ=0,即曲线图象对称轴为Y轴,标准差σ=1条件下的正态分布,记为N(0,1)。 标准正态分布又称为u分布,是以0为均数、以1为标准差的正态分布,记为N(0,1)。 标准正态分布的密度函数为:
标准正态分布曲线下面积分布规律是:在-1.96~+1.96范围内曲线下的面积等于0.9500,在-2.58~+2.58范围内曲线下面积为0.9900。统计学家还制定了一张统计用表(自由度为∞时),借助该表就可以估计出某些特殊u1和u2值范围内的曲线下面积。
标准正态分布函数表
标准正态分布: 标准正态分布(英语:standard normal distribution,德语Standardnormalverteilung),是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。期望值μ=0,即曲线图象对称轴为Y轴,标准差σ=1条件下的正态分布,记为N(0,1)。 定义: 标准正态分布又称为u分布,是以0为均数、以1为标准差的正态分布,记为N(0,1)。 标准正态分布曲线下面积分布规律是:在-1.96~+1.96范围内曲线下的面积等于0.9500,在-2.58~+2.58范围内曲线下面积为0.9900。统计学家还制定了一张统计用表(自由度为∞时),借助该表就可以估计出某些特殊u1和u2值范围内的曲线下面积。 正态分布的概率密度函数曲线呈钟形,因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是位置参数均数为0, 尺度参数:标准差为1的正态分布(见下图中绿色曲线)。 特点: 密度函数关于平均值对称 平均值与它的众数(statistical mode)以及中位数(median)同一数值。 函数曲线下68.268949%的面积在平均数左右的一个标准差范围内。
95.449974%的面积在平均数左右两个标准差的范围内。 99.730020%的面积在平均数左右三个标准差的范围内。 99.993666%的面积在平均数左右四个标准差的范围内。 函数曲线的反曲点(inflection point)为离平均数一个标准差距离的位置。 标准偏差: 深蓝色区域是距平均值小于一个标准差之内的数值范围。在正态分布中,此范围所占比率为全部数值之68%,根据正态分布,两个标准差之内的比率合起来为95%;三个标准差之内的比率合起来为99%。 在实际应用上,常考虑一组数据具有近似于正态分布的概率分布。若其假设正确,则约68.3%数值分布在距离平均值有1个标准差之内的范围,约95.4%数值分布在距离平均值有2个标准差之内的范围,以及约99.7%数值分布在距离平均值有3个标准差之内的范围。称为“68-95-99.7法则”或“经验法则”。
标准正态曲线下面积的求法
.标准正态曲线下面积的求法(查表资料1-3) 1.已知Z值求概率 ⑴.求Z=0至某一Z值之间的概率:直接查表 ⑵.求两个Z值之间的概率 ?两Z值符号相同:PZ1-Z2=PZ2-PZ1 ? ?两Z值符号相反:PZ1-Z2=PZ2+PZ1 ? ⑶.求某一Z值以上的概率 ?Z>0时,PZ-∞=0.5-PZ ? ?Z<0时,PZ-∞=0.5+PZ ? ⑷.求某一Z值以下的概率 ?Z>0时,P-∞-Z=0.5+PZ ? ?Z<0时,P-∞-Z=0.5-PZ ? 2.已知面积(概率)求Z值 ⑴.求Z=0以上或以下某一面积对应的Z值:直接查表 ⑵.求与正态曲线上端或下端某一面积P相对应的Z值:先用0.5-PZ,再查表 ⑶.求与正态曲线下中央部位某一面积相对应的Z值:先计算P/2,再查表 3.已知概率P或Z值,求概率密度Y ?直接查正态分布表就能得到相应的概率密度Y值。 ? ?如果由概率P求Y值,要注意区分已知概率是位于正态曲线的中间部分,还是两尾端部分,才能通过查表求得正确的概率密度。
(1)已知Z值求面积 如果是原始数据,要首先转化为标准分数,然后再由Z值查到面积,具体做法有以下三种: 第一种情况:求Z=0至某一Z值之间的面积。可以直接查表(附表1); 如查Z=0到Z=0.50的面积。查得P=0.19146。 再如:求Z=0到Z=2之间的面积。可以直接查。查附表1。先找Z行,找到2这个值;再看P行,在2旁边的那个P值为0.47725。从而得到从Z=0到Z=2这个区域的面积为0.47725。 第二种情况:求两个Z值之间的面积; 首先要找出这两个值到Z=0的面积找出来,然后看它们的符号相同还是相反。如果相同,就用大的面积减去小的面积所得差即为所求;如果符号相反,就把两个面积加起来,所得和即为所求面积。 例如:要求Z=0.50到Z=2之间的面积。先查得Z=0到Z=0.50的面积,结果查得0.19146;在查得Z=0到Z=2之间的面积,结果查得0.47725。然后看两个Z值的符号是相同还是相同。结果发现相同。那么最终所求面积等于0.47725减去0.19146,结果得0.28579。即从Z=0.50累积到Z=2的概率为0.28579,或所求面积为0.28579。 又如:要求Z=-1.50到Z=1之间的面积。先查得Z=0到Z=-1.50的面积,结果查得0.43319;在查得Z=0到Z=1之间的面积,结果查得0.34134。然后看两个Z值的符号是相同还是相反。结果发现相同。 那么最终所求面积等于0.43319加上0.34134,结果得0.77633。即从Z=-1.50累积到Z=1的概率为 0.77633,或所求面积为0.77633。 第三种情况:求某一Z值以上或以下的面积。即左端或右端,上端或下端。 例如:求Z=2以上的面积。先查Z=0到Z=2的面积为多少,查附表1的0.47725,则Z=2以上的面积就等于半块面积减去0.47725。这时就用到标准正态曲线的对称性。即整个面积为1,则半个面积为 0.50。所以Z=2以上的面积为0.02275。同理根据对称性可以求得Z=2以下的面积,Z=-2以上或以下 的面积。 例如:某地区某年高考英语这一科的考生有46000人,经过计算平均分为56.03,标准差为19.06,假定这个分布是正态的,现在问成绩在90分以上的有多少人,60分到90分有多少人,60分以下的有多少人。 (2)已知面积求Z值 第一种情况:求Z=0以上或以下某一面积相对应的Z值; 求Z=0至某一Z值之间面积所对应的Z值。可以直接查表(附表1)。如已知Z=0往上的面积等于0.30,求所对应的Z值。先查P行,找到0.30。当然表中不一定有该数据,可以找最接近的数,其所对应的Z值就是我们所要求的。查得Z=0.84。所以从Z=0往上0.30的面积所对应的Z值为0.84。同理可得从Z=0往下的面积对应的Z值,不过要在所求得的Z值前加一个负号。
标准正态曲线下的面积表
标准正态曲线下的面积表 0.0 .0000 .0040 .0080 .0120 .0160 .0199 .0239 .0276 .0319 .0359 0.1 .0398 .0438 .0478 .0517 .0557 .0596 .0636 .0675 .0714 .0754 0.2 .0793 .0832 .0871 .0910 .0948 .0987 .1026 .1064 .1103 .1141 0.3 .1179 .1217 .1255 .1293 .1331 .1368 .1406 .1443 .1480 .1517 0.4 .1554 .1591 .1628 .1664 .1700 .1736 .1772 .1808 .1844 .1879 0.5 .1915 .1950 .1985 .2019 .2054 .2088 .2123 .2157 .2190 .2224 0.6 .2258 .2291 .2324 .2357 .2389 .2422 .2454 .2486 .2518 .2549 0.7 .2580 .2612 .2642 .2673 .2704 .2734 .2764 .2794 .2823 .2852 0.8 .2881 .2910 .2939 .2967 .2996 .3023 .3051 .3078 .3106 .3133 0.9 .3159 .3186 .3212 .3238 .3264 .3289 .3316 .3340 .3365 .3389 1.0 .3413 .3438 .3461 .3485 .3508 .3531 .3554 .3577 .3599 .3621 1.1 .3643 .3665 .3686 .3708 .3729 .3749 .3770 .3790 .3810 .3830 1.2 .3849 .3869 .3888 .3907 .3925 .3944 .3962 .3980 .3997 .4015 1.3 .4032 .4049 .4066 .4082 .4099 .4115 .4131 .4147 .4162 .4177 1.4 .4192 .4207 .4222 .4236 .4251 .4265 .4270 .4292 .4306 .4319 1.5 .4332 .4345 .4357 .4370 .4382 .4394 .4406 .4418 .4429 .4441 1.6 .4452 .4463 .4474 .4484 .4495 .4505 .4515 .4525 .4535 .4545 1.7 .4554 .4564 .4573 .4582 .4591 .4599 .4608 .4616 .4625 .4633 1.8 .4641 .4649 .4656 .4664 .4671 .4678 .4686 .4693 .4699 .4706 1.9 .4713 .4719 .4726 .4732 .4733 .4744 .4750 .4756 .4761 .4767 2.0 .4772 .4778 .4783 .4788 .4793 .4798 .4803 .4808 .4812 .4817
标准正态分布表
? 标准正态分布表 φ( - x ) = 1 –φ( x )(请暂时忽略此公式)t x 0 / 【 0 0 0 0 0 9 9 9 、 9 9 8 8 8 7 7 : 6 6 5 4 3 3 2 、 1 0 8 7 6 4 3 1 , 9 7 5 3 1 8 4 … 3 0 7 4 1 8 4 — 6 2 8 4 9 5 > 0 5 9 4 8 3 7 0 > 4 7 1 4 7 9 2 ! 4 6 7 9 0 1 2 — 3 3 4 4 4 3 2》 1 0 9 7 5 3 1 8 | 6 3 9 6 2 8 4 ~ 9 5 0 5 9 1 3 8 * 1 5 8 1 4 7 9 1 @ 3 5 6 8 9 9 0 … 0 0 9 9 8 7 、 5 4 2 0 7 5 2 " 9 6 2 9 5 1 7 2 … 7 2 7 2 6 1 5 } 9 2 6 9 2 5 7@ 2 4 6 8 0 1
0¥ 2 3 4 4 5 5 5 5 \ 5 5 4 4 3 2 1 — 9 8 6 5 3 1 8 ( 6 4 2 8 6 3 0 6 $ 3 9 6 2 8 4 0 & 6 2 7 2 2 8 3 8 " 3 8 3 8 2 7 1 ! 6 0 4 8 2 6 0 4 、 7 1 4 8 1 4 8 ~ 1 4 7 0 3 6 8 、 1 4 6 9 1 3 6 ] 8 0 2 5 7 9 1 2 ? 4 6 8 0 1 3 5 ! 6 8 9 1 2 3 5 < 6 7 9 0 1 2 3 4 , 5 6 7 8 9 0 1 - 2 3 4 4 5 6 7 { 7 8 9 9 0 1 1 2 2 3 4 4 5 5 6 6 x0 3 7 0 3 5 7 8 8 9 9 0就是F(t) 正态分布概率表 Φ( u ) =
