运筹学作业题整理

运筹学作业整理
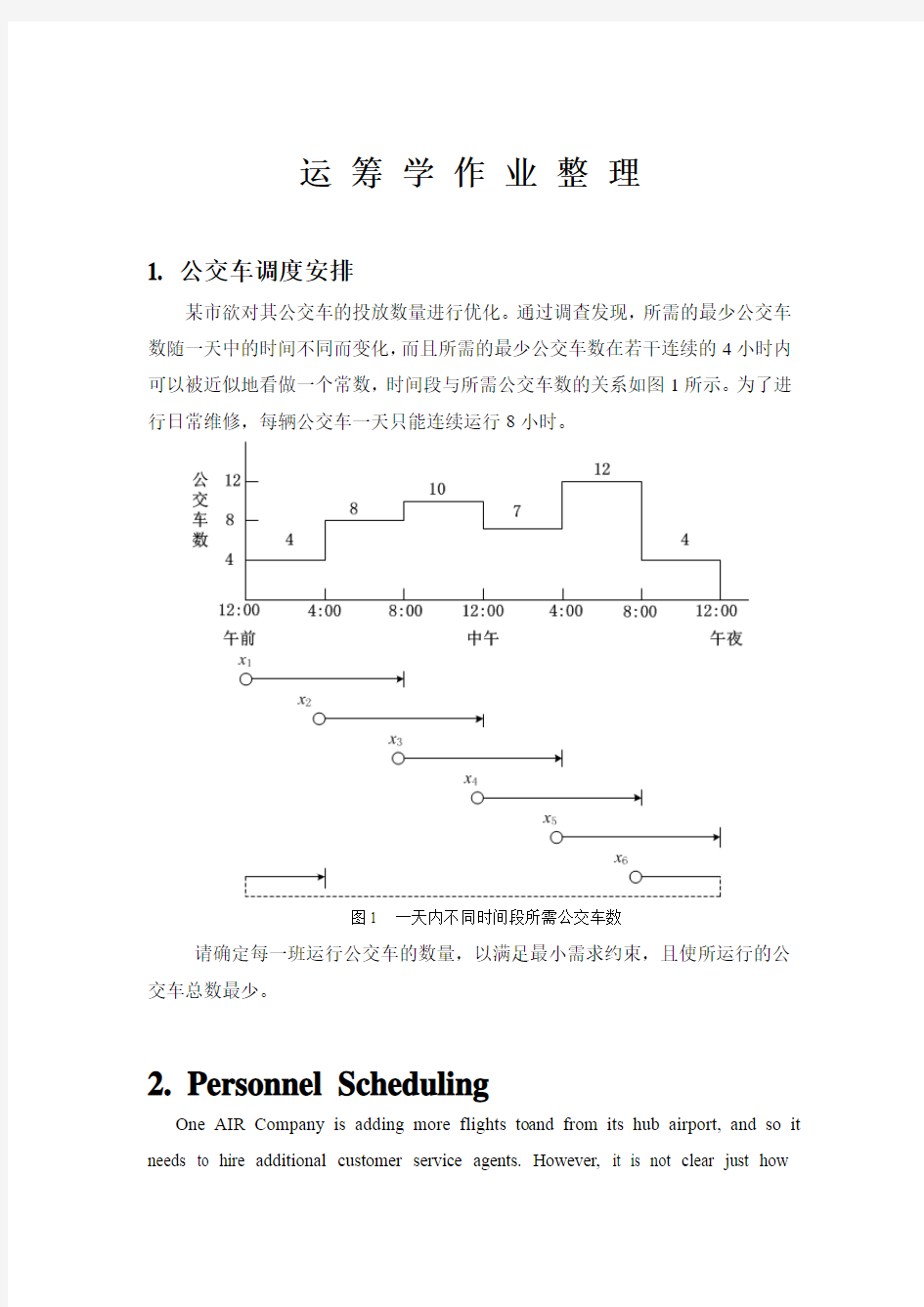
1. 公交车调度安排
某市欲对其公交车的投放数量进行优化。通过调查发现,所需的最少公交车数随一天中的时间不同而变化,而且所需的最少公交车数在若干连续的4小时内可以被近似地看做一个常数,时间段与所需公交车数的关系如图1所示。为了进行日常维修,每辆公交车一天只能连续运行8小时。
图1 一天内不同时间段所需公交车数
请确定每一班运行公交车的数量,以满足最小需求约束,且使所运行的公交车总数最少。
2. Personnel Scheduling
One AIR Company is adding more flights to and from its hub airport, and so it needs to hire additional customer service agents. However, it is not clear just how
many more should be hired. Management recognizes the need for cost control while also consistently providing a satisfactory level of service to customers. Therefore, an OR team is studying how to scheduling the agents to provide satisfactory service with the smallest personnel cost.
Based on the new schedule of flights, an analysis has been made of the minimum number of customer service agents that need to be on duty at different times of the day to provide a satisfactory level of service. The right most column of the flowing table shows the number agents needs for the time periods given in the first column. The other entries in this table reflect one of the provisions in the company’s current contract with the union that the represents the customer service agents. The provision is that each agent works an 8-hour shift 5 days per week.
The five authorized eight-hour shifts are
–Shift 1: 6:00 AM to 2:00 PM
–Shift 2: 8:00 AM to 4:00 PM
–Shift 3: Noon to 8:00 PM
–Shift 4: 4:00 PM to midnight
-Shift 5: 10:00 PM to 6:00 AM.
How many agents should be assigned to each shift? Please set up a LP model and solve it.
3.已知某工厂计划生产I,II,III三种产品,各产品需要在A,B,C 设备上加工,有关数据见表4-24。
表4-24
产品设备I II III
设备有效台
时(月)
A 8 2 10 300
B 10 5 8 400
C 2 13 10 420
单位产品利润
(千元)
3 2 2.9
请回答:
(1)如何发挥设备能力,使生产盈利最大?
(2)若为了增加产量,可借用其他工厂的设备B,每月可借用60台时,租金为1.8万元,是否划算?
(3)若另有两种新产品IV,V,其中IV需用A设备12台时,B设备5台时,C设备10台时,单位产品盈利2.1千元;新产品V 需用A设备4台时,B设备4台时,C设备12台时,单位产品盈利1.87千元。且A,B,C设备台时不增加,生产这两种新产品是否划算?
(4)对产品工艺重新进行设计,改进构造。改进后生产每件产品I,需用A设备9台时,B设备12台时,C设备4台时,单位产品盈利4.5千元,这对原计划有何影响?
4.求下述线性规划问题目标函数的上界和下界。
5. 下表为用单纯形法计算时某一步的表格,已知该线性规划的目标函数为max z=5x1+3x2,约束形式为≤,x3和x4为松弛变量,表中解代入目标函数后得z=10。
x1x2x3x4
x3 c 0 1 1/5 2
x1 d e 0 1 a
c j-z j b -1 f g
1. 求a,b,c,d,e,f,g的值;
2. 表中给出的解是否为最优解。
6. 分析下列参数规划中当0
θ≤时最优解的变化情况。
θ≥和0
7. 分析下列参数规划中当0
θ≤时最优解的变化情况
θ≥和0
8. 消防车调度问题
某市消防中心同时接到了三处火警报告。根据当前的火势,三处火警地点分别需要2辆、2辆和3辆消防车前往灭火。三处火警地点的损失将依赖于消防车到达的及时程度:记t ij为第j辆消防车到达火警地点i的时间(分钟),则三处火警地点的损失分别为:
6t11+4t12,7t21+3t22,9t31+8t32+5t33;
目前可供消防中心调度的消防车正好有7辆,分别属于三个消防站(可用消防车数量分别为3辆、2辆、2辆)。消防车从三个消防站到三个火警地点所需要的时间如表1所示。该公司应如何调度消防车,才能使总损失最小?
表1 消防站到三个火警地点所需要的时间
时间(分钟) 火警地点1
火警地点2
火警地点3
消防站1 6 7 9 消防站2 5 8 11 消防站3
6
9
10
如果三处火警地点的损失分别为:
4t 11+6t 12,3t 21+7t 22,5t 31+8t 32+9t 33,
调度方案是否需要改变?
9. 蔬菜供应方案:
某城市为人口不到20万的小城市,根据该市蔬菜种植情况,分别在A 、B 、C 设3个收购点。清晨4点前菜农将蔬菜运至各收购点,再由各收购点分别送到全市8个菜市场。该市道路情况、各路段距离(单位:100米)及各收购点、菜市场的具体位置如下图所示。
⑥
①5A
4
7
87②
3
6
B
T 4
7
11
5
④
6
10
11
⑧
⑦
510
86
67
75T 2
T 3⑤
53
③
4
4
8
7
5T 1
6
C
按统计数据,A 、B 、C 3个收购点每天收购量分别为200、170、160(单位:100千克),各菜市场每天的需求量以及发生供应短缺时的损失(单位:元/100千克)见表1.
表1 各菜市场日需求量及短期损失费用信息表菜市场①②③④⑤⑥⑦⑧日需求/千克75 60 80 70 100 55 90 80 短缺损失 /(元
10 8 5 10 10 8 5 8 /100千克)
设从收购点至各菜市场蔬菜调运费用为1元(100千克·100米),试解决如下问题:
(1)为该市设计一个从各收购点至各菜市场的定点供应方案,使得蔬菜调运及预期的短缺损失最小;
(2)若规定各菜市场短缺量一律尽量不超过需求量的20%,重新设计定点供应方案;
(3)为满足居民的蔬菜供应,该市规划增加蔬菜种植面积,那么增产的蔬菜每天应分别向A、B、C3个采购点各供应多少最经济合理?
10.具有截止时间和误时惩罚的任务安排问题可描述如下:
(1)给定n个任务的集合S={1,2,……,n};
(2)完成任务i需要ti时间,1<=i<=n;
(3)任务i的截止时间为di,1<=i<=n,即要求任务i在时间di 之前结束;
(4)任务i的误时惩罚为wi,1<=i<=n,即任务i未在时间di 之前结束将招致wi的惩罚;若按时完成,则无惩罚。
任务安排问题要求确定S的一个时间表(最优时间表)使得总误时惩罚达到最小。
任务i作业
1211113时间
期限di4243146
罚款wi70605040302080
11.一个单位时间任务是指恰好需要一个单位时间完成的任务。给定一个单位时间任务有限集S,对S的一个调度即S的一个排列,其中规定了这些任务的执行顺序. 该调度中的第一个任务开始于时间0,结束于时1;第二个任务开始于时间1,结束于时间2,……
单处理器上具有截止期限和误工惩罚的单位时间任务调度问题的输入如下:
1. 包含n个单位时间任务的集合S={1,2,……,n};
2. 截止期限d1 ,……,dn ,(1≤d,≤n),任务i要求在di前完成;
3. n个非负的权(误工惩罚)w1 ,……,wn .如果任务i没在时间di 之前结束,则导致罚款wi ;
要求找出S的一个调度,使之最小化总的惩罚
12.装箱问题描述
有无限多个箱子,每个箱子容量为V,有N件物品,每件体积分别为v1,v2 ,…,vn (0< vi≤V),求能容纳这个N件物品的最少箱数。
13.树枝形专用线非直达车流取送车问题
13.1、设定条件
(1)一台调车机车作业,连送带取; (2)每专用线至少有两条股道(见下图); (3)各专用线待送、待取车数已定; (4)各段距离和走行时间已知。 13.2、优化目标
(1)使机车取送总时间F1最小;
(2)在F1最小的基础上,使所有专用线总的入线车小时消耗F2最小。
(3)在F1最小的基础上,使总的走行车辆公里数F3最小。 13.3、求合理的取送顺序,使目标实现。
图中顶点和边的意义:
树根——车站;树枝——走行线;树叶——专用线; 分枝点——道岔;共用枝——连接两个分枝点的边; -号代表送车,+号代表取车。
10 4.5
5
2.0 6 2.5 4
1.5 12 3.0 9
2.0
15
4.0
10
2.5
8 2.0 7
1.5
V 0
V 1 V 2
V 3
V 4 V 5 V 6 V 7 V 8 V 9
V 10 V 11 23-?? ?
+??
14-??
?+??
62-??
?+??
51-??
?+??75-?? ?+??
38-??
?+??
5 2.0
14.某工程各项工作间的逻辑关系如下表所示,试绘制双代号网络图,并计算各项工作的时间参数,判定关键线路。
工作名称前导工作后续工作持续时间
A ——C、D 2
B ——E、G 3
C A J 5
D A F 3
E B
F 2
F D、E H、I 4
G B —— 2
H F J 1
I F —— 3
J C、H —— 4
15.发现的奇异现象:
在上述经典的统筹网络图中加入下列时间约束:
1. “A工序结束后至少10天,B工序才能结束”——结束-结束型最小时间约束;
2. “B工序开始后至少8天,C工序才能开始”——开始-开始型最小时间约束。计算出时间参数,求出关键路线。
16.马尔科夫链:
Starting from state 2, the probability of absorption into state 0 (A losing all his money) can be obtained by
The probability of A winning $4 (B going broke) ?
0010002020103030204040
1
21
33
21
33
21
33
f f f f f f f f f f f =???=+???=+???=+??=?
?
17. 马尔科夫链:
Customers who are fully paid (in state 0) and then subsequently fall into arrears on new purchases are viewed as “new ” customers who start in state 1.
18.
物资调运问题:
某种物资存放三个仓库 里,存放量分别为 (单位:t);现要将这些物资运往四个销售点 .其需要量分别为 且 ,
已知 到
的距离和单位运价123,,,A A A 123,,a a a 1234,,
,B B B B 1234,,,b b b b 34i j i
j
a b =∑∑i A j B
分别为 (km)和 (元),现要决定如何调运多少,才能使总的吨公
里数和总运费都尽量少?
解: 设变量 表示由 运往 的货物数,于是总吨公里数为 ,总运费为 .
ij d ij c ,1,2,3;1,2,3,4ij x i j ==i A j B 11
ij ij i j d x
==∑∑11ij ij i j c x
==∑∑3411
341141
3
1min min ..
,1,2,3,1,2,3,40,1,2,3;1,2,3,4
ij ij
i j ij ij i j ij i i ij j i ij d x c x s t x a i x b j x i j ======?
?
?
?
?
?
??
==???==??≥==??∑∑∑∑∑∑
运筹学计算题
2.10答案 解:设123,,x x x 分别为甲糖果中,,A B C 的成分;456,,x x x 分别为乙糖果中,,A B C 的成分; 789,,x x x 分别为丙糖果中,,A B C 的成分。根据题意,有: ()() ()()()()1234567891472583691123 31234 4566 456 9 789 147 max (3.400.50)(2.850.40)(2.250.30) 2.001.50 1.000.60.20.150.6s.t. 0.5200z x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x =-?+++-?+++-?++-?++-?++-?++≥++≤++≥++≤++≤++++≤2583690250012000,1,2,,9i x x x x x x x i ? ??? ???? ??? ??? ???++≤?? ++≤??≥=?? 简化得, ()()()()() 1234 56789 112331234 45664569789147258369max 0.9 1.4 1.90.450.95 1.450.050.450.950.60.20.150.60.5s.t. 2000250012000,1,2,,9i z x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x i =+++++-++≥++?? ≤++?≥++≤++≤++?++≤++≤++≤≥= ????? ?? ??? ??? 5.3答案
运筹学考试练习题(天津大学)
07级工管运筹学期末习题课 一、考虑线性规划问题(P )max 0 z CX AX b X ==?? ≥? (1) 若12,X X 均为(P )的可行解,[0,1]λ∈,证明12(1)X X λλ+-也是(P ) 的可行解; (2) 写出(P )的对偶模型(仍用矩阵式表示)。 二、有三个线性规划: (Ⅰ) [Min] z =CX (Ⅱ) [Min] z =CX (Ⅲ) [Min] z =CX 约束条件AX =b 约束条件AX =b 约束条件AX =b X 0 X 0 X 0 已知 X 是(Ⅰ)的最优解,X 是(Ⅱ)的最优解,X *是(Ⅲ)的最优解,Y 是(Ⅰ)的对偶问题的最优解, 试证:(1)()()'-'-≤**C C X X 0; (2) C X X Y b b ()()***-≤-。 三、已知线性规划问题 ?? ? ??=≥+=++++=++++++++=)5,,1(03.00)(max 2 253232221212 143132121115 43322111Λj x t b x x a x a x a t b x x a x a x a st x x x c x c x t c z j 当1t =2t =0时,用单纯形法求得最终表如下: 要求:1. 确定23222113121121321,,,,,,,,,,a a a a a a b b c c c 的值; 2. 当2t =0时,1t 在什么范围内变化上述最优解不变; 3. 当1t =0时,2t 在什么范围内变化上述最优基不变。 1x 2x 3x 4x 5x 3x 5/2 0 1/2 1 1/2 0 1x 5/2 1 -1/2 0 -1/6 1/3 j j z c - -4 -4 -2
运筹学作业3(第二章部分习题)答案
运筹学作业2(第二章部分习题)答案 2.4 给出线性规划问题 123412341234min 2356232.. 2330,1,2,3,4 j z x x x x x x x x s t x x x x x j =+++?+++≥? -+-+≤-??≥=? (1)写出其对偶问题;(2)用图解法解对偶问题;(3)利用(2)的结果及根据对偶问 题性质写出原问题的最优解。 解:(1)原问题的对偶问题为: 12 12121212 12max 2322 23.. 35 36 0,0 w y y y y y y s t y y y y y y =--≤??+≤?? -≤??+≤??≥≤? 或者等价变形为: 12 12121212 12max 232223..3536 0,0 w y y y y y y s t y y y y y y =++≤??-≤?? +≤??-≤??≥≥? (2)用图解法求解对偶问题 12 12121212 max 2322 23.. 3536 w y y y y y y s t y y y y =++≤??-≤?? +≤??-≤ 如图示,可行区域为四边形OABC ,最优顶点为B 点,即(1.6,0.2)y * =, 3.8w * =
(3)利用互补松紧定理及(2)的结果求解原问题: 设原问题的最优解为( )1 23 4x x x x x ** ***=。 由于121.60, 0.20y y * * =>=>,故在最优解()12 3 4x x x x x ** * **=处有: 1234 1234232 2330,1,2,3,4j x x x x x x x x x j ******** * ?+++=??-+-+=-??≥=?? 又因对偶问题第4个约束方程为:1.6-0.6=1<6,故40x * =,代入上式得到: 123 123232 230,1,2,3,4j x x x x x x x j ****** * ?++=??-+-=-??≥=?? 原问题有无穷多个最优解。令30x *=得到解为1 1.6x *=,20.2x *= 即()1.60.200x * =, 3.8z * = 2.8题解答见课堂讲解。 2.9 用对偶单纯形法求解下列线性规划问题: (2) 123 123123123min 524324 .. 63510,,0z x x x x x x s t x x x x x x =++++≥?? ++≥??≥? , 解:先将原问题进行标准形化: 1231234123512345max()524324 .. 63510,,,,0 z x x x x x x x s t x x x x x x x x x -=---++-=?? ++-=??≥? 选45,x x 为基变量,并将问题化为: 1231234123512345max()524324 .. 63510,,,,0z x x x x x x x s t x x x x x x x x x -=------+=-?? ---+=-??≥? 列表计算如下:
运筹学典型考试试题及答案
二、计算题(60分) 1、已知线性规划(20分) MaxZ=3X1+4X2 X1+X2≤5 2X1+4X2≤12 3X1+2X2≤8 X1,X2≥0 其最优解为: 基变量X1X2X3X4X5 X33/2 0 0 1 -1/8 -1/4 X25/2 0 1 0 3/8 -1/4 X1 1 1 0 0 -1/4 1/2 σj 0 0 0 -3/4 -1/2 1)写出该线性规划的对偶问题。 2)若C2从4变成5,最优解是否会发生改变,为什么? 3)若b2的量从12上升到15,最优解是否会发生变化,为什么? 4)如果增加一种产品X6,其P6=(2,3,1)T,C6=4该产品是否应该投产?为什么?解: 1)对偶问题为 Minw=5y1+12y2+8y3 y1+2y2+3y3≥3 y1+4y2+2y3≥4 y1,y2≥0 2)当C2从4变成5时, σ4=-9/8 σ5=-1/4 由于非基变量的检验数仍然都是小于0的,所以最优解不变。 3)当若b2的量从12上升到15 X=9/8 29/8 1/4 由于基变量的值仍然都是大于0的,所以最优解的基变量不会发生变化。 4)如果增加一种新的产品,则 P6’=(11/8,7/8,-1/4)T σ6=3/8>0 所以对最优解有影响,该种产品应该生产 2、已知运输问题的调运和运价表如下,求最优调运方案和最小总费用。(共15分)。 B1B2B3产量销地 产地 A1 5 9 2 15 A2 3 1 7 11 A3 6 2 8 20 销量18 12 16 解:初始解为
计算检验数 由于存在非基变量的检验数小于0,所以不是最优解,需调整 调整为: 重新计算检验数 所有的检验数都大于等于0,所以得到最优解 3、某公司要把4个有关能源工程项目承包给4个互不相关的外商投标者,规定每个承包商只能且必须承包一个项目,试在总费用最小的条件下确定各个项目的承包者,总费用为多少?各承包商对工程的报价如表2所示: (15分) 项目 投标者 A B C D 甲 15 18 21 24 乙 19 23 22 18 丙 26 17 16 19 丁 19 21 23 17 答最优解为: X= 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 1 总费用为50 4. 考虑如下线性规划问题(24分) B 1 B 2 B 3 产量/t A 1 15 15 A 2 11 11 A 3 18 1 1 20 销量/t 18 12 16 B 1 B 2 B 3 产量/t A 1 5 13 0 15 A 2 -2 0 0 11 A 3 0 0 20 销量/t 18 12 16 B 1 B 2 B 3 产量/t A 1 15 15 A 2 11 11 A 3 7 12 1 20 销量/t 18 12 16 B 1 B 2 B 3 产量/t A 1 5 13 0 15 A 2 0 2 2 11 A 3 0 0 0 20 销量/t 18 12 16
运筹学作业习题
线性规划建模及单纯形法 思考题 主要概念及内容: 线性规划模型结构(决策变量,约束不等式、等式,目标函数);线性规划标准形式; 可行解、可行集(可行域、约束集),最优解;基、基变量、非基变量、基向量、非基 向量;基本解、基本可行解、可行基、最优基。 复习思考题: 1、线性规划问题的一般形式有何特征? 2、建立一个实际问题的数学模型一般要几步? 3、两个变量的线性规划问题的图解法的一般步骤是什么? 4、求解线性规划问题时可能出现几种结果,哪种结果反映建模时有错误? 5、什么是线性规划的标准型,如何把一个非标准形式的线性规划问题转化成标准形式。 6、试述线性规划问题的可行解、基本解、基本可行解、最优解、最优基本解的概念及它 们之间的相互关系。 7、试述单纯形法的计算步骤,如何在单纯形表上判别问题具有唯一最优解、有无穷多个 最优解、无界解或无可行解。 8、在什么样的情况下采用人工变量法,人工变量法包括哪两种解法? 9、大M 法中,M 的作用是什么?对最小化问题,在目标函数中人工变量的系数取什 么?最大化问题呢? 10、什么是单纯形法的两阶段法?两阶段法的第一段是为了解决什么问题?在怎样的情 况下,继续第二阶段? 作业习题 1、将下列线性规划问题化为标准型 (1)???????≥=--+-≥-+-≤+-++-+=0,,953413223183622453max 4214321432143214321x x x x x x x x x x x x x x x x x x x z (2)???????≤≥=+-+-≥-+--≤--++++=0 ,0,15 2342722351232243min 4214321432143214 321x x x x x x x x x x x x x x x x x x x f 2、(1)求出下列不等式组所定义的多面体的所有基本解和基本可行解(极点): ?????≥≤++-≤++0,,1243263323 21321321x x x x x x x x x (2)对下述线性规划问题找出所有基本解,指出哪些是基本可行解,并确定最优解. ??? ????≥=-=+-+=+++++=)6,,1(00 31024893631223max 61532143213 21K K j x x x x x x x x x x x x x x z j 3、用图解法求解下列线性规划问题
运筹学各章的作业题答案解析
《管理运筹学》各章的作业 ----复习思考题及作业题 第一章绪论 复习思考题 1、从运筹学产生的背景认识本学科研究的内容和意义。 2、了解运筹学的内容和特点,结合自己的理解思考学习的方法和途径。 3、体会运筹学的学习特征和应用领域。 第二章线性规划建模及单纯形法 复习思考题 1、线性规划问题的一般形式有何特征? 2、建立一个实际问题的数学模型一般要几步? 3、两个变量的线性规划问题的图解法的一般步骤是什么? 4、求解线性规划问题时可能出现几种结果,那种结果反映建模时有错误? 5、什么是线性规划的标准型,如何把一个非标准形式的线性规划问题转化成标准形式。 6、试述线性规划问题的可行解、基础解、基础可行解、最优解、最优基础解的概念及它们之间的相互关系。 7、试述单纯形法的计算步骤,如何在单纯形表上判别问题具有唯一最优解、有无穷多个最优解、无界解或无可行解。 8、在什么样的情况下采用人工变量法,人工变量法包括哪两种解法? 9、大M 法中,M 的作用是什么?对最小化问题,在目标函数中人工变量的系数取什么?最大化问题呢? 10、什么是单纯形法的两阶段法?两阶段法的第一段是为了解决什么问题?在怎样的情况下,继续第二阶段? 作业题: 1、把以下线性规划问题化为标准形式: (1) max z= x1-2x2+x3 s.t. x1+x2+x3≤12 2x1+x2-x3≥ 6 -x1+3x2=9 x1, x2, x3≥0 (2) min z= -2x1-x2+3x3-5x4 s.t x1+2x2+4x3-x4≥ 6 2x1+3x2-x3+x4=12 x1+x3+x4≤ 4 x1, x2, x4≥0
运筹学 练习题
案例1,原始问题: 某公司现有三条生产线,由于原有产品出现销售量下降的情况,管理部门决定调整公司的产品线,停产不赢利的产品以释放产能来生产两种新产品。其中,生产甲产品要占用生产线1和生产线3的部分产能,产品乙需要占用生产线2和3的部分产能。管理部门需要考虑下列问题: 1、公司是否应该生产这两种产品 2、若生产,则两种产品的数量如何确定 数据: 运筹小组与管理部门研究后去顶,两种产品的数量如何确定以使产品的总利润最大 因此,需要如下的信息: 1、每条生产线的可得生产能力是多少 2、生产每一单位产品需要每条生产线多少生产能力 3、每种产品的单位利润是多少 生产部门和财务部门经过分析,提出如下数据: 模型: 1、要做出什么决策(决策变量) 2、做出的决策会有哪些条件限制(约束条件) 3、这些决策的全部评价标准是什么(目标函数)
max z=3x1+5x2 st. x1<=4 2x2<=12 3x1+2x2<=18 x1,x2>=0 决策: x1=2,x2=6, z=3600 生产时间信息: 按模型所确定的生产方案需要生产线2和3的所有时间,只有生产线1有2小时的剩余。 1、用单纯形表求解以下线性规划问题 (1)max z=x1-2x2+x3 .x1+x2+x3≤12 2x1+x2-x3≤6 -x1+3x2≤9 x1,x2,x3≥0 解:标准化,将目标函数转变成极小化,引进松弛变量x4,x5,x60,得到:z’ min -x1+2x2-x3 = .x1+x2+x3+x4=12 2x1+x2-x3+x5= 6 -x1+3x2+x6= 9 x1,x2,x3,x4,x5,x6≥0
运筹学第二章课后题
习题 某厂利用A、B两种原料生产甲、乙、丙三种产品,已知单位产品所需的原料、利润及有关数据如表2—3所示。 产品甲产品乙产品丙拥有量原料A63545 原料B34530 单位利润415 (1)求使该厂获利最大的生产计划。 (2)若产品乙、丙的单位利润不变,当产品甲的单位利润在什么范围内变化时,最优解不变 (3)若原料A市场紧缺,除拥有量外一时无法购进,而原料B如数量不足可去市场购买,单价为,问该厂是否应该购买,且以购进多少为宜 解:(1)设产品甲的产量为x1,产品乙的产量为x2,产品丙的产量为x3. 目标函数为:Max z=4 x1 + x2+5 x3 约束条件:. 该线性规划模型为: 答:该厂获利最大的生产计划为产品甲产量为5,产品乙产量为0,产品丙产量为3,总利润为35。 (2)敏感性报告为:
答:如数据显示,产品甲的单位利润变化范围为:。 (3)敏感性报告为: 由敏感性报告显示原料B允许的增量为15,其影子价格为,又因为市场上原料B 单价为,此时,总利润为。 答:该厂可购买15。 习题 已知某工厂计划生产三种产品,各产品需要在设备A、B、C上加工,有关数据如表2—5所示。 产品A产品B产品C每月设备有效台时 设备A8210300 设备B1058400 设备C21310420 单位利润(千元)32 请分别回答下列问题: (1)如何充分发挥设备能力,才能使生产盈利最大 (2)为了增加产量,可借用其他工厂的设备B,若每月可借用60台时,租金为万 元,问借用设备B是否合算 (3)若另有两种新产品(产品4和产品5),其中生产每件新产品4需用设备A、 B、C各12、5、10台时,单位赢利千元;生产每件新产品5需用设备A、B、 C各4、4、12台时,单位赢利千元。如果设备A、B、C台时不增加,分别回答这两种新产品的投资在经济上是否合算 (4)对产品工艺重新进行设计,改进构造。改进后生产每件产品1,需用设备A、 B、C各9、12、4台时,单位赢利千元,问这对原生产计划有何影响
《运筹学》综合练习题
《 运筹学》综合练习题 第一章 线性规划及单纯形法 1、教材43页——44页1.1题 2、教材44页1.4题 3、教材45页1.8题 4、教材46页1.13题 5、教材46页1.14题 6、补充:判断下述说法是否正确 ● LP 问题的可行域是凸集。 ● LP 问题的基本可行解对应可行域的顶点。 ● LP 问题的最优解一定是可行域的顶点,可行域的顶点也一定是最优解。 ● 若LP 问题有两个最优解,则它一定有无穷多个最优解. ● 求解LP 问题时,对取值无约束的自由变量,通常令 "-'=j j j x x x ,其中∶ ≥"' j j x x ,在用单纯形法求得的最优解中,不可能同时出现 "' j j x x . ● 当用两阶段法求解带有大M 的LP 模型时,若第一阶段的最优目标函数值为零,则可 断言原LP 模型一定有最优解。 7、补充:建立模型 (1)某采油区已建有n 个计量站B 1,B 2…B n ,各站目前尚未被利用的能力为b 1,b 2…b n (吨液量/日)。为适应油田开发的需要,规划在该油区打m 口调整井A 1,A 2…A m ,且这些井的位置已经确定。根据预测,调整井的产量分别为a 1,a 2…a m (吨液量/日)。考虑到原有计量站富余的能力,决定不另建新站,而用原有老站分工管辖调整井。按规划要求,每口井只能属于一个计量站。假定A i 到B j 的距离d ij 已知,试确定各调整井与计量站的关系,使新建集输管线总长度最短。 (2)靠近某河流有两个化工厂(见附图),流经第一个工厂的河流流量是每天500万立方米;在两个工厂之间有一条流量为每天200万立方米的支流。第一个工厂每天排放工业污水2万立方米;第二个工厂每天排放工业污水1.4万立方米 。从第一个工厂排出的污水流到第二个工厂之前,有20%可自然净化。根据环保要求,河流中工业污水的含量不应大于0.2%,若这两个工厂都各自处理一部分污水,第一个工厂的处理成本是1000元/万立方米,第二个工厂的处理成本是800元
最全的运筹学复习题及答案78213
最全的运筹学复习题及 答案78213
四、把下列线性规划问题化成标准形式: 2、minZ=2x1-x2+2x3 五、按各题要求。建立线性规划数学模型 1、某工厂生产A、B、C三种产品,每种产品的原材料消耗量、机械台时消耗量以及这些资源的限量,单位产品的利润如下表所示:
根据客户订货,三种产品的最低月需要量分别为200,250和100件,最大月销售量分别为250,280和120件。月销售分别为250 ,280和120件。问如何安排生产计划,使总利润最大。 2、某建筑工地有一批长度为10米的相同型号的钢筋,今要截成长度为3米的钢筋 90根,长度为4米的 钢筋60根,问怎样下料,才能使所使用的原材料最省? 1.某运输公司在春运期间需要24小时昼夜加班工作,需要的人员数量如下表所示:起运时间服务员数 2—6 6—10 10一14 14—18 18—22 22—2 4 8 10 7 12 4 每个工作人员连续工作八小时,且在时段开始时上班,问如何安排,使得既满足以上要求,又使上班人数最少?
五、分别用图解法和单纯形法求解下列线性规划问题.并对照指出单纯形迭代的每一步相 当于图解法可行域中的哪一个顶点。
六、用单纯形法求解下列线性规划问题: 七、用大M法求解下列线性规划问题。并指出问题的解属于哪一类。
八、下表为用单纯形法计算时某一步的表格。已知该线性规划的目标函数为maxZ=5x1+3x2,约束形式为“≤”,X3,X4为松驰变量.表中解代入目标函数后得Z=10 X l X2X3X4 —10 b -1 f g X3 2 C O 1 1/5 X l a d e 0 1 (1)求表中a~g的值 (2)表中给出的解是否为最优解? (1)a=2 b=0 c=0 d=1 e=4/5 f=0 g=-5 (2)表中给出的解为最优解 第四章线性规划的对偶理论 五、写出下列线性规划问题的对偶问题 1.minZ=2x1+2x2+4x3
运筹学 各章习题
思考题、主要概念及内容 1、了解运筹学的分支,运筹学产生的背景、研究的内容和意义。 2、了解运筹学在工商管理中的应用。 3、体会管理运筹学使用相应的计算机软件,注重学以致用的原则。 第二章 思考题、主要概念及内容 图解法、图解法的灵敏度分析 复习题 1. 考虑下面的线性规划问题: max z=2x1+3x2; 约束条件: x1+2x2≤6, 5x1+3x2≤15, x1,x2≥0. (1) 画出其可行域. (2) 当z=6时,画出等值线2x1+3x2=6. (3) 用图解法求出其最优解以及最优目标函数值. 2. 用图解法求解下列线性规划问题,并指出哪个问题具有惟一最优解、无穷多最优解、无界解或无可行解.(1) min f=6x1+4x2; 约束条件: 2x1+x2≥1, 3x1+4x2≥3, x1,x2≥0. (2) max z=4x1+8x2; 约束条件: 2x1+2x2≤10, -x1+x2≥8, x1,x2≥0. (3) max z=3x1-2x2; 约束条件:
2x1+2x2≥4, x1,x2≥0. (4) max z=3x1+9x2; 约束条件: x1+3x2≤22, -x1+x2≤4, x2≤6, 2x1-5x2≤0, x1,x2≥0 3. 将下述线性规划问题化成标准形式: (1) max f=3x1+2x2; 约束条件: 9x1+2x2≤30, 3x1+2x2≤13, 2x1+2x2≤9, x1,x2≥0. (2) min f=4x1+6x2; 约束条件: 3x1-x2≥6, x1+2x2≤10, 7x1-6x2=4, x1,x2≥0. (3) min f=-x1-2x2; 约束条件: 3x1+5x2≤70, -2x1-5x2=50, -3x1+2x2≥30, x1≤0,-∞≤x2≤∞. (提示:可以令x′1=-x1,这样可得x′1≥0.同样可以令x′2-x″2=x2,其中x′2,x″2≥0.可见当x′2≥x″2时,x2≥0;当x′2≤x″2时,x2≤0,即-∞≤x2≤∞.这样原线性规划问题可以化为含有决策变量x′1,x′2,x″2的线性规划问题,这里决策变量x′1,x′2,x″2≥0.) 4. 考虑下面的线性规划问题: min f=11x1+8x2; 约束条件: 10x1+2x2≥20, 3x1+3x2≥18, 4x1+9x2≥36, x1,x2≥0. (1) 用图解法求解. (2) 写出此线性规划问题的标准形式. (3) 求出此线性规划问题的三个剩余变量的值.
运筹学习题解答(chap2)(1)(1)
第二章 对偶问题与灵敏度分析 一、写出下列线性规划的对偶问题 1、P89,2.1(a) 321422m in x x x Z ++= s.t ???????≥=++≤++≥++. ,0,;534;332;2433213213 21321无约束x x x x x x x x x x x x 解:原模型可化为 321422m in x x x Z ++= s.t ????? ??≥=++≥≥++. ,0,;534; 3-3--2-;24332 13 2 1 32132 1321无约束x x x y y y x x x x x x x x x 于是对偶模型为 321532m ax y y y W +-= s.t ???????≥≤+-≤+-≤+-.,0,;4334;243;223213213 21321无约束 y y y y y y y y y y y y 2、P89,2.1(b) 321365m ax x x x Z ++= s.t ???????≤≥≤++≥-+-=++. 0,0,;8374;35;5223213213 21321x x x x x x x x x x x x 无约束 解:令033 ≥-='x x 原模型可化为 3 21365m ax x x x Z '-+=
s.t ????? ??≥'≥≤'+≤'='+. 0,0,; 83-74;3--5-;52-2321 3 21 3213 21321x x x y y y x x x x x x x x x 无约束 于是对偶模型为 321835m in y y y W +-= s.t ???????≥-≥---≥+-=++. 0,,; 332;6752;543213213 21321y y y y y y y y y y y y 无约束 或???????≥≤++≥+-=++.0,,;332; 6752; 54321321321321y y y y y y y y y y y y 无约束 二、灵敏度分析 1、P92, 2.11线性规划问题 213m ax x x Z += s.t ??? ??≥≤+≤+0,1025; 742 12121x x x x x x 最优单纯形表如下 试用灵敏度分析的方法,分析: (1) 目标函数中的系数21,c c 分别在什么范围内变化,最优解不变? (2) 约束条件右端常数项21,b b 分别在什么范围内变化,最优基保持不变? 解:(1) 1c 的分析:要使得最优解不变,则需
(完整版)运筹学》习题答案运筹学答案
《运筹学》习题答案 一、单选题 1.用动态规划求解工程线路问题时,什么样的网络问题可以转化为定步数问题求解()B A.任意网络 B.无回路有向网络 C.混合网络 D.容量网络 2.通过什么方法或者技巧可以把工程线路问题转化为动态规划问题?()B A.非线性问题的线性化技巧 B.静态问题的动态处理 C.引入虚拟产地或者销地 D.引入人工变量 3.静态问题的动态处理最常用的方法是?B A.非线性问题的线性化技巧 B.人为的引入时段 C.引入虚拟产地或者销地 D.网络建模 4.串联系统可靠性问题动态规划模型的特点是()D A.状态变量的选取 B.决策变量的选取 C.有虚拟产地或者销地 D.目标函数取乘积形式 5.在网络计划技术中,进行时间与成本优化时,一般地说,随着施工周期的缩短,直接费用是( )。C A.降低的 B.不增不减的 C.增加的 D.难以估计的 6.最小枝权树算法是从已接接点出发,把( )的接点连接上C A.最远 B.较远 C.最近 D.较近 7.在箭线式网络固中,( )的说法是错误的。D A.结点不占用时间也不消耗资源 B.结点表示前接活动的完成和后续活动的开始 C.箭线代表活动 D.结点的最早出现时间和最迟出现时间是同一个时间 8.如图所示,在锅炉房与各车间之间铺设暖气管最小的管道总长度是( )。C A.1200 B.1400 C.1300 D.1700 9.在求最短路线问题中,已知起点到A,B,C三相邻结点的距离分别为15km,20km,25km,则()。D A.最短路线—定通过A点 B.最短路线一定通过B点 C.最短路线一定通过C点 D.不能判断最短路线通过哪一点 10.在一棵树中,如果在某两点间加上条边,则图一定( )A A.存在一个圈 B.存在两个圈 C.存在三个圈 D.不含圈 11.网络图关键线路的长度( )工程完工期。C A.大于 B.小于 C.等于 D.不一定等于
运筹学习题集(第二章)
判断题 判断正误,如果错误请更正 第二章线形规划的对偶理论 1.原问题第i个约束是<=约束,则对偶变量yi>=0. 2.互为对偶问题,或则同时都有最优解,或则同时都无最优解. 3.原问题有多重解,对偶问题也有多重解. 4.对偶问题有可行解,原问题无可行解,则对偶问题具有无界解. 5.原问题无最优解,则对偶问题无可行解. 6.设X,Y分别为{minZ=CX|AX>=b,X>=0}和{maxw=Yb|YA<=C,Y>=0}的可行解,则有 (1)CX<=Yb; (2)CX是w的上界; (3)当X,Y为最优解,CX=Yb; (4)当CX=Yb 时,有YXs+YsX=0; (5)X为最优解且B是最优基时,则Y=CB-1是最优解; (6)松弛变量Ys的检验数是λs,则X=-λs是基本解,若Ys是最优解, 则X=-λs是最优 解. 7.原问题与对偶问题都可行,则都有最优解. 8.原问题具有无界解,则对偶问题可行. 9.若X,Y是原问题与对偶问题的最优解.则X=Y. 10.若某种资源影子价格为0,则该资源一定有剩余. 11影子价格就是资源的价格. 12.原问题可行对偶问题不可行,可用对偶单纯形法计算. 13.对偶单纯形法比值失效说明原问题具有无界解. 14.对偶单纯形法是直接解对偶问题的一种解法. 15.减少一个约束,目标值不会比原来变差. 16.增加一个约束,目标值不会比原来变好.
17增加一个变量, 目标值不会比原来变差. 18.减少一个非基变量, 目标值不变. 19.当Cj(j=1,2,3,……,n)在允许的最大范围内同时变化时,最优解不变。 选择题 在下列各题中,从4个备选答案中选出一个或从5个备选答案中选出2~5个正确答案。 第二章线性规划的对偶理论 1.如果决策变量数列相等的两个线规划的最优解相同,则两个线性规划 A约束条件相同 B目标函数相同 C最优目标函数值相同 D以上结论都不对 2.对偶单纯形法的最小比值规则是为了保证 A使原问题保持可行 B使对偶问题保持可行 C逐步消除原问题不可行性 D逐步消除对偶问题不可行性 3.互为对偶的两个线性规划问题的解存在关系 A若最优解存在,则最优解相同 B原问题 无可行解,则对偶问题也无可行解 C对偶问题无可行解,原问题可能无可行解 D一个问题无界,则另一个问题无可行解 E一个问题无可行解,则另一个问题具有无界解4.已知规范形式原问题(max)的最优表中的检验数为(λ1,λ2,……λn),松弛变量 的检验数为(λn+1,λn+2,……λn+m),则对偶问题的最优解为 A—(λ1,λ2,…… λn) B (λ1,λ2,……λn) C —(λn+1,λn+2,……λn+m)D(λn+1,λn+2,…… λn+m) 5.原问题与对偶问题都有可行解,则 A原问题有最优解,对偶问题可能没有最优解B原 问题与对偶问题可能都没有最优解 C可能一个问题有最优解,另一个问题具有无界解D 原问题与对偶问题都有最优解 计算题 线性规划问题和对偶问题 对于如下的线性规划问题 min z = 3x 1 + 2x 2 +x 3
《运筹学》习题线性规划部分练习题及答案.doc
《运筹学》线性规划部分练习题 一、思考题 1. 什么是线性规划模型,在模型中各系数的经济意义是什么? 2. 线性规划问题的一般形式有何特征? 3. 建立一个实际问题的数学模型一般要几步? 4. 两个变量的线性规划问题的图解法的一般步骤是什么? 5. 求解线性规划问题时可能出现几种结果,那种结果反映建模时有错误? 6. 什么是线性规划的标准型,如何把一个非标准形式的线性规划问题转化成标准形式。 7. 试述线性规划问题的可行解、基础解、基础可行解、最优解、最优基础解的概念及它们之间的相互关系。 8. 试述单纯形法的计算步骤,如何在单纯形表上判别问题具有唯一最优解、有无穷多个最优解、无界解或无可行解。 9. 在什么样的情况下采用人工变量法,人工变量法包括哪两种解法? 10.大M 法中,M 的作用是什么?对最小化问题,在目标函数中人工变量的系数取什么?最大化问题呢? 11.什么是单纯形法的两阶段法?两阶段法的第一段是为了解决什么问题?在怎样的情况下,继续第二阶段? 二、判断下列说法是否正确。 1. 线性规划问题的最优解一定在可行域的顶点达到。 2. 线性规划的可行解集是凸集。 3. 如果一个线性规划问题有两个不同的最优解,则它有无穷多个最优解。 4. 线性规划模型中增加一个约束条件,可行域的范围一般将缩小,减少一个约束条件,可行域的范围一般将扩大。 5. 线性规划问题的每一个基本解对应可行域的一个顶点。 6. 如果一个线性规划问题有可行解,那么它必有最优解。 7. 用单纯形法求解标准形式(求最小值)的线性规划问题时,与0 >j σ对应的变量都可以被选作换入变量。 8. 单纯形法计算中,如不按最小非负比值原则选出换出变量,则在下一个解中至少有一个基变量的值是负的。 9. 单纯形法计算中,选取最大正检验数k σ对应的变量k x 作为换入变量,可使目 标函数值得到最快的减少。 10. 一旦一个人工变量在迭代中变为非基变量后,该变量及相应列的数字可以从单纯形表中删除,而不影响计算结果。 三、建立下面问题的数学模型 1. 某公司计划在三年的计划期内,有四个建设项目可以投资:项目Ⅰ从第一年到 第三年年初都可以投资。预计每年年初投资,年末可收回本利120% ,每年又可以重新将所获本利纳入投资计划;项目Ⅱ需要在第一年初投资,经过两年可收回本利150% ,又可以重新将所获本利纳入投资计划,但用于该项目的最大投资额不得超过20万元;项目Ⅲ需要在第二年年初投资,经过两年可收回本利160% ,但用于该项目的最大投资额不得超过15万元;项目Ⅳ需要在第三年年初投资,年末可收回本利140% ,但用于该项目的最大投资额不得超过10万元。在这个计划期内,该公司第一年可供投资的资金有30万元。问怎样的投资方案,才能使该公司在这个计划期获得最大利润? 2.某饲养场饲养动物,设每头动物每天至少需要700克蛋白质、30克矿物质、 100克维生素。现有五种饲料可供选用,各种饲料每公斤营养成分含量及单 价如下表2—1所示:
运筹学练习题
《运筹学》--- 数据、模型与决策练习题 2010年9月 一、线性规划:基本概念 1、下面的表格总结了两种产品A和B的关键信息以及生产所需的资源Q, R, S: 满足所有线性规划假设。 (1)在电子表格上为这一问题建立线性规划模型; (2)用代数方法建立一个相同的模型; (3)用图解法求解这个模型。 2、今天是幸运的一天,你得到了10000美元的奖金。除了将4000美元用于交税和请客之外,你决定将剩余的6000美元用于投资。两个朋友听到这个消息后邀请你成为两家不同公司的合伙人,每一个朋友介绍了一家。这两个选择的每一个都将会花去你明年夏天的一些时间并且要花费一些资金。在第一个朋友的公司中成为一个独资人要求投资5000美元并花费400小时,估计利润(不考虑时间价值)是4500美元。第二个朋友的公司的相应数据为4000美元和500小时,估计利润为4500美元。然而每一个朋友都允许你根据所好以任意比例投资。如果你选择投资一定比例,上面所有给出的独资人的数据(资金投资、时间投资和利润)都将乘以一个相同的比例。 因为你正在寻找一个有意义的夏季工作(最多600小时),你决定以能够带来最大总估计利润的组合参与到一个或全部朋友的公司中。你需要解决这个问题,找到最佳组合。 (1)为这一问题建立电子表格模型。找出数据单元格、可变单元格、目标单元格,并且用SUMPRODUCT函数表示每一个输出单元格中的Excel等式。 (2)用代数方法建立一个同样的模型。 (3)分别用模型的代数形式和电子表格形式确定决策变量、目标函数、非负约束、函数约束和参数。 (4)使用图解法求解这个模型。你的总期望利润是多少 3、伟特制窗(Whitt Window)公司是一个只有三个雇员的公司,生产两种手工窗户:木框窗户和铝框窗户。公司每生产一个木框窗户可以获利60美元,一个铝框窗户可以获利30
运筹学作业题
1.已知某线性规划问题的初始单纯形表和用单纯形表法迭代后得到的表1,试求括号中未知数a-l的数值。 解: (1)X5是基变量,检验数l=0 (2)x1是基变量,则,g=1,h=0 (3)x4行乘以1/2得到迭代后的x1行 所以,f=6*1/2=3, b=2,c=4,d=-2 (4)x4行乘以1/2加到x5行上,得到迭代后的x5行 所以,c*1/2+3=i,i=5,d*1/2+e=1, e=2 (5)迭代前为初始单纯形表,价值系数为初始表检验数 所以,x2价值系数为-1,x3价值系数为2,x4价值系数为0 则,-7=-1-(2a-0*i),所以a=3 j=2-(-a)=5;k=0-(1/2*a+1/2*0)=-3/2 即,a=3,b=2,c=4,d=-2,e=2, f=3, g=1, h=0, i=5, j=5, k= -3/2, l=0 2.已知某求极大化线性规划问题用单纯形法求解时的初始单纯形表及最终单纯
解:初始单纯形表中的单位矩阵,在最终单纯形表中变化为B -1 (1) ????????????--=-21043041411 h i l B ????? ?????=????????????????????? ?--==-2/54/254/520152********** 'b h i l b B b 在最终表中,x 4是基变量,所以l =1 所以,b=10,i=-1/4,h=-1/2 (2) ????? ?????=??????????????????????----==-0102121210414304141111'1a p B p 则a=2 (3)???? ??????=??????????????????????----==-1001121210414304141121'2c p B p 则c=3 以此类推其它未知数取值。 即,a=2 b=10 c=3 d=1/4 e=5/4 f=-1/2 g=-3/4 h= -1/2 i= -1/4 j= -1/4 k=0 l=1 3.给出线性规划问题 ???? ? ????=≥≤++ ≤+ + ≤+≤+++++=) 4,...,1(09 66283.42max 3 214 3 2 2 1 42 14 321j x x x x x x x x x x x x st x x x x z j 要求:(1)写出其对偶问题;(2)已知原问题最优解为X*=(2,2,4,0),试根据对偶理论,直接写出对偶问题的最优解。 解:(1)其对偶问题为 ???? ?????=≥≥+≥+ ≥++ +≥+++++=) 4,...,1(01 14322.9668min 3 14 3 432 142 1 4321j y y y y y y y y y y y y st y y y y w j (2)根据对偶理论知,4,2,2321===x x x 均绝对大于零,所以其变量对应的对偶问题
运筹学作业2(清华版第二章部分习题)答案
运筹学作业2(第二章部分习题)答案 2.1 题 (P . 77) 写出下列线性规划问题的对偶问题: (1)123123123123123m ax 224..34223343500,z x x x s t x x x x x x x x x x x x =++? ? ++≥??++≤? ? ++≤? ≥≥??无约束,; 解:根据原—对偶关系表,可得原问题的对偶规划问题为: 123123123123123m ax 235..223424334,0,0w y y y s t y y y y y y y y y y y y =++??++≤??++≤? ?++=? ≥≤≤?? (2)111 1 m in ,1,,,1,,0,1,,;1,,m n ij ij i j n ij ij i j n ij ij j j ij z c x c x a i m c x b j n x i m j n ====?=? ? ? ==????==??≥==??∑∑∑∑ 解:根据原—对偶关系表,可得原问题的对偶规划问题为: 11m ax 1,,;1,,m n i i j j i j i j ij i w a u b v u v c i m j n u ==? =+???+≤? ?==? ??∑∑ j 无约束,v 无约束 2.2判断下列说法是否正确,为什么? (1) 如果线性规划的原问题存在可行解,则其对偶问题也一定存在可行解; 答:错。 因为:若线性规划的原问题存在可行解,且其对偶问题有可行解,则原问题和可行问题都将有最优解。但,现实中肯定有一些问题是无最优解的,故本题说法不对。
例如原问题 12 12212m ax 31..30,0z x x x x s t x x x =++≥??≤? ?≥≥?有可行解,但其对偶问题 12 11212m in 33..10,0w y y y s t y y y y =+≥??+ ≥??≤≥?无可行解。 (2) 如果线性规划的对偶问题无可行解,则原问题也一定无可行解; 答:错,如(1)中的例子。 (3) 在互为对偶的一对原问题与对偶问题中,不管原问题是求极大或求极小,原问题可 行解的目标函数值一定不超过其对偶问题可行解的目标函数值。 答:错。正确说法是:在互为对偶的一对原问题与对偶问题中,求极大的问题可行解的目标函数值一定不超过求极小的问题可行解的目标函数值。 (4) 任何线性规划问题具有唯一的对偶问题。 答:正确。 2.5给出线性规划问题 123 123123123123m ax 221.. 22 0,0,0z x x x x x x x x x s t x x x x x x =+++-≤? ?-+=?? ++≥??≥≥≥? 写出其对偶问题;(2)利用对偶问题性质证明原问题目标函数值1z ≤ 解:(1)原问题的对偶问题为: 123 123123123123m in 22212.. 10,,0w y y y y y y y y y s t y y y y y y =++++≥? ?-+≤?? -++=? ?≥≤?无约束 (2)取()011T y =,既1230,1,0y y y ===,经验证,()011T y =是对偶问题的一个可行解,并且1w =。由对偶问题的性质可得1z w ≤= 2.9 用对偶单纯形法求解下列线性规划问题: (2)123 123123 123m in 524324..63510,,0z x x x x x x s t x x x x x x =++++≥??++≥??≥? ,
